Deck 14: Analysis of Categorical Data
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/158
Play
Full screen (f)
Deck 14: Analysis of Categorical Data
1
Of the values for a chi-square test statistic listed below, which one is likely to lead to rejecting the null hypothesis in a goodness-of-fit test?
A) 0
B) 1.3
C) 1.9
D) 40
A) 0
B) 1.3
C) 1.9
D) 40
D
2
In chi-square tests, there is a rule known as Rule of Five. What does this rule require?
A) It requires that the observed frequency for each cell be five or more.
B) It requires that the degrees of freedom for the test be at least five.
C) It requires that the expected frequency for each cell be five or more.
D) It requires that the difference between the observed and expected frequency for each cell be at least five.
A) It requires that the observed frequency for each cell be five or more.
B) It requires that the degrees of freedom for the test be at least five.
C) It requires that the expected frequency for each cell be five or more.
D) It requires that the difference between the observed and expected frequency for each cell be at least five.
C
3
In a chi-square goodness-of-fit test with 5 degrees of freedom and a significance level of 0.05, the chi-square value from the table is 11.0705. Which of the following computed values of the chi-square test statistic will lead to rejection of the null hypothesis?
A) 7.814
B) 8.952
C) 10.78
D) 17.61
A) 7.814
B) 8.952
C) 10.78
D) 17.61
D
4
Which of the following must be known in order to determine the critical values in the chi-square distribution table?
A) the degrees of freedom
B) the probability of Type I error
C) the probability of Type II error
D) both the degrees of freedom and the probability of Type I error
A) the degrees of freedom
B) the probability of Type I error
C) the probability of Type II error
D) both the degrees of freedom and the probability of Type I error

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following is the appropriate test to use if we wish to determine whether there is evidence that the proportion of successes is higher in group 1 than in group 2?
A) z test
B) test
C) t test with 2 degrees of freedom
D) F test with 2 degrees of freedom
A) z test
B) test
C) t test with 2 degrees of freedom
D) F test with 2 degrees of freedom

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
6
In a goodness-of-fit test, suppose that a sample showed that the observed frequency 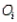 and the expected frequency
and the expected frequency 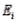 were equal for each cell i. Using this information, what may one conclude about the null hypothesis?
were equal for each cell i. Using this information, what may one conclude about the null hypothesis?
A) It is rejected at0.05 but is not rejected at0.025.
B) It is not rejected at0.05 but is rejected at0.025.
C) It is rejected at any level.
D) It is not rejected at anylevel.
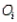 and the expected frequency
and the expected frequency 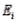 were equal for each cell i. Using this information, what may one conclude about the null hypothesis?
were equal for each cell i. Using this information, what may one conclude about the null hypothesis?A) It is rejected at0.05 but is not rejected at0.025.
B) It is not rejected at0.05 but is rejected at0.025.
C) It is rejected at any level.
D) It is not rejected at anylevel.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
7
In the chi-square goodness-of-fit test, if the expected frequencies, 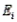 , and the observed frequencies,
, and the observed frequencies, 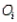 , were very different, what would we conclude?
, were very different, what would we conclude?
A) The null hypothesis is false, and we would reject it.
B) The null hypothesis is true, and we would not reject it.
C) The alternative hypothesis is false, and we would reject it.
D) The chi-square distribution is invalid, and we would use the t-distribution instead.
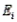 , and the observed frequencies,
, and the observed frequencies, 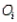 , were very different, what would we conclude?
, were very different, what would we conclude?A) The null hypothesis is false, and we would reject it.
B) The null hypothesis is true, and we would not reject it.
C) The alternative hypothesis is false, and we would reject it.
D) The chi-square distribution is invalid, and we would use the t-distribution instead.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
8
How is a chi-square goodness-of-fit test conducted?
A) as a lower-tailed test
B) as an upper-tailed test
C) as a two-tailed test
D) either as a lower-tailed or as an upper-tailed test
A) as a lower-tailed test
B) as an upper-tailed test
C) as a two-tailed test
D) either as a lower-tailed or as an upper-tailed test

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
9
Consider a multinomial experiment with 200 trials, and the outcome of each trial can be classified into one of five categories. In this case, how many degrees of freedom would be associated with the chi-square goodness-of-fit test?
A) 195
B) 40
C) 5
D) 4
A) 195
B) 40
C) 5
D) 4

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
10
To determine whether a single coin is fair, the coin was tossed 250 times, and heads was observed 140 times. What is the value of the test statistic?
A) 13.6
B) 30
C) 40
D) 110
A) 13.6
B) 30
C) 40
D) 110

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
11
Which of the following best describes the sampling distribution of the test statistic for a goodness-of-fit test with k categories?
A) It is a Student t distribution with k - 1 degrees of freedom.
B) It is a normal distribution.
C) It is a chi-square distribution with k - 1 degrees of freedom.
D) It is an approximately chi-square distribution with k - 1 degrees of freedom.
A) It is a Student t distribution with k - 1 degrees of freedom.
B) It is a normal distribution.
C) It is a chi-square distribution with k - 1 degrees of freedom.
D) It is an approximately chi-square distribution with k - 1 degrees of freedom.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following is NOT a characteristic of a multinomial experiment?
A) The experiment consists of a fixed number, n, of trials.
B) The outcome of each trial can be classified into one of two categories called successes and failures.
C) The probabilitythat the outcome will fall into cell i remain constant for each trial.
D) Each trial of the experiment is independent of the other trials.
A) The experiment consists of a fixed number, n, of trials.
B) The outcome of each trial can be classified into one of two categories called successes and failures.
C) The probabilitythat the outcome will fall into cell i remain constant for each trial.
D) Each trial of the experiment is independent of the other trials.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
13
In a goodness-of-fit test, suppose that the value of the test statistic is 11.89 and the degrees of freedom are 5. At the 5% significance level, what may one conclude about the null hypothesis?
A) It is rejected, and the p-value for the test is smaller than 0.05.
B) It is not rejected, and the p-value for the test is greater than 0.05.
C) It is rejected, and the p-value for the test is greater than 0.05.
D) It is not rejected, and the p-value for the test is smaller than 0.05.
A) It is rejected, and the p-value for the test is smaller than 0.05.
B) It is not rejected, and the p-value for the test is greater than 0.05.
C) It is rejected, and the p-value for the test is greater than 0.05.
D) It is not rejected, and the p-value for the test is smaller than 0.05.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
14
If each element in a population is classified into one and only one of several categories, which of the following best describes this kind of population?
A) It is a normal population.
B) It is a multinomial population.
C) It is a chi-square population.
D) It is a binomial population.
A) It is a normal population.
B) It is a multinomial population.
C) It is a chi-square population.
D) It is a binomial population.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
15
In a goodness-of-fit test, suppose that the value of the test statistic is 13.08 and the number of degrees of freedom is 6. At the 5% significance level, what may one conclude about the null hypothesis?
A) It is rejected, and the p-value for the test is smaller than 0.05.
B) It is not rejected, and the p-value for the test is greater than 0.05.
C) It is rejected, and the p-value for the test is greater than 0.05.
D) It is not rejected, and the p-value for the test is smaller than 0.05.
A) It is rejected, and the p-value for the test is smaller than 0.05.
B) It is not rejected, and the p-value for the test is greater than 0.05.
C) It is rejected, and the p-value for the test is greater than 0.05.
D) It is not rejected, and the p-value for the test is smaller than 0.05.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
16
A left-tailed area in the chi-square distribution equals 0.90. Taking this into consideration, for 7 degrees of freedom, what does the table value equal?
A) 1.68987
B) 2.83311
C) 12.0170
D) 14.0671
A) 1.68987
B) 2.83311
C) 12.0170
D) 14.0671

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
17
Which statistical technique is appropriate when we describe a single population of qualitative data with two or more categories?
A) the z test of the difference between two proportions
B) the chi-square goodness-of-fit test
C) the chi-square test of a contingency table
D) either (a) and (b)
A) the z test of the difference between two proportions
B) the chi-square goodness-of-fit test
C) the chi-square test of a contingency table
D) either (a) and (b)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
18
The area to the right of a chi-square value is 0.05. Given this information, for 9 degrees of freedom, what would be the table value?
A) 3.32511
B) 4.16816
C) 16.9190
D) 19.0228
A) 3.32511
B) 4.16816
C) 16.9190
D) 19.0228

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following is our best option if the expected frequency 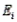 for any cell i is less than five and we want to use Pearson's chi-square statistic in our experiment?
for any cell i is less than five and we want to use Pearson's chi-square statistic in our experiment?
A) We must choose another sample of five or more observations.
B) We should use the normal distribution instead of the chi-square distribution.
C) We should combine the cells such that each observed frequencyis five or more.
D) We increase the number of degrees of freedom for the test by five.
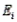 for any cell i is less than five and we want to use Pearson's chi-square statistic in our experiment?
for any cell i is less than five and we want to use Pearson's chi-square statistic in our experiment?A) We must choose another sample of five or more observations.
B) We should use the normal distribution instead of the chi-square distribution.
C) We should combine the cells such that each observed frequencyis five or more.
D) We increase the number of degrees of freedom for the test by five.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
20
Consider a cell in a contingency table. Given the cell's row total of 80, the cell's column total of 60, and a sample size of 250, what is the cell's expected frequency?
A) 1.786
B) 3.125
C) 19.2
D) 20.0
A) 1.786
B) 3.125
C) 19.2
D) 20.0

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
21
If we wanted to conduct a two-tailed test of a population proportion, which of these tests could we employ?
A) z test of a population proportion
B) the chi-square goodness-of-fit test since
C) the chi-square test of independence
D) both a and b
A) z test of a population proportion
B) the chi-square goodness-of-fit test since
C) the chi-square test of independence
D) both a and b

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
22
What summary data does a contingency table contain?
A) It classifies data with respect to two qualitative variables.
B) It divides each variable into two or more categories.
C) It contains numbers that show the frequency of occurrence of all possible combinations of categories.
D) All of (a), (b), and (c).
A) It classifies data with respect to two qualitative variables.
B) It divides each variable into two or more categories.
C) It contains numbers that show the frequency of occurrence of all possible combinations of categories.
D) All of (a), (b), and (c).

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
23
What is the appropriate test to use if we wish to determine whether there is evidence that the proportion of successes is the same in group 1 as in group 2?
A) the z test
B) thetest
C) the z test and thetest
D) t test with 2 degrees of freedom
A) the z test
B) thetest
C) the z test and thetest
D) t test with 2 degrees of freedom

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
24
Which statistical technique is appropriate when we wish to analyze the relationship between two qualitative variables with two or more categories?
A) the chi-square test of a multinomial experiment
B) the chi-square test of a contingency table
C) the t test of the difference between two means
D) the z test of the difference between two proportions
A) the chi-square test of a multinomial experiment
B) the chi-square test of a contingency table
C) the t test of the difference between two means
D) the z test of the difference between two proportions

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
25
Consider a cell in a contingency table. Given the cell's row total of 200, the cell's column total of 75, and a sample size of 1000, what is the cell's expected frequency?
A) 10
B) 15
C) 20
D) 44
A) 10
B) 15
C) 20
D) 44

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
26
Which of the following statements is NOT a characteristic of a goodness-of-fit test?
A) It determines the likelihood that sample data have been generated from a population that conforms to a specified type of probability distribution.
B) It compares the entire shapes of two (discrete or continuous) probability distributions: one describing known population data and the other one describing hypothetical sample data.
C) The aim of the test might be limited to identifying only the family to which the underlying distribution belongs.
D) The aim of the test might be limited to identifying only the family to which the underlying distribution belongs or it might go further, seeking even to identify a particular member of that family.
A) It determines the likelihood that sample data have been generated from a population that conforms to a specified type of probability distribution.
B) It compares the entire shapes of two (discrete or continuous) probability distributions: one describing known population data and the other one describing hypothetical sample data.
C) The aim of the test might be limited to identifying only the family to which the underlying distribution belongs.
D) The aim of the test might be limited to identifying only the family to which the underlying distribution belongs or it might go further, seeking even to identify a particular member of that family.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
27
Which of the following statements is NOT a property of a contingency table test?
A) The nature of the sampling distribution of chi-square depends on the number of degrees of freedom associated with the under investigation.
B) The degrees of freedom are found as (r - 2)(c - 2), where r represents number of rows and c represents number of columns.
C) The contingency table must have a minimum of two rows and two columns.
A) The nature of the sampling distribution of chi-square depends on the number of degrees of freedom associated with the under investigation.
B) The degrees of freedom are found as (r - 2)(c - 2), where r represents number of rows and c represents number of columns.
C) The contingency table must have a minimum of two rows and two columns.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
28
If we wanted to conduct a one-tailed test of a population proportion, which of the following tests could we employ?
A) z test of a population proportion
B) the chi-square goodness-of-fit test since
C) the chi-square test of independence
A) z test of a population proportion
B) the chi-square goodness-of-fit test since
C) the chi-square test of independence

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
29
A chi-square test of a contingency table with 4 rows and 5 columns shows that the value of the test statistic is 22.18. Which of the following is the most accurate statement that can be made about the p-value for this test?
A) p-value is greater than 0.05
B) p-value is smaller than 0.025
C) p-value is greater than 0.025 but smaller than 0.05
D) p-value is greater than 0.10
A) p-value is greater than 0.05
B) p-value is smaller than 0.025
C) p-value is greater than 0.025 but smaller than 0.05
D) p-value is greater than 0.10

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
30
How many columns would the table associated with a contingency table test with 4 rows and 15 degrees of freedom have?
A) 5 columns
B) 6 columns
C) 9 columns
D) 11 columns
A) 5 columns
B) 6 columns
C) 9 columns
D) 11 columns

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
31
Which of the following procedures would be considered a suitable application for the chi-square technique?
A) testing the alleged independence of two qualitative variables
B) making inferences about the relative sizes of more than two population proportions
C) conducting a goodness-of-fit-test to determine whether data are consistent with data drawn from a particular probability distribution
A) testing the alleged independence of two qualitative variables
B) making inferences about the relative sizes of more than two population proportions
C) conducting a goodness-of-fit-test to determine whether data are consistent with data drawn from a particular probability distribution

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
32
In a chi-square test of independence, the value of the test statistic was  , and the critical value at
, and the critical value at 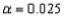 was 11.1433. Which of the following conclusions may we draw from this information?
was 11.1433. Which of the following conclusions may we draw from this information?
A) We fail to reject the null hypothesis at.
B) We reject the null hypothesis at.
C) We don't have enough evidence to accept or reject the null hypothesis at.
D) We should decrease the level of significance in order to reject the null hypothesis.
 , and the critical value at
, and the critical value at 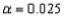 was 11.1433. Which of the following conclusions may we draw from this information?
was 11.1433. Which of the following conclusions may we draw from this information?A) We fail to reject the null hypothesis at.
B) We reject the null hypothesis at.
C) We don't have enough evidence to accept or reject the null hypothesis at.
D) We should decrease the level of significance in order to reject the null hypothesis.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
33
The president of a large university collected data from students concerning building a new library, and classified the responses into different categories (strongly agree, agree, undecided, disagree, strongly disagree) and according to whether the student was male or female. To determine whether the data provide sufficient evidence to indicate that the responses depend upon gender, which of the following would be the most appropriate test?
A) a chi-square goodness-of-fit test
B) a chi-square test of a contingency table (test of independence)
C) a chi-square test of normality
D) a chi-square test of abnormality
A) a chi-square goodness-of-fit test
B) a chi-square test of a contingency table (test of independence)
C) a chi-square test of normality
D) a chi-square test of abnormality

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
34
A chi-square test of independence is applied to a contingency table with four rows and five columns for two qualitative variables. What are the degrees of freedom for this test?
A) 20
B) 16
C) 15
D) 12
A) 20
B) 16
C) 15
D) 12

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
35
Upon which of the following types of variables is the chi-square test of a contingency table based?
A) two qualitative variables
B) two quantitative variables
C) three or more qualitative variables
D) three or more quantitative variables
A) two qualitative variables
B) two quantitative variables
C) three or more qualitative variables
D) three or more quantitative variables

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
36
How many columns does the table associated with a contingency table test with 4 rows and 30 degrees of freedom have?
A) 7 columns
B) 9 columns
C) 11 columns
D) 13 columns
A) 7 columns
B) 9 columns
C) 11 columns
D) 13 columns

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
37
Upon which of the following kinds of variables is the chi-square test of independence based?
A) two qualitative variables
B) two quantitative variables
C) three or more qualitative variables
D) three or more quantitative variables
A) two qualitative variables
B) two quantitative variables
C) three or more qualitative variables
D) three or more quantitative variables

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
38
Which of the following is the number of degrees of freedom for a contingency table with six rows and six columns?
A) 36
B) 25
C) 12
D) 6
A) 36
B) 25
C) 12
D) 6

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
39
A chi-square test of independence with 10 degrees of freedom results in a test statistic of 19.25. Using the chi-square table, which of the following is the most accurate statement that can be made about the p-value for this test?
A) p-value < 0.025
B) 0.025 < p-value < 0.05
C) 0.05 < p-value < 0.10
D) 0.10 < p-value < 0.20
A) p-value < 0.025
B) 0.025 < p-value < 0.05
C) 0.05 < p-value < 0.10
D) 0.10 < p-value < 0.20

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
40
In which of the following situations are contingency tables used?
A) to test independence of two samples
B) to test dependence in matched pairs
C) to test independence of two qualitative variables in a population
D) to describe a single population
A) to test independence of two samples
B) to test dependence in matched pairs
C) to test independence of two qualitative variables in a population
D) to describe a single population

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
41
The rejection region of the chi-square goodness-of-fit test has k - 1 degrees of freedom, where k is the number of categories (called cells).

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
42
A multinomial experiment, where the outcome of each trial can be classified into one of two categories, is identical to a binomial experiment.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
43
A right-tailed area in the chi-square distribution equals 0.05. For 6 degrees of freedom the table value equals 12.5916.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
44
A chi-square goodness-of-fit test with 3 degrees of freedom results in a test statistic of 6.789. Using the chi-square table, the most accurate statement that can be made about the p-value for this test is that 0.05 < p-value < 0.10.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
45
If the test statistic for a chi-square goodness-of-fit test is larger than the critical value, the null hypothesis should be rejected.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
46
Whenever the expected frequency of a cell is less than five, one remedy for this condition is to increase the significance level.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
47
A left-tailed area in the chi-square distribution equals 0.10. For 5 degrees of freedom the table value equals 9.23635.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
48
A goodness-of-fit test determines the likelihood that sample data have been generated from a population that conforms to a specified type of probability distribution.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
49
The rejection region of the chi-square goodness-of-fit test is 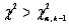 , where k is the number of categories and
, where k is the number of categories and 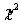 is the value of the test statistics.
is the value of the test statistics.
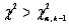 , where k is the number of categories and
, where k is the number of categories and 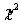 is the value of the test statistics.
is the value of the test statistics.
Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
50
A chi-square goodness-of-fit test is always conducted as a two-tailed test.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
51
For a chi-square distributed random variable with 10 degrees of freedom and a level of significance of 0.025, the chi-square table value is 20.4831. The computed value of the test statistics is 16.857. This will lead us to reject the null hypothesis.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
52
The chi-square goodness-of-fit test involves two categorical variables.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
53
The degrees of freedom associated with a goodness-of-fit test equal the number of rows times the number of columns in the table.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
54
The middle 0.95 portion of the chi-square distribution with 9 degrees of freedom has table values of 3.32511 and 16.9190, respectively.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
55
When the expected cell frequencies are smaller than five, the cells should be combined in a meaningful way such that the expected cell frequencies exceed five.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
56
Whenever the expected frequency of a cell is less than five, one remedy for this condition is to increase the size of the sample.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
57
Whenever the expected frequency of a cell is less than five, one remedy for this condition is to decrease the size of the sample.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
58
The area to the right of a chi-square value is 0.01. For 8 degrees of freedom, the table value is 1.64648.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
59
In applying the chi-square goodness-of-fit test, the rule of thumb for all expected frequencies is that each expected frequency is five or more.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
60
A chi-square goodness-of-fit test is always conducted as a two-tailed test.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
61
Chi-square tests of independence are always lower-tailed because a perfect fit between 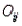 and
and 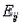 makes the test statistic
makes the test statistic 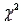 equal to 0.
equal to 0.
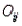 and
and 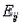 makes the test statistic
makes the test statistic 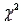 equal to 0.
equal to 0.
Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
62
The degrees of freedom associated with a chi-square test of independence where data are summarized in a contingency table with r rows and c columns equal the number of rows times the number of columns in the table; that is, rc.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
63
In a typical chi-square test of independence, we calculate each expected cell frequency ( 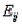 ) as the product of row total (
) as the product of row total ( 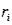 ) times column total (
) times column total ( 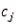 ) times sample size (n).
) times sample size (n).
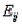 ) as the product of row total (
) as the product of row total ( 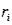 ) times column total (
) times column total ( 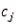 ) times sample size (n).
) times sample size (n).
Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
64
By combining cells that have expected frequencies smaller than five, we guard against having an inflated test statistic that could have led us to incorrectly accept the null hypothesis.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
65
In a typical contingency table test, we calculate each expected cell frequency as the product of row total times column total times sample size.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
66
The degrees of freedom associated with a contingency table test of independence equal the number of rows times the number of columns in the table.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
67
A contingency table classifies data according to two or more categories associated with each of two qualitative variables that are statistically independent of one another.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
68
Numbers in a contingency table show the frequency of occurrence of all possible combinations of categories.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
69
A chi-square test for independence is applied to a contingency table with four rows and four columns for two qualitative variables. The degrees of freedom for this test must be 9.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
70
A contingency table classifies data with respect to two qualitative variables that are each divided into two or more categories.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
71
To be valid, a chi-square test of independence requires that each expected frequency equal 30 or more.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
72
The chi-square test statistic for a contingency table with r rows and c columns can be negative if r is much smaller than
c.
c.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
73
To be valid, a chi-square test of independence requires that the expected frequency for each cell in the contingency table equals ten or more.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
74
In a chi-square test of independence with 6 degrees of freedom and a level of significance of 0.05, the critical value from the chi-square table is 12.5916. The computed value of the test statistics is 11.264. This will lead us to reject the null hypothesis.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
75
A chi-square test for independence is applied to a contingency table with three rows and five columns for two qualitative variables. The degrees of freedom for this test is 8.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
76
A chi-square test for independence is applied to a contingency table with three rows and four columns for two qualitative variables. The degrees of freedom for this test must be 12.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
77
In a chi-square test of independence, the value of the test statistic was 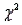 = 15.652, and the critical value at
= 15.652, and the critical value at 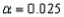 was 11.1433. Thus, we must reject the null hypothesis at
was 11.1433. Thus, we must reject the null hypothesis at 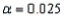 .
.
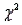 = 15.652, and the critical value at
= 15.652, and the critical value at 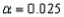 was 11.1433. Thus, we must reject the null hypothesis at
was 11.1433. Thus, we must reject the null hypothesis at 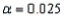 .
.
Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
78
Numbers in a contingency table show the frequency of occurrence of all possible combinations of categories.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
79
Chi-square tests of independence are always lower-tailed because a perfect fit between 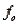 and
and 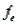 makes
makes 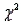 equal to 0.
equal to 0.
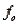 and
and 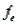 makes
makes 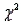 equal to 0.
equal to 0.
Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
80
A chi-square test for independence with 10 degrees of freedom results in a test statistic of 17.894. Using the chi-square table, the most accurate statement that can be made about the p-value for this test is that 0.05 < p-value < 0.10.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck


