Deck 11: A: The Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/136
Play
Full screen (f)
Deck 11: A: The Analysis of Variance
1
What is the term for an experimental plan that creates one treatment group for each treatment, and then randomly assigns each experimental unit to one of these groups?
A) a completely randomized design
B) a randomized block design
C) a matched-pairs design
D) either a or b
A) a completely randomized design
B) a randomized block design
C) a matched-pairs design
D) either a or b
A
2
Which of the following is used as the test statistic of the single-factor ANOVA?
A) Sum of squares for treatments/Sum of squares for error
B) Sum of squares for error/Sum of squares for treatments
C) Mean square for treatments/Mean square for error
D) Mean square for error/Mean square for treatments
A) Sum of squares for treatments/Sum of squares for error
B) Sum of squares for error/Sum of squares for treatments
C) Mean square for treatments/Mean square for error
D) Mean square for error/Mean square for treatments
C
3
Which of the following correctly describes the treatment sum of squares in one-way ANOVA?
A) It equals the sum of the squared deviations between each treatment sample mean and the grand mean, multiplied by the number of observations made for each treatment.
B) It equals the sum of the square deviations between each block sample mean and the grand mean, multiplied by the number of observations made for each block, multiplied by the number of observations per cell.
C) It equals the number of rows (or columns) multiplied by the sum of the squared deviations of the column-block sample means from the grand mean.
D) It equals the number of columns (or rows) multiplied by the sum of the squared deviations of the row-block sample means from the grand mean.
A) It equals the sum of the squared deviations between each treatment sample mean and the grand mean, multiplied by the number of observations made for each treatment.
B) It equals the sum of the square deviations between each block sample mean and the grand mean, multiplied by the number of observations made for each block, multiplied by the number of observations per cell.
C) It equals the number of rows (or columns) multiplied by the sum of the squared deviations of the column-block sample means from the grand mean.
D) It equals the number of columns (or rows) multiplied by the sum of the squared deviations of the row-block sample means from the grand mean.
A
4
Which of the following values may be analyzed using one-way ANOVA?
A) the difference between more than two population means
B) the difference between two population variances
C) the difference between two sample means
D) the difference between two sample population proportions
A) the difference between more than two population means
B) the difference between two population variances
C) the difference between two sample means
D) the difference between two sample population proportions

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following are underlying assumptions in order for an ANOVA completely randomized design to be used?
A) The ANOVA test assumes that the sampled populations are F-distributed.
B)
B) The ANOVA test assumes that the sampled populations have a common variances.
C) The ANOVA test assumes that the samples are randomly selected from their respective populations but they need not be independent.
D) both a and
A) The ANOVA test assumes that the sampled populations are F-distributed.
B)
B) The ANOVA test assumes that the sampled populations have a common variances.
C) The ANOVA test assumes that the samples are randomly selected from their respective populations but they need not be independent.
D) both a and

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
6
In a one-way ANOVA, if the null hypothesis is 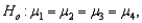 then what would the alternative hypothesis be?
then what would the alternative hypothesis be?
A) at least one of the means is different from the others.
B) at least two of the means are different from the others.
C) at least three of the means are different from the others.
D) all populations means differ.
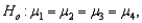 then what would the alternative hypothesis be?
then what would the alternative hypothesis be?A) at least one of the means is different from the others.
B) at least two of the means are different from the others.
C) at least three of the means are different from the others.
D) all populations means differ.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following is equal to the test statistic of the completely randomized ANOVA design?
A) Sum of squares for treatments/Sum of squares for error
B) Sum of squares for error/Sum of squares for treatments
C) Mean square for treatments/Mean square for error
D) Mean square for error/Mean square for treatments
A) Sum of squares for treatments/Sum of squares for error
B) Sum of squares for error/Sum of squares for treatments
C) Mean square for treatments/Mean square for error
D) Mean square for error/Mean square for treatments

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
8
In a one-way ANOVA, if 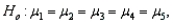 and a sample of size 25 is selected at random from each of the 5 populations, then which of the following is the correct critical value at
and a sample of size 25 is selected at random from each of the 5 populations, then which of the following is the correct critical value at 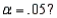
A) z = 1.645
B) t = 2.1318
C) F = 2.45
D) = 9.488
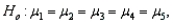 and a sample of size 25 is selected at random from each of the 5 populations, then which of the following is the correct critical value at
and a sample of size 25 is selected at random from each of the 5 populations, then which of the following is the correct critical value at 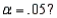
A) z = 1.645
B) t = 2.1318
C) F = 2.45
D) = 9.488

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
9
How many degrees of freedom are there for a denominator in a one-way ANOVA test that includes three population means with ten observations sampled from each population?
A) 30
B) 27
C) 13
D) 12
A) 30
B) 27
C) 13
D) 12

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
10
In a completely randomized design for ANOVA, the number of degrees of freedom for the numerator and denominator for test statistic are 3 and 16, respectively. Which of the following is equal to the total number of observations?
A) 48
B) 32
C) 20
D) 19
A) 48
B) 32
C) 20
D) 19

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
11
In a one-way ANOVA test, the test statistic is F = 4.25. The rejection region is F > 3.06 for the 5% level of significance, F > 3.8 for the 2.5% level, and F > 4.89 for the 1% level. For this test, which of the following is a valid statement about the approximate p-value?
A) It is greater than 0.05.
B) It is between 0.025 and 0.05.
C) It is between 0.01 and 0.025.
D) It is approximately 0.05.
A) It is greater than 0.05.
B) It is between 0.025 and 0.05.
C) It is between 0.01 and 0.025.
D) It is approximately 0.05.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following correctly describes the F statistic for the completely randomized design?
A) It equals the ratio of mean squares for treatments (MST) to mean squares for error (MSE).
B) It equals the ratio of sum of squares for treatments (SST) to sum squares for error (SSE).
C) It equals the ratio of sum of squares for treatments (SST) to total sum of squares (Total SS).
D) It equals the ratio of sum of squares for error (SSE) to total sum of squares (Total SS).
A) It equals the ratio of mean squares for treatments (MST) to mean squares for error (MSE).
B) It equals the ratio of sum of squares for treatments (SST) to sum squares for error (SSE).
C) It equals the ratio of sum of squares for treatments (SST) to total sum of squares (Total SS).
D) It equals the ratio of sum of squares for error (SSE) to total sum of squares (Total SS).

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following is the distribution of the test statistic for analysis of variance?
A) the normal distribution
B) the Student's t distribution
C) the F distribution
D) the binomial distribution
A) the normal distribution
B) the Student's t distribution
C) the F distribution
D) the binomial distribution

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
14
In one-way ANOVA, suppose that there are four treatments with 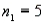 ,
, 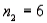 ,
, 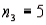 , and
, and 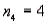 . What is the rejection region for this test at the 5% level of significance?
. What is the rejection region for this test at the 5% level of significance?
A) F >
B) F >
C) F >
D) F >
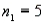 ,
, 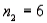 ,
, 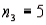 , and
, and 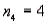 . What is the rejection region for this test at the 5% level of significance?
. What is the rejection region for this test at the 5% level of significance?A) F >
B) F >
C) F >
D) F >

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
15
In one-way ANOVA, which of the following statistics is used to measure the amount of total variation that is unexplained?
A) the sum of squares for treatments
B) the sum of squares for error
C) the total sum of squares
D) the degrees of freedom
A) the sum of squares for treatments
B) the sum of squares for error
C) the total sum of squares
D) the degrees of freedom

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following is a characteristic of all members of the F distribution family?
A) positively skewed between values ofand
B) positively skewed between values of 0 and
C) negatively skewed between values ofand 0
D) both b and c, which is why the normal distribution is a special case of the F-distribution family
A) positively skewed between values ofand
B) positively skewed between values of 0 and
C) negatively skewed between values ofand 0
D) both b and c, which is why the normal distribution is a special case of the F-distribution family

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
17
In one-way ANOVA, suppose that there are three treatments with 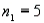 ,
, 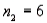 , and
, and 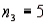 . What is the rejection region for this test at the 5% level of significance?
. What is the rejection region for this test at the 5% level of significance?
A) F > 3.24
B) F > 3.63
C) F > 3.81
D) F > 4.08
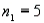 ,
, 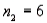 , and
, and 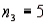 . What is the rejection region for this test at the 5% level of significance?
. What is the rejection region for this test at the 5% level of significance?A) F > 3.24
B) F > 3.63
C) F > 3.81
D) F > 4.08

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
18
In the completely randomized design of ANOVA where there are k treatments and n observations, what are the degrees of freedom for the F statistic?
A) n and k
B) k and n
C) n - k and k - 1
D) k - 1 and n - k
A) n and k
B) k and n
C) n - k and k - 1
D) k - 1 and n - k

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
19
In one-way ANOVA, what is the sum of the squared deviations of each individual sample observation (regardless of the sample to which it belongs) from the mean of all observations?
A) the F statistic
B) the total sum of squares
C) the grand mean
D) the unexplained variance
A) the F statistic
B) the total sum of squares
C) the grand mean
D) the unexplained variance

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following is NOT a required condition for one-way ANOVA?
A) The populations must be normally distributed.
B) The sample sizes must be equal.
C) The population variances must be equal.
D) The samples must be selected randomly and independently from their respective populations.
A) The populations must be normally distributed.
B) The sample sizes must be equal.
C) The population variances must be equal.
D) The samples must be selected randomly and independently from their respective populations.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
21

Refer to ANOVA table one. In this case, how many treatments are there?
A) 13
B) 12
C) 5
D) 3

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
22
In a randomized block design of ANOVA, which of the following correctly describes the number of degrees of freedom associated with the sum of squares for treatments?
A) one less than the total number of observations in all samples
B) one less than the number of blocks
C) one less than the number of populations involved
A) one less than the total number of observations in all samples
B) one less than the number of blocks
C) one less than the number of populations involved

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
23

Refer to ANOVA table one. In a completely randomized design for ANOVA, the numerator and denominator degrees of freedom for the test statistic are 4 and 25, respectively. What must the total number of observations equal?
A) 24
B) 25
C) 29
D) 30

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
24
Which of the following correctly describes Tukey's method of paired comparisons?
A) It is a statistical technique designed to test whether the means of more than two quantitative populations are equal.
B) It is a method employed as a follow-up to ANOVA that seeks out honestly significant differences between paired sample means.
C) It is a method to determine whether different statistical populations have equal variances.
D) It is a method to measure a statistical test's sensitivity to any breach of ANOVA basic assumptions.
A) It is a statistical technique designed to test whether the means of more than two quantitative populations are equal.
B) It is a method employed as a follow-up to ANOVA that seeks out honestly significant differences between paired sample means.
C) It is a method to determine whether different statistical populations have equal variances.
D) It is a method to measure a statistical test's sensitivity to any breach of ANOVA basic assumptions.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
25
The equation: "Total SS = SST + SSB + SSE" applies to which ANOVA model?
A) one-way ANOVA
B) a two-factor factorial design
C) completely randomized design
D) randomized block design
A) one-way ANOVA
B) a two-factor factorial design
C) completely randomized design
D) randomized block design

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
26
For which of the following departures from the conditions required for a completely randomized design is the procedure no longer considered to be robust?
A) The populations are not normally distributed.
B) The population variances are not equal.
C) The samples are not independent.
A) The populations are not normally distributed.
B) The population variances are not equal.
C) The samples are not independent.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
27
A one-way ANOVA test is performed on three independent samples with 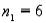 ,
, 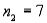 , and
, and 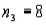 . What is the critical value obtained from the F-table for this test at the 2.5% level of significance?
. What is the critical value obtained from the F-table for this test at the 2.5% level of significance?
A) 3.55
B) 4.56
C) 29.45
D) 39.45
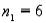 ,
, 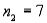 , and
, and 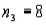 . What is the critical value obtained from the F-table for this test at the 2.5% level of significance?
. What is the critical value obtained from the F-table for this test at the 2.5% level of significance?A) 3.55
B) 4.56
C) 29.45
D) 39.45

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
28
What is an analysis of variance that controls extraneous factors by using the randomized block design?
A) one-way ANOVA
B) two-way ANOVA
C) three-way ANOVA
D) four-way ANOVA
A) one-way ANOVA
B) two-way ANOVA
C) three-way ANOVA
D) four-way ANOVA

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
29
In a randomized block design of ANOVA, how many factors are there to be analyzed?
A) one factor
B) two factors
C) three factors
D) four or more factors
A) one factor
B) two factors
C) three factors
D) four or more factors

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
30
The analysis of variance is a procedure that allows statisticians to compare two or more of which of the following population parameters?
A) means
B) proportions
C) variances
D) standard deviations
A) means
B) proportions
C) variances
D) standard deviations

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
31
The F-test of the randomized block design of the analysis of variance requires that the random variable of interest must be normally distributed and the population variances must be equal. When the random variable is NOT normally distributed, which of the following tests may we use?
A) one-way ANOVA
B) two-way ANOVA
C) chi-square test
D) Friedman test
A) one-way ANOVA
B) two-way ANOVA
C) chi-square test
D) Friedman test

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
32
Which of the following is NOT a property of Tukey's Multiple Comparison Method?
A) It is based on the studentized range statistic q to obtain the critical value needed to construct individual confidence intervals.
B) It requires that all sample sizes are equal, or at least similar.
C) It can be used instead of the analysis of variance.
D) It puts no restriction on the sample means.
A) It is based on the studentized range statistic q to obtain the critical value needed to construct individual confidence intervals.
B) It requires that all sample sizes are equal, or at least similar.
C) It can be used instead of the analysis of variance.
D) It puts no restriction on the sample means.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
33

How many degrees of freedom are there for the denominator in a one-way ANOVA test involving 4 population means with 15 observations sampled from each population?
A) 60
B) 56
C) 45
D) 19

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
34
In the randomized block design for ANOVA, which of the following statements is NOT a property of blocks variation?
A) It equals the sum of the squared deviations between each block sample mean and the grand mean.
B) It measures the variation among block sample means, which is attributable not to chance but to inherent differences among blocks of experimental units.
C) In two-way ANOVA, it equals the blocks mean square.
A) It equals the sum of the squared deviations between each block sample mean and the grand mean.
B) It measures the variation among block sample means, which is attributable not to chance but to inherent differences among blocks of experimental units.
C) In two-way ANOVA, it equals the blocks mean square.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
35
Why would you use the Tukey multiple comparison?
A) to test for normality
B) to test for homogeneity of variance
C) to test independence of errors
D) to test for differences in pairwise means
A) to test for normality
B) to test for homogeneity of variance
C) to test independence of errors
D) to test for differences in pairwise means

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
36
In an ANOVA test, the test statistic is F = 6.75. The rejection region is F > 3.97 for the 5% level of significance, F > 5.29 for the 2.5% level, and F > 7.46 for the 1% level. For this test, what is the p-value?
A) greater than 0.05
B) approximately 0.05
C) between 0.025 and 0.05
D) between 0.01 and 0.025
A) greater than 0.05
B) approximately 0.05
C) between 0.025 and 0.05
D) between 0.01 and 0.025

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
37
In the randomized block design for ANOVA where k is the number of treatments and b is the number of blocks, the degrees of freedom for error are given by which of the following expressions?
A) bk - 1
B) kb + 1
C) (b - 1)(k - 1)
D) k + b - 1
A) bk - 1
B) kb + 1
C) (b - 1)(k - 1)
D) k + b - 1

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
38

Refer to ANOVA table one. A one-way ANOVA test is applied to three independent samples having means 10, 13, and 18, respectively. If each observation in the third sample were increased by 30, how would this affect the value of the F-statistics?
A) They would increase.
B) They would decrease.
C) They would remain unchanged.
D) They would increase by exactly 30.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
39

Refer to ANOVA table two. In the table above, what are the respective numerator and denominator degrees of freedom (identified by asterisks)?
A) 3 and 16
B) 4 and 15
C) 15 and 4
D) 16 and 3

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
40
A professor of statistics in Simon Fraser University wants to determine whether the average starting salaries among graduates of the nine universities in British Columbia are equal. A sample of 25 recent graduates from each university was randomly taken. The appropriate critical value for the ANOVA test is obtained from the F-distribution. What are the respective numbers of degrees of freedom for this distribution?
A) 8 and 216
B) 9 and 25
C) 25 and 15
D) 360 and 14
A) 8 and 216
B) 9 and 25
C) 25 and 15
D) 360 and 14

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
41
One of the assumptions underlying analysis of variance for a completely randomized design is that the observations within each population are normally distributed with unequal variance.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
42
When the effect of a level for one factor depends on which level of another factor is present, what is the most appropriate ANOVA design to use in this situation?
A) one-way ANOVA
B) two-way ANOVA
C) randomized block design
D) matched pairs design
A) one-way ANOVA
B) two-way ANOVA
C) randomized block design
D) matched pairs design

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
43
The randomized block design with exactly two treatments is equivalent to which of the following two-tailed tests?
A) independent samples z-test
B) independent samples equal-variances t-test
C) independent samples unequal-variances t-test
D) matched pairs t-test
A) independent samples z-test
B) independent samples equal-variances t-test
C) independent samples unequal-variances t-test
D) matched pairs t-test

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
44
In a two-way ANOVA, where a is the number of factor A levels and b is the number of factor B levels, which of the following expressions gives the number of the degrees of freedom for the "error term"?
A) (a - 1)(b - 1)
B) n - ab
C) (a - 1) + (b - 1)
D) abn + 1
A) (a - 1)(b - 1)
B) n - ab
C) (a - 1) + (b - 1)
D) abn + 1

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
45
In which of the following models can interaction in an experimental design be tested?
A) a completely randomized model
B) a randomized block model
C) a two-factor model
D) all ANOVA models
A) a completely randomized model
B) a randomized block model
C) a two-factor model
D) all ANOVA models

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
46
The equation "Total SS = SSA + SSB + SS(AB) + SSE" applies to which ANOVA model?
A) one-way ANOVA
B) a two-factor factorial design
C) completely randomized design
D) randomized block design
A) one-way ANOVA
B) a two-factor factorial design
C) completely randomized design
D) randomized block design

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
47
In the two-way ANOVA, where a is the number of factor A levels, b is the number of factor B levels, and r is the number of replicates, which of the following expressions gives the formula for the number of degrees of freedom for error?
A) (a - 1)(b - 1)
B) abr - 1
C) (a - 1)(r - 1)
D) ab(r - 1)
A) (a - 1)(b - 1)
B) abr - 1
C) (a - 1)(r - 1)
D) ab(r - 1)

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
48
Given the significance level 0.05, the F-value for the degrees of freedom 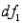 = 5 and
= 5 and 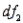 = 8 is 4.82.
= 8 is 4.82.
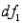 = 5 and
= 5 and 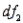 = 8 is 4.82.
= 8 is 4.82.
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
49
In the randomized block design for ANOVA, where k is the number of treatments and b is the number of blocks, how many degrees of freedom for error are there?
A) k - 1
B) b - 1
C) (k - 1)(b - 1)
D) kb - 1
A) k - 1
B) b - 1
C) (k - 1)(b - 1)
D) kb - 1

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
50
In the 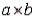 factorial experiment, where a is the number of levels for factor A, b is the number of levels for factor B, and r is the number of replications of each of the ab factor combinations, the degrees of freedom for interaction is given by which of the listed expressions below?
factorial experiment, where a is the number of levels for factor A, b is the number of levels for factor B, and r is the number of replications of each of the ab factor combinations, the degrees of freedom for interaction is given by which of the listed expressions below?
A) (a - 1)(b - 1)
B) (a - 1)(r - 1)
C) (b - 1)(r - 1)
D) ab(r - 1)
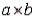 factorial experiment, where a is the number of levels for factor A, b is the number of levels for factor B, and r is the number of replications of each of the ab factor combinations, the degrees of freedom for interaction is given by which of the listed expressions below?
factorial experiment, where a is the number of levels for factor A, b is the number of levels for factor B, and r is the number of replications of each of the ab factor combinations, the degrees of freedom for interaction is given by which of the listed expressions below?A) (a - 1)(b - 1)
B) (a - 1)(r - 1)
C) (b - 1)(r - 1)
D) ab(r - 1)

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
51
A randomized block design with 4 treatments and 5 blocks produced the following sum of squares values: Total SS = 1951, SST = 349, SSE = 188. What must the value of SSB be?
A) 537
B) 1414
C) 1602
D) 1763
A) 537
B) 1414
C) 1602
D) 1763

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
52
In the randomized block design ANOVA, which of the expressions below is equal to the sum of squares for error?
A) Total SS - SST
B) Total SS - SSB
C) Total SS - SST - SSB
D) Total SS - SS(A) - SS(B) - SS(AB)
A) Total SS - SST
B) Total SS - SSB
C) Total SS - SST - SSB
D) Total SS - SS(A) - SS(B) - SS(AB)

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
53
In a two-way ANOVA, there are 4 levels for factor A, 5 levels for factor B, and 3 observations for each combination of factor A and factor B levels. What is the number of treatments in this experiment?
A) 60
B) 25
C) 20
D) 16
A) 60
B) 25
C) 20
D) 16

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
54
Three tennis players, one a beginner, one intermediate, and one advanced, have been randomly selected from the membership of a racquet facility club in a large city. Using the same tennis ball, each player hits ten serves, one with each of three racquet models, with the three racquet models selected randomly. The speed of each serve is measured with a machine and the result recorded. Among the ANOVA models listed below, which is the most likely model to fit this situation?
A) the one-way ANOVA
B) Tukey's method
C) the randomized block design
D) the matched-pairs model
A) the one-way ANOVA
B) Tukey's method
C) the randomized block design
D) the matched-pairs model

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
55
The analysis of variance (ANOVA) technique analyzes the variance of the data to determine whether differences exist between the population variances.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
56
In analysis of variances, the sum of squares for treatments (SST) is 0 when all the sample means are equal.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
57
Under which of the following conditions is a complete 3 * 2 factorial experiment said to be balanced?
A) Factor A has three levels.
B) Factor B has two levels.
C) The number of replicates is the same for each treatment.
D) The number of observations for each combination of factor A and factor B levels equal at least five.
A) Factor A has three levels.
B) Factor B has two levels.
C) The number of replicates is the same for each treatment.
D) The number of observations for each combination of factor A and factor B levels equal at least five.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
58
Analysis of variance (ANOVA) is a procedure for comparing more than two population means.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
59
In analysis of variances, the sum of squares for error (SSE) is 0 when all the sample variances are equal.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
60
What is the primary interest when designing a randomized block experiment?
A) to reduce the variation among blocks
B) to increase the between-treatments variation to more easily detect differences among the treatment means
C) to reduce the within-treatments variation to more easily detect differences among the treatment means
D) to increase the total sum of squares
A) to reduce the variation among blocks
B) to increase the between-treatments variation to more easily detect differences among the treatment means
C) to reduce the within-treatments variation to more easily detect differences among the treatment means
D) to increase the total sum of squares

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
61
In a one-way ANOVA, if the sum of squares for error (SSE) is large relative to the sum of squares for treatments (SST), this is an indication that the population means are likely to be different.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
62
In the analysis of variance, explained variation equals the mean square for treatments treatments means square in one-way ANOVA.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
63
The F statistic is the arithmetic mean of two or more means.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
64
In the analysis of variance, the sum of all samples' sums of squared deviations of individual observations from their sample mean equals the error mean square.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
65
In a one-way ANOVA, the total variation in the data across the various factor levels can be partitioned into two parts: the between-samples variation (called the sum of squares for treatments) and the within-samples variation (called the sum of squares for error).

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
66
In a one-way ANOVA, the null hypothesis is written in terms of the population variances.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
67
The one-way ANOVA requires that the sample sizes are all equal.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
68
In ANOVA, a factor is an independent variable whose values are controlled and varied by the experimenter, while a level is the intensity setting of a factor.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
69
Two-factor or two-way ANOVA is one of several versions of the analysis of variance, which controls extraneous factors by using the randomized block design.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
70
In the analysis of variance, the ANOVA table is a summary table that shows, for each source of variation, the sum of squares, the degrees of freedom, and the ratio of the sum of squares to the associated degrees of freedom (called the mean square), and also shows the F statistic.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
71
The one-way ANOVA assumes that the population means are equal.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
72
Randomization is a procedure that eliminates the effects of extraneous factors during an experiment, even prior to the administration of treatments, by creating blocks of experimental units so that all units within any one block are as alike as possible with respect to these factors.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
73
The completely randomized design is an experimental plan that creates one treatment group for each treatment, and then randomly assigns each experimental unit to one of these groups.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
74
The term "one-way ANOVA" refers to the fact that in conducting the test, there is only one way to partition the total sum of squares.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
75
Two samples of ten persons, one from the male workers and the second from the female workers of a large company, have been taken. The data involved the wage rate of each worker. To test whether there is any difference in the average wage rate between male and female workers, the most likely ANOVA design to fit this test situation is the randomized block design.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
76
One-factor or one-way ANOVA is one of several versions of the analysis of variance, which controls extraneous factors by using the randomized group design.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
77
In one-way ANOVA, there is a single factor of interest but there may be multiple levels of the factor.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
78
In a one-way ANOVA, total SS is equal to 12,345, and SST is equal to 10,685, then SSE = 1660.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
79
The equation: Total SS = SST + SSB + SSE, applies to the completely randomized design (one-way ANOVA model).

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
80
The analysis of variance, ANOVA, is best described as a statistical technique designed to test whether the means of more than two quantitative populations are equal.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck


