Chat with AI
Becker's World of the Cell 9th Edition by Lewis Kleinsmith, Jeff Hardin, Gregory Paul Bertoni
Edition 9ISBN: 9780134295510Becker's World of the Cell 9th Edition by Lewis Kleinsmith, Jeff Hardin, Gregory Paul Bertoni
Edition 9ISBN: 9780134295510 Exercise 2
Cell Sizes. To appreciate the differences in cell size illustrated in Figure 1A-1, consider these specific examples. Escherichia coli, a typical bacterial cell, is cylindrical in shape, with a diameter of about 1 µ m and a length of about 2 µ m. As a typical animal cell, consider a human liver cell, which is roughly spherical and has a diameter of about 20 µ m. For a typical plant cell, consider the columnar palisade cells located just beneath the upper surface of many plant leaves. These cells are cylindrical, with a diameter of about 20 µ m and a length of about 35 µ m.
(a)Calculate the approximate volume of each of these three cell types in cubic micrometers. (Recall that V = r 2 h for a cylinder and that V= 4 r 3 /3 for a sphere.)
(b)Approximately how many bacterial cells would fit in the internal volume of a human liver cell
(c)Approximately how many liver cells would fit inside a palisade cell
(a)Calculate the approximate volume of each of these three cell types in cubic micrometers. (Recall that V = r 2 h for a cylinder and that V= 4 r 3 /3 for a sphere.)
(b)Approximately how many bacterial cells would fit in the internal volume of a human liver cell
(c)Approximately how many liver cells would fit inside a palisade cell
Explanation
Verified
Verified
Escherichia coli has a diameter of 1 um and a length of 2 µ m.
Therefore, calculate the volume of the cell,
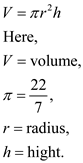Substitute the given values:
Human Liver Cells are roughly spherical, with a diameter of 20 µ m.
Therefore:
Palisade cells are cylindrical, with a diameter of 20
and a length of 35
. Therefore:
Now we have the individual volumes for each cell type, we can easily find the quantity of bacterial cells that would fit inside a human liver cell.
Hence, the number of bacterial cells that would fit in the internal volume of a human liver cell are 2,667 cells.
Now calculate the number of liver cells that would fit inside a palisade cell.
Hence, the number of liver cells that would fit in the inside a palisade cell are 2.62 cells.
Therefore, calculate the volume of the cell,
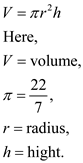Substitute the given values: Human Liver Cells are roughly spherical, with a diameter of 20 µ m. Therefore:
Palisade cells are cylindrical, with a diameter of 20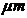 and a length of 35 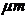. Therefore: Now we have the individual volumes for each cell type, we can easily find the quantity of bacterial cells that would fit inside a human liver cell. Hence, the number of bacterial cells that would fit in the internal volume of a human liver cell are 2,667 cells.Now calculate the number of liver cells that would fit inside a palisade cell.
Hence, the number of liver cells that would fit in the inside a palisade cell are 2.62 cells.
Becker's World of the Cell 9th Edition by Lewis Kleinsmith, Jeff Hardin, Gregory Paul Bertoni
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255
