
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540 Exercise 87
Find the least common denominator for this group of denominators using the method of prime numbers. (See Example.)
5, 18, 25, 30, 36, _____________
Finding the Least Common Denominator
Use the method of prime numbers to find the least common denominator for
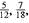 and
and
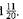
Quick TIP
It does not matter which prime number you start with; the final list of prime numbers will be the same.
SOLUTION
First write the three denominators: 12 18 20
Begin by trying to divide the three denominators by the smallest prime number, 2. Write each quotient directly above the given denominator as follows.
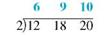
This way of writing the division is just a handy way of writing the separate problems
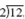 ,
,
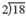 , and
, and
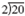 . Two of the new quotients, 6 and 10, can still be divided by 2, so perform the division again. Since 9 cannot be divided evenly by 2, just bring up the 9.
. Two of the new quotients, 6 and 10, can still be divided by 2, so perform the division again. Since 9 cannot be divided evenly by 2, just bring up the 9.

None of the new quotients in the top row can be divided by 2, so try the next prime number, 3. The numbers 3 and 9 can be divided by 3, and one of the new quotients can still be divided by 3, so the division is performed again.

Since none of the new quotients in the top row can be divided by 3, try the next prime number, 5. The number 5 can be used only once, as shown.
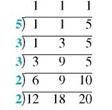
Now that the top row contains only 1s, find the least common denominator by multiplying the prime numbers in the left column: 2 × 2 × 3 × 3 × 5 = 180.
5, 18, 25, 30, 36, _____________
Finding the Least Common Denominator
Use the method of prime numbers to find the least common denominator for
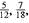 and
and 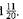
Quick TIP
It does not matter which prime number you start with; the final list of prime numbers will be the same.
SOLUTION
First write the three denominators: 12 18 20
Begin by trying to divide the three denominators by the smallest prime number, 2. Write each quotient directly above the given denominator as follows.
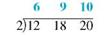
This way of writing the division is just a handy way of writing the separate problems
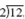 ,
, 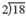 , and
, and 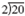 . Two of the new quotients, 6 and 10, can still be divided by 2, so perform the division again. Since 9 cannot be divided evenly by 2, just bring up the 9.
. Two of the new quotients, 6 and 10, can still be divided by 2, so perform the division again. Since 9 cannot be divided evenly by 2, just bring up the 9.
None of the new quotients in the top row can be divided by 2, so try the next prime number, 3. The numbers 3 and 9 can be divided by 3, and one of the new quotients can still be divided by 3, so the division is performed again.

Since none of the new quotients in the top row can be divided by 3, try the next prime number, 5. The number 5 can be used only once, as shown.

Now that the top row contains only 1s, find the least common denominator by multiplying the prime numbers in the left column: 2 × 2 × 3 × 3 × 5 = 180.
Explanation
To find the lowest common denominator fo...
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


