
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540 Exercise 121
Prime numbers are used to find the least common denominator. Write the definition of a prime number in your own words. (See Objective.)
Find the least common denominator. Fractions with different denominators, such as
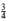 and
and
 , are unlike fractions. Add or subtract unlike fractions by first writing the fractions with a common denominator. The least common denominator (LCD) for two or more fractions is the smallest whole number that can be divided, without a remainder, by all the denominators of the fractions. For example, the LCD of the fractions
, are unlike fractions. Add or subtract unlike fractions by first writing the fractions with a common denominator. The least common denominator (LCD) for two or more fractions is the smallest whole number that can be divided, without a remainder, by all the denominators of the fractions. For example, the LCD of the fractions
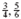 , and
, and
 is 12, since 12 is the smallest number that can be divided evenly by 4, 6, and 2.
is 12, since 12 is the smallest number that can be divided evenly by 4, 6, and 2.
There are two methods of finding the least common denominator:
Inspection. With small denominators, it may be possible to find the least common denominator by inspection. For example, the LCD for
 and
and
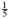 is 15, the smallest number that can be divided evenly by both 3 and 5.
is 15, the smallest number that can be divided evenly by both 3 and 5.
Method of prime numbers. If the LCD cannot be found by inspection, use the method of prime numbers, as shown in the next two examples. First, we define a prime number.

Find the least common denominator. Fractions with different denominators, such as
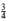 and
and  , are unlike fractions. Add or subtract unlike fractions by first writing the fractions with a common denominator. The least common denominator (LCD) for two or more fractions is the smallest whole number that can be divided, without a remainder, by all the denominators of the fractions. For example, the LCD of the fractions
, are unlike fractions. Add or subtract unlike fractions by first writing the fractions with a common denominator. The least common denominator (LCD) for two or more fractions is the smallest whole number that can be divided, without a remainder, by all the denominators of the fractions. For example, the LCD of the fractions 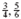 , and
, and  is 12, since 12 is the smallest number that can be divided evenly by 4, 6, and 2.
is 12, since 12 is the smallest number that can be divided evenly by 4, 6, and 2.There are two methods of finding the least common denominator:
Inspection. With small denominators, it may be possible to find the least common denominator by inspection. For example, the LCD for
 and
and 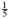 is 15, the smallest number that can be divided evenly by both 3 and 5.
is 15, the smallest number that can be divided evenly by both 3 and 5.Method of prime numbers. If the LCD cannot be found by inspection, use the method of prime numbers, as shown in the next two examples. First, we define a prime number.

Explanation
Prime numbers are those number...
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


