
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540 Exercise 42
Subtract. Write each answer in lowest terms. (See Example.)
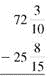
Subtracting with Borrowing
(a) Subtract
 from
from
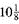 .
.
(b) Subtract
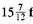 rom 41.
rom 41.
Quick TIP
You do not have to write fractions using the least common denominator when adding or subtracting on a calculator.
SOLUTION
Start by rewriting each problem with a common denominator.
(a)

Subtracting
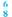 from
from
 requires borrowing from the whole number 10.
requires borrowing from the whole number 10.
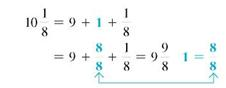
Rewrite the problem as shown. Check by adding
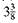 and
and
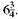 The answer should be
The answer should be
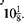
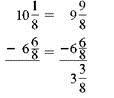
(b)
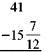
To subtract the fraction
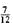 requires borrowing 1 whole unit from 41.
requires borrowing 1 whole unit from 41.
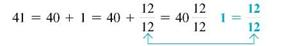
Rewrite the problem as shown. Check by adding
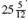 and
and
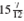 . The answer should be 41.
. The answer should be 41.
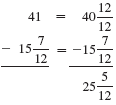
The calculator solution to part (a) uses the fraction key.

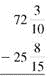
Subtracting with Borrowing
(a) Subtract
 from
from 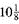 .
.(b) Subtract
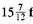 rom 41.
rom 41.Quick TIP
You do not have to write fractions using the least common denominator when adding or subtracting on a calculator.
SOLUTION
Start by rewriting each problem with a common denominator.
(a)

Subtracting
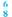 from
from  requires borrowing from the whole number 10.
requires borrowing from the whole number 10.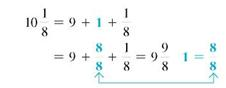
Rewrite the problem as shown. Check by adding
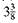 and
and 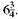 The answer should be
The answer should be 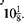
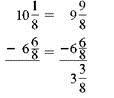
(b)
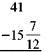
To subtract the fraction
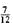 requires borrowing 1 whole unit from 41.
requires borrowing 1 whole unit from 41.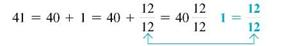
Rewrite the problem as shown. Check by adding
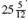 and
and 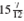 . The answer should be 41.
. The answer should be 41.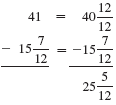
The calculator solution to part (a) uses the fraction key.

Explanation
To subtract from
first determine wheth...
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


