
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540 Exercise 51
Solve the following application problem. Read problem carefully to decide which are increase or decrease problem, and work accordingly. (See Examples.)
Using a Diagram to Understand an Increase Problem
The value of a home sold by Tom Dugally this year is $203,500, which is 10, more than last year's value. Find the value of the home last year.
SOLUTION
CASE IN POINT The phrase "10% more than last year's value," tells us that last year's value is the base and that it is the unknown. The figure below shows last year's value as 100% and this year's value which is:
(the base + 10% more than last year's value) = 110% of the base
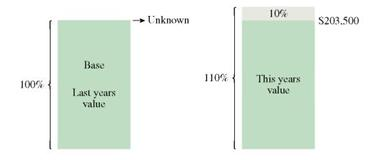
The diagram shows that the 10, increase is based on last year's value which is not known. It is not based on this year's value of $203,500. This year's value is last year's value plus 10, of last year's value.
Use the basic percent formula to solve for base in increase problems.

Substituting in the percent formula with part = $203,500 and rate = 110, results in the following.
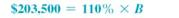
Quick TIP
The common error in solving an increase problem is thinking that the base is given and that the solution can be found by solving for part.
Solving for B results in the following equation, which is solved for B.
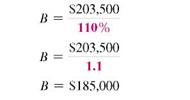
So the value of the house last year was $185,000. Now check the answer.

$203,500 is 110, of $185,000.
Finding Base after Two Increases
Due to increased demand for a patented process that will help analyze the DNA of mice, Biotics Genome has increased production of testing kits by 20, per year for each of the two past years. This year's production is 93,600 kits. Find the number of kits produced two years ago.
SOLUTION
The two 20, increases cannot be added together since the two increases act on different bases. Solve this problem in two steps, one for each of the 20, increases. First, use a diagram to find last year's production of DNA kits.
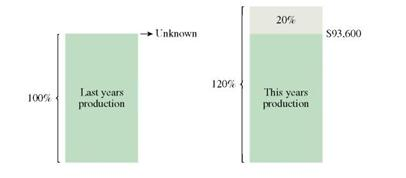
Last year's production plus 20% of last year's production equals this year's production. So, part ( P ) = 93,600 and rate ( R ) = 120%
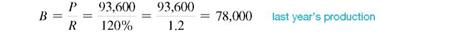
The number of DNA testing kits produced last year was 78,000. Use this number and knowledge that the sales volume increased 20, from 2 years ago to last year to find production 2 years ago.
Quick TIP
It is important to realize that the two 20, increases cannot be added together to equal one increase of 40,. Each 20, increase is calculated on a different base.
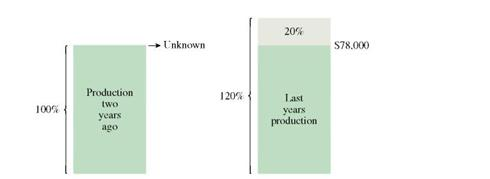
Production two years ago added to 20, of that production equals last year's production. So, part ( P ) = 78,000 and rate ( R ) = 120% once again.
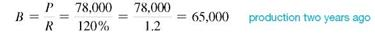
The calculator solution to this example is done by dividing in a series.

Check the answer.

Using a Diagram to Understand a Decrease Problem
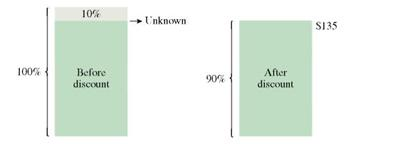
After Nike deducted 10, from the price of a pair of competition running shoes, Katie Small paid $135. What was the original price of the shoes?
SOLUTION
The phrase "deducted 10, from the price" indicates it is a decrease problem. The original price is the unknown.
Quick TIP
The common error made in decrease problems is thinking that the reduced price is the base. The original price is actually the base.
Ten percent was deducted from the original price. The resulting price paid of $135 is 90, of the original price. So, part ( P ) = $135 and rate ( R ) = 90%
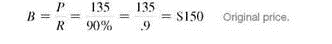
Check the answer.

COLLEGE EXPENSES After spending $3450 for tuition and $4350 for dormitory fees, Edgar Espina finds that 35, of his original savings remains. Find the amount of his savings that remains. ________________
Using a Diagram to Understand an Increase Problem
The value of a home sold by Tom Dugally this year is $203,500, which is 10, more than last year's value. Find the value of the home last year.
SOLUTION
CASE IN POINT The phrase "10% more than last year's value," tells us that last year's value is the base and that it is the unknown. The figure below shows last year's value as 100% and this year's value which is:
(the base + 10% more than last year's value) = 110% of the base

The diagram shows that the 10, increase is based on last year's value which is not known. It is not based on this year's value of $203,500. This year's value is last year's value plus 10, of last year's value.
Use the basic percent formula to solve for base in increase problems.

Substituting in the percent formula with part = $203,500 and rate = 110, results in the following.
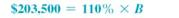
Quick TIP
The common error in solving an increase problem is thinking that the base is given and that the solution can be found by solving for part.
Solving for B results in the following equation, which is solved for B.
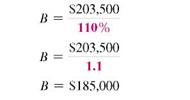
So the value of the house last year was $185,000. Now check the answer.

$203,500 is 110, of $185,000.
Finding Base after Two Increases

Due to increased demand for a patented process that will help analyze the DNA of mice, Biotics Genome has increased production of testing kits by 20, per year for each of the two past years. This year's production is 93,600 kits. Find the number of kits produced two years ago.
SOLUTION
The two 20, increases cannot be added together since the two increases act on different bases. Solve this problem in two steps, one for each of the 20, increases. First, use a diagram to find last year's production of DNA kits.

Last year's production plus 20% of last year's production equals this year's production. So, part ( P ) = 93,600 and rate ( R ) = 120%
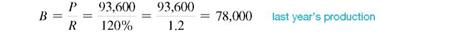
The number of DNA testing kits produced last year was 78,000. Use this number and knowledge that the sales volume increased 20, from 2 years ago to last year to find production 2 years ago.
Quick TIP
It is important to realize that the two 20, increases cannot be added together to equal one increase of 40,. Each 20, increase is calculated on a different base.

Production two years ago added to 20, of that production equals last year's production. So, part ( P ) = 78,000 and rate ( R ) = 120% once again.
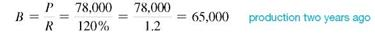
The calculator solution to this example is done by dividing in a series.

Check the answer.

Using a Diagram to Understand a Decrease Problem
After Nike deducted 10, from the price of a pair of competition running shoes, Katie Small paid $135. What was the original price of the shoes?
SOLUTION
The phrase "deducted 10, from the price" indicates it is a decrease problem. The original price is the unknown.

Quick TIP
The common error made in decrease problems is thinking that the reduced price is the base. The original price is actually the base.
Ten percent was deducted from the original price. The resulting price paid of $135 is 90, of the original price. So, part ( P ) = $135 and rate ( R ) = 90%
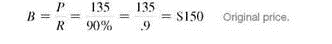
Check the answer.

COLLEGE EXPENSES After spending $3450 for tuition and $4350 for dormitory fees, Edgar Espina finds that 35, of his original savings remains. Find the amount of his savings that remains. ________________
Explanation
Set the total spending of tuition and do...
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


