
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540 Exercise 25
Find the missing numbers. Round rates to the nearest tenth of a percent and dollar amounts to the nearest cent. (See Examples.)
 Using the Basic Markup Formula
Using the Basic Markup Formula

REI received three different types of snowshoes in one shipment. Use the basic markup formula to find the unknown for each of the following.
(a)
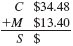
(b)
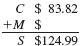
(c)
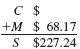
SOLUTION
CASE IN POINT
(a)
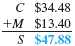
(b)
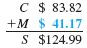
(c)
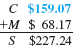
Solving for Percent of Markup on Cost

The manager of a discount store bought hiking boots manufactured in Mexico for $60 and plans to sell them for $81 a pair. Find the percent of markup based on cost.
SOLUTION
Set up the problem using the table form given earlier. Since this problem is related to markup based on cost, cost is the base, or 100%. All other percents must be in terms of cost.
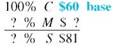
Find the unknown values as follows.
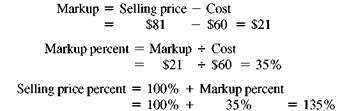
The following table shows that the markup based on cost is 35% and that the selling price is 135% of cost.
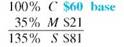
The calculator solution to the first part of this example is as follows.
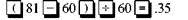
Note: Refer to Appendix B for calculator basics.
Finding Cost When Cost Is Base

Olympic Sports places a markup on a 50-lb iron barbell set of $16, which is 50, based on cost. Find the cost and the selling price.
Quick TIP
It is important to first find the base (the cost in this problem) and then find the other values in the table.
SOLUTION
Set up the table using the fact that the markup of 50, based on cost is $16. Cost is the base, or 100%. Cost is not known.
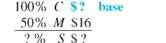
Find the cost using the fact that markup of $16 is 50% of cost.
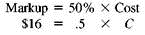
Divide both sides of the equation by.5 to find

Complete the table by adding the percent and dollar columns to find the totals.
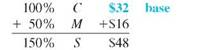
The weight set costs the retailer $32 and is marked up by $16. The selling price of $48 is 150% of the cost of $32.
Finding the Markup and the Selling Price

Find the markup and the selling price for an Adidas hooded sweatshirt if the cost is $23.60 and the markup is 45% of cost.
SOLUTION
Use the information given to set up the problem.
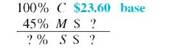
The percent column totals to 145%. Use the basic percent equation to find the following.
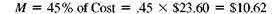
The selling price can be found either by adding the cost of $23.60 to the markup of $10.62, or as follows:
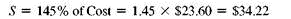
The table shows that the selling price of the hooded sweatshirt is $34.22.
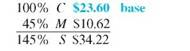
This calculator solution uses the percent add-on feature found on many calculators.
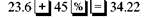
Finding Cost When Cost Is Base
REI sells a lightweight down sleeping bag rated for very cold weather for $308. If the markup on cost is 40%, find the amount that REI pays for one sleeping bag. Then find the markup.

SOLUTION
CASE IN POINT The cost is 100% and the markup is 40%, so the selling price is 140% of cost.
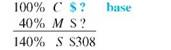
: is important to notice that the base is not known in this example. So, use the basic percent quation to find the base or think through it as follows:
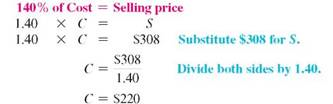
So, the sleeping bag cost $220. Finally, markup = selling price ? cost.
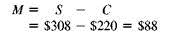
All values are given in the table.
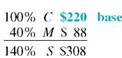
Check the answer by making sure that both column totals are correct.
Finding the Cost and the Markup
The retail price of a 50-inch portable basketball system is $549.99. The retailer has operating expenses of 29.5% and wants a 5.5% profit, both based on cost, on this item. First find the total percent of markup on cost; then find cost and markup.
Quick TIP
Remember, when calculating markup on cost, cost is always the base and 100% always goes next to cost.
SOLUTION
Add operating expense and profit percents to find the percent markup on cost required by the retailer.
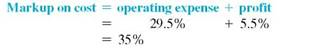
Now set the problem up in the table form.

The final table is shown.
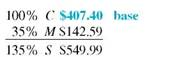
The cost is $407.40 and the markup is $142.59.
 Using the Basic Markup Formula
Using the Basic Markup Formula 
REI received three different types of snowshoes in one shipment. Use the basic markup formula to find the unknown for each of the following.
(a)
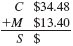
(b)
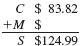
(c)
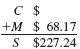
SOLUTION
CASE IN POINT
(a)
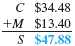
(b)
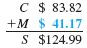
(c)
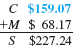
Solving for Percent of Markup on Cost

The manager of a discount store bought hiking boots manufactured in Mexico for $60 and plans to sell them for $81 a pair. Find the percent of markup based on cost.
SOLUTION
Set up the problem using the table form given earlier. Since this problem is related to markup based on cost, cost is the base, or 100%. All other percents must be in terms of cost.
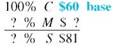
Find the unknown values as follows.
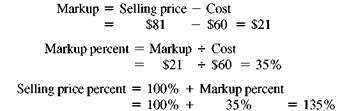
The following table shows that the markup based on cost is 35% and that the selling price is 135% of cost.
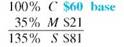
The calculator solution to the first part of this example is as follows.
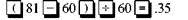
Note: Refer to Appendix B for calculator basics.
Finding Cost When Cost Is Base

Olympic Sports places a markup on a 50-lb iron barbell set of $16, which is 50, based on cost. Find the cost and the selling price.
Quick TIP
It is important to first find the base (the cost in this problem) and then find the other values in the table.
SOLUTION
Set up the table using the fact that the markup of 50, based on cost is $16. Cost is the base, or 100%. Cost is not known.
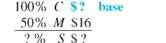
Find the cost using the fact that markup of $16 is 50% of cost.
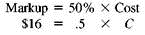
Divide both sides of the equation by.5 to find

Complete the table by adding the percent and dollar columns to find the totals.
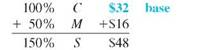
The weight set costs the retailer $32 and is marked up by $16. The selling price of $48 is 150% of the cost of $32.
Finding the Markup and the Selling Price

Find the markup and the selling price for an Adidas hooded sweatshirt if the cost is $23.60 and the markup is 45% of cost.
SOLUTION
Use the information given to set up the problem.
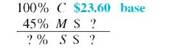
The percent column totals to 145%. Use the basic percent equation to find the following.
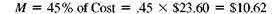
The selling price can be found either by adding the cost of $23.60 to the markup of $10.62, or as follows:
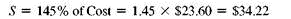
The table shows that the selling price of the hooded sweatshirt is $34.22.
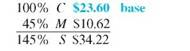
This calculator solution uses the percent add-on feature found on many calculators.
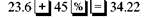
Finding Cost When Cost Is Base
REI sells a lightweight down sleeping bag rated for very cold weather for $308. If the markup on cost is 40%, find the amount that REI pays for one sleeping bag. Then find the markup.

SOLUTION
CASE IN POINT The cost is 100% and the markup is 40%, so the selling price is 140% of cost.
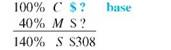
: is important to notice that the base is not known in this example. So, use the basic percent quation to find the base or think through it as follows:

So, the sleeping bag cost $220. Finally, markup = selling price ? cost.
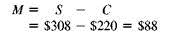
All values are given in the table.
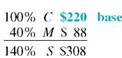
Check the answer by making sure that both column totals are correct.
Finding the Cost and the Markup
The retail price of a 50-inch portable basketball system is $549.99. The retailer has operating expenses of 29.5% and wants a 5.5% profit, both based on cost, on this item. First find the total percent of markup on cost; then find cost and markup.
Quick TIP
Remember, when calculating markup on cost, cost is always the base and 100% always goes next to cost.
SOLUTION
Add operating expense and profit percents to find the percent markup on cost required by the retailer.
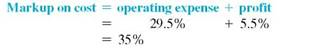
Now set the problem up in the table form.

The final table is shown.
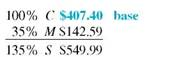
The cost is $407.40 and the markup is $142.59.
Explanation
In this problem, we are given the cost p...
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


