
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540 Exercise 68
Use values from the compound interest table on page to find both the compound amount and the compound interest. Round the compound amount to the nearest cent. (See Examples.)
Finding the Interest Rate per Compounding Period and the
Number of Compounding Periods
Find the interest rate per compounding period and the number of compounding periods for each.
(a) 5% compounded semiannually, 3 years
(b) 6% per year, compounded monthly,
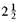 years
years
(c) 2% per year, compounded quarterly, 5 years
SOLUTION
(a) 5% compounded semiannually is
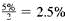 credited at the end of each 6 months. There are 3 years ×2 periods per year = 6 compounding periods in 3 years.
credited at the end of each 6 months. There are 3 years ×2 periods per year = 6 compounding periods in 3 years.
(b) 6% per year, compounded monthly, results in
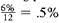 credited at the end of each month. There are 2.5 years ×12 periods per year = 30 compounding periods in 2.5 years.
credited at the end of each month. There are 2.5 years ×12 periods per year = 30 compounding periods in 2.5 years.
(c) 2% per year, compounded quarterly, results in
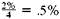 credited at the end of each quarter. There are 5 years ×4 periods per year = 20 compounding periods in 5 years.
credited at the end of each quarter. There are 5 years ×4 periods per year = 20 compounding periods in 5 years.
Finding Compound Interest
An investment managed by Bank of America pays 7, interest per year compounded semian-nually. Given an initial deposit of $4500, (a) use the formula to find the compound amount after 5 years, and (b) find the compound interest.
SOLUTION
(a) Interest is compounded at
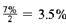 every 6 months for 5 years × 2 periods per year = 10 periods. Therefore, 3.5% is the interest rate per compounding period ( i ) and 10 is the number of compounding periods ( n ).
every 6 months for 5 years × 2 periods per year = 10 periods. Therefore, 3.5% is the interest rate per compounding period ( i ) and 10 is the number of compounding periods ( n ).
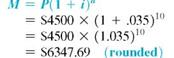
The compound amount is $6347.69.
(b)
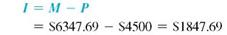
The interest is $1847.69.
The calculator solution for part (a) is as follows.
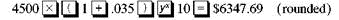
Note: Refer to Appendix B for calculator basics.
Finding Compound Interest
In each case, find the interest earned on a $2000 deposit.
(a) For 3 years, compounded annually at 4%
(b) For 5 years, compounded semiannually at 6%
(c) For 6 years, compounded quarterly at 8%
(d) For 2 years, compounded monthly at 12%
SOLUTION
(a) In 3 years, there are 3 × 1 = 3 compounding periods. The interest rate per compounding period is 4%, 1 = 4%. Look across the top of the compound interest table above for 4% and down the side for 3 periods to find 1.12486.
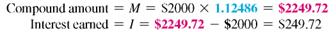
(b) In 5 years, there are 5 × 2 = 10 semiannual compounding periods. The interest rate per compounding period is 6% ÷ 2 = 3%. In the compound interest table, look at 3% at the top and 10 periods down the side to find 1.34392.
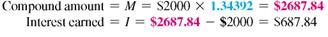
(c) Interest compounded quarterly is compounded 4 times a year. In 6 years, there are
6 × 4 = 24 quarters, or 24 periods. Interest of 8% per year is
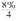 = 2% per quarter. In the compound interest table, locate 2% across the top and 24 periods at the left, finding the number 1.60844.
= 2% per quarter. In the compound interest table, locate 2% across the top and 24 periods at the left, finding the number 1.60844.
(d) In 2 years, there are 2 × 12 = 24 monthly periods. Interest of 12% per year is
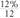 = 1% per month. Look in the compound interest table for 1% and 24 periods, finding the number 1.26973.
= 1% per month. Look in the compound interest table for 1% and 24 periods, finding the number 1.26973.
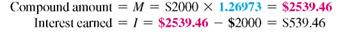
Finding Compound Interest
John Smith sold his truck for $15,000, which he deposited in a retirement account that pays interest compounded semiannually. How much will he have after 15 years if the funds grow at
(a) 6%?
(b) 8%?
(c) 10%?
SOLUTION
In 15 years, there are 15 × 2 = 30 semiannual periods. The semiannual interest rates are


Finding the Interest Rate per Compounding Period and the
Number of Compounding Periods
Find the interest rate per compounding period and the number of compounding periods for each.
(a) 5% compounded semiannually, 3 years
(b) 6% per year, compounded monthly,
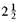 years
years(c) 2% per year, compounded quarterly, 5 years
SOLUTION
(a) 5% compounded semiannually is
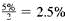 credited at the end of each 6 months. There are 3 years ×2 periods per year = 6 compounding periods in 3 years.
credited at the end of each 6 months. There are 3 years ×2 periods per year = 6 compounding periods in 3 years.(b) 6% per year, compounded monthly, results in
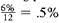 credited at the end of each month. There are 2.5 years ×12 periods per year = 30 compounding periods in 2.5 years.
credited at the end of each month. There are 2.5 years ×12 periods per year = 30 compounding periods in 2.5 years.(c) 2% per year, compounded quarterly, results in
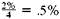 credited at the end of each quarter. There are 5 years ×4 periods per year = 20 compounding periods in 5 years.
credited at the end of each quarter. There are 5 years ×4 periods per year = 20 compounding periods in 5 years.Finding Compound Interest
An investment managed by Bank of America pays 7, interest per year compounded semian-nually. Given an initial deposit of $4500, (a) use the formula to find the compound amount after 5 years, and (b) find the compound interest.
SOLUTION
(a) Interest is compounded at
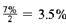 every 6 months for 5 years × 2 periods per year = 10 periods. Therefore, 3.5% is the interest rate per compounding period ( i ) and 10 is the number of compounding periods ( n ).
every 6 months for 5 years × 2 periods per year = 10 periods. Therefore, 3.5% is the interest rate per compounding period ( i ) and 10 is the number of compounding periods ( n ).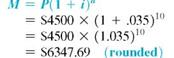
The compound amount is $6347.69.
(b)
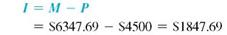
The interest is $1847.69.
The calculator solution for part (a) is as follows.
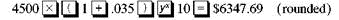
Note: Refer to Appendix B for calculator basics.
Finding Compound Interest
In each case, find the interest earned on a $2000 deposit.
(a) For 3 years, compounded annually at 4%
(b) For 5 years, compounded semiannually at 6%
(c) For 6 years, compounded quarterly at 8%
(d) For 2 years, compounded monthly at 12%
SOLUTION
(a) In 3 years, there are 3 × 1 = 3 compounding periods. The interest rate per compounding period is 4%, 1 = 4%. Look across the top of the compound interest table above for 4% and down the side for 3 periods to find 1.12486.
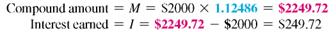
(b) In 5 years, there are 5 × 2 = 10 semiannual compounding periods. The interest rate per compounding period is 6% ÷ 2 = 3%. In the compound interest table, look at 3% at the top and 10 periods down the side to find 1.34392.
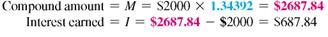
(c) Interest compounded quarterly is compounded 4 times a year. In 6 years, there are
6 × 4 = 24 quarters, or 24 periods. Interest of 8% per year is
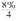 = 2% per quarter. In the compound interest table, locate 2% across the top and 24 periods at the left, finding the number 1.60844.
= 2% per quarter. In the compound interest table, locate 2% across the top and 24 periods at the left, finding the number 1.60844.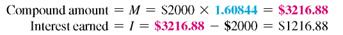
(d) In 2 years, there are 2 × 12 = 24 monthly periods. Interest of 12% per year is
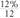 = 1% per month. Look in the compound interest table for 1% and 24 periods, finding the number 1.26973.
= 1% per month. Look in the compound interest table for 1% and 24 periods, finding the number 1.26973.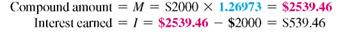
Finding Compound Interest
John Smith sold his truck for $15,000, which he deposited in a retirement account that pays interest compounded semiannually. How much will he have after 15 years if the funds grow at
(a) 6%?
(b) 8%?
(c) 10%?
SOLUTION
In 15 years, there are 15 × 2 = 30 semiannual periods. The semiannual interest rates are


Explanation
The following table is given, There are...
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


