
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540 Exercise 48
Find the present value of the following. Round to the nearest cent. Also, find the amount of interest earned. (See Examples.)
Finding Present Value

Betty Clark needs to replace two pumps at her gas station in 3 years at an estimated cost of $12,000. What lump sum deposited today at 5% compounded annually must she invest to have the needed funds? How much interest will she earn?
SOLUTION
Step 1 The interest rate is 5% per compounding period for 3 compounding periods (years in this case). Look across the top of the table for 5% and down the left column for 3 to find.86384.
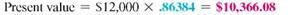
Step 2 Interest earned = $12,000 ? $10,366.08 = $1633.92.
Step 3 Check the answer by finding the future value of an investment of $10,366.08 in an account earning 5% compounded annually for 3 years. Use the table on page to find 1.15763.

The reason it is not exactly $12,000 is rounding in the table value.
Finding Present Value

The local Harley-Davidson shop has seen business grow rapidly. The owners plan to increase the size of their 6000-square-foot shop in one year at a cost of $280,000. How much should be invested in an investment earning 6, compounded semiannually to have the funds needed?
SOLUTION
The interest rate per compounding period is
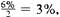 and the number of compounding periods is 1 year × 2 periods per year = 2. Use the table to find.94260.
and the number of compounding periods is 1 year × 2 periods per year = 2. Use the table to find.94260.
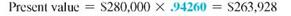
The difference between the $280,001.22 and the desired $280,000 is due to rounding.
SELF-EMPLOYMENT Janet Becker wishes to start her own day-care business in her home in 4 years and estimates that she will need $25,000 to do so. (a) What lump sum should be invested today at 5%, compounded semi-annually, to produce the needed amount? __________________ (b) How much interest will be earned? __________________

Finding Present Value

Betty Clark needs to replace two pumps at her gas station in 3 years at an estimated cost of $12,000. What lump sum deposited today at 5% compounded annually must she invest to have the needed funds? How much interest will she earn?
SOLUTION
Step 1 The interest rate is 5% per compounding period for 3 compounding periods (years in this case). Look across the top of the table for 5% and down the left column for 3 to find.86384.
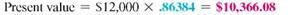
Step 2 Interest earned = $12,000 ? $10,366.08 = $1633.92.
Step 3 Check the answer by finding the future value of an investment of $10,366.08 in an account earning 5% compounded annually for 3 years. Use the table on page to find 1.15763.

The reason it is not exactly $12,000 is rounding in the table value.
Finding Present Value

The local Harley-Davidson shop has seen business grow rapidly. The owners plan to increase the size of their 6000-square-foot shop in one year at a cost of $280,000. How much should be invested in an investment earning 6, compounded semiannually to have the funds needed?
SOLUTION
The interest rate per compounding period is
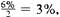 and the number of compounding periods is 1 year × 2 periods per year = 2. Use the table to find.94260.
and the number of compounding periods is 1 year × 2 periods per year = 2. Use the table to find.94260.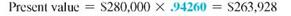
The difference between the $280,001.22 and the desired $280,000 is due to rounding.
SELF-EMPLOYMENT Janet Becker wishes to start her own day-care business in her home in 4 years and estimates that she will need $25,000 to do so. (a) What lump sum should be invested today at 5%, compounded semi-annually, to produce the needed amount? __________________ (b) How much interest will be earned? __________________

Explanation
The following table is given,
The inte...
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


