
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Edition 12ISBN: 978-0132605540 Exercise 47
Find the amount of this ordinary annuities rounded to the nearest cent. Find the total interest earned. (See Examples.)
Finding the Value of an Annuity and Interest Earned
Roman Rodriguez's employer will match his contributions into a retirement plan up to 5% of his $32,000 annual salary. In other words, the employer will put $1 into his retirement plan for every $1 Rodriguez puts into his retirement plan up to the limit. Find the future amount in 8 years if every quarter he contributes the maximum allowed assuming (a) funds earn 4% compounded quarterly and (b) funds earn 8% compounded quarterly. (c) Then find the difference between the two.
CASE IN POINT
SOLUTION
Salary per quater = $32,000 ÷ 4 = $8000
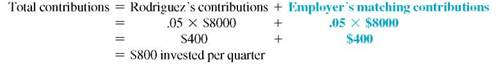
(a) Interest of
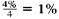 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
Amount = $800 × 37.49407 = $29,995.26 (rounded)
(b) Interest of
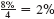 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
Amount = $800 × 44.22703 = $35,381.62 (rounded)
(c) Difference = $35,381.62 ? $30,295.21 = $5086.41
Finding the Amount of an Annuity and Interest Earned

At the birth of her grandson, Junella Smith commits to help pay for his college education. She decides to make deposits of $600 at the end of each 6 months into an account for 17 years. Find the amount of the annuity and the interest earned, assuming 6% compounded semiannually.
SOLUTION
Interest of
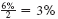 is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
Amount = $600 × 57.73018 = $ 34,638.11
Interest = $34,638.11 ? ( 34 × $600) = $14,238.11 (rounded)
Smith knows that a college education will cost a lot more in 17 years than it does now, but she also knows that $34,638.11 will be of great help to her grandson.
Financial Calculator solution
In this example, payment ($600), interest rate per compounding period (3,), and number of compounding periods (34) are known. Future value is the unknown. Enter the payment as a negative number since it is an outflow of cash that Junella Smith pays each month. Finally, press the
 key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.

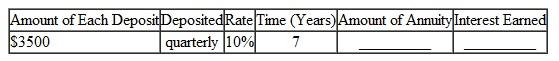
Finding the Value of an Annuity and Interest Earned
Roman Rodriguez's employer will match his contributions into a retirement plan up to 5% of his $32,000 annual salary. In other words, the employer will put $1 into his retirement plan for every $1 Rodriguez puts into his retirement plan up to the limit. Find the future amount in 8 years if every quarter he contributes the maximum allowed assuming (a) funds earn 4% compounded quarterly and (b) funds earn 8% compounded quarterly. (c) Then find the difference between the two.
CASE IN POINT
SOLUTION
Salary per quater = $32,000 ÷ 4 = $8000
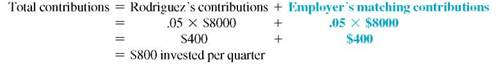
(a) Interest of
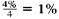 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407. Amount = $800 × 37.49407 = $29,995.26 (rounded)
(b) Interest of
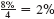 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703. Amount = $800 × 44.22703 = $35,381.62 (rounded)
(c) Difference = $35,381.62 ? $30,295.21 = $5086.41
Finding the Amount of an Annuity and Interest Earned

At the birth of her grandson, Junella Smith commits to help pay for his college education. She decides to make deposits of $600 at the end of each 6 months into an account for 17 years. Find the amount of the annuity and the interest earned, assuming 6% compounded semiannually.
SOLUTION
Interest of
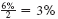 is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.Amount = $600 × 57.73018 = $ 34,638.11
Interest = $34,638.11 ? ( 34 × $600) = $14,238.11 (rounded)
Smith knows that a college education will cost a lot more in 17 years than it does now, but she also knows that $34,638.11 will be of great help to her grandson.
Financial Calculator solution
In this example, payment ($600), interest rate per compounding period (3,), and number of compounding periods (34) are known. Future value is the unknown. Enter the payment as a negative number since it is an outflow of cash that Junella Smith pays each month. Finally, press the
 key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
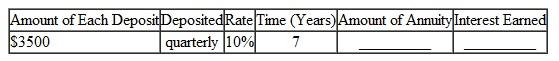
Explanation
The following table is given, There are...
Business Mathematics Brief 12th Edition by Stanley Salzman ,Gary Clendenen, Charles Miller
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


