
Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase
Edition 6ISBN: 978-1111827021
Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase
Edition 6ISBN: 978-1111827021 Exercise 30
Draw a scatter diagram displaying the data.
(b) Verify the given sums x , y , x 2 , y 2 , and xy , and the value of the sample correlation coefficient r.
(c) Find
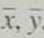 , a , and b. Then find the equation of the least-squares line = a + bx.
, a , and b. Then find the equation of the least-squares line = a + bx.
(d) Graph the least-squares line on your scatter diagram. Be sure to use the point(
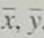 ) as one of the points on the line.
) as one of the points on the line.
(e) Interpretation Find the value of the coefficient of determination r 2. What percentage of the variation in y can be explained by the corresponding variation in x and the least-squares line What percentage is unexplained Answers may vary slightly due to rounding.
Research: Patents The following data are based on information from the Harvard Business Review (Vol. 72, No. 1). Let x be the number of different research programs, and let y be the mean number of patents per program. As in any business, a company can spread itself too thin. For example, too many research programs might lead to a decline in overall research productivity. The following data are for a collection of pharmaceutical companies and their research programs:

Complete parts (a) through (e), given x = 90, y = 8.1, x ² = 1420, y ² = 11.83, xy = 113.8, and r -0.973.
(f) Suppose a pharmaceutical company has 15 different research programs. What does the least-squares equation forecast for y = mean number of patents per program
(b) Verify the given sums x , y , x 2 , y 2 , and xy , and the value of the sample correlation coefficient r.
(c) Find
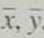 , a , and b. Then find the equation of the least-squares line = a + bx.
, a , and b. Then find the equation of the least-squares line = a + bx.(d) Graph the least-squares line on your scatter diagram. Be sure to use the point(
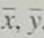 ) as one of the points on the line.
) as one of the points on the line.(e) Interpretation Find the value of the coefficient of determination r 2. What percentage of the variation in y can be explained by the corresponding variation in x and the least-squares line What percentage is unexplained Answers may vary slightly due to rounding.
Research: Patents The following data are based on information from the Harvard Business Review (Vol. 72, No. 1). Let x be the number of different research programs, and let y be the mean number of patents per program. As in any business, a company can spread itself too thin. For example, too many research programs might lead to a decline in overall research productivity. The following data are for a collection of pharmaceutical companies and their research programs:

Complete parts (a) through (e), given x = 90, y = 8.1, x ² = 1420, y ² = 11.83, xy = 113.8, and r -0.973.
(f) Suppose a pharmaceutical company has 15 different research programs. What does the least-squares equation forecast for y = mean number of patents per program
Explanation
We are studying the linear relationship ...
Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


