
Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase
Edition 6ISBN: 978-1111827021
Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase
Edition 6ISBN: 978-1111827021 Exercise 69
Expand Your Knowledge: Alternate Method for Confidence Intervals When is unknown and the sample is of size n 30, there are two methods for computing confidence intervals for .
Method 1: Use the Student's t distribution with d.f. = n - 1.
This is the method used in the text. It is widely employed in statistical studies. Also, most statistical software packages use this method.
Method 2: When n 30, use the sample standard deviation s as an estimate for , and then use the standard normal distribution.
This method is based on the fact that for large samples, s is a fairly good approximation for . Also, for large n, the critical values for the Student's t distribution approach those of the standard normal distribution.
Consider a random sample of size n = 31, with sample mean
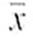 = 45.2 and sample standard deviation s = 5.3.
= 45.2 and sample standard deviation s = 5.3.
(a) Compute 90%, 95%, and 99% confidence intervals for using Method 1 with a Student's t distribution. Round endpoints to two digits after the decimal.
(b) Compute 90%, 95%, and 99% confidence intervals for using Method 2 with the standard normal distribution. Use s as an estimate for . Round endpoints to two digits after the decimal.
(c) Compare intervals for the two methods. Would you say that confidence intervals using a Student's t distribution are more conservative in the sense that they tend to be longer than intervals based on the standard normal distribution
(d) Repeat parts (a) through (c) for a sample of size n = 81. With increased sample size, do the two methods give respective confidence intervals that are more similar
Method 1: Use the Student's t distribution with d.f. = n - 1.
This is the method used in the text. It is widely employed in statistical studies. Also, most statistical software packages use this method.
Method 2: When n 30, use the sample standard deviation s as an estimate for , and then use the standard normal distribution.
This method is based on the fact that for large samples, s is a fairly good approximation for . Also, for large n, the critical values for the Student's t distribution approach those of the standard normal distribution.
Consider a random sample of size n = 31, with sample mean
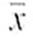 = 45.2 and sample standard deviation s = 5.3.
= 45.2 and sample standard deviation s = 5.3.(a) Compute 90%, 95%, and 99% confidence intervals for using Method 1 with a Student's t distribution. Round endpoints to two digits after the decimal.
(b) Compute 90%, 95%, and 99% confidence intervals for using Method 2 with the standard normal distribution. Use s as an estimate for . Round endpoints to two digits after the decimal.
(c) Compare intervals for the two methods. Would you say that confidence intervals using a Student's t distribution are more conservative in the sense that they tend to be longer than intervals based on the standard normal distribution
(d) Repeat parts (a) through (c) for a sample of size n = 81. With increased sample size, do the two methods give respective confidence intervals that are more similar
Explanation
Given that sample size n = 31 and sample...
Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


