Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics
expand icon
book Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase cover

Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase

Edition 6ISBN: 978-1111827021
book Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase cover

Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase

Edition 6ISBN: 978-1111827021
Exercise 50
Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the
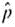Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by 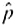and q by 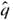= 1 - 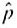. Then we require that n 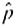5 and n 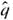5. Show that the conditions n 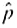5 and n 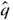5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 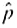5, replace 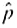by r/n and solve for r. In the inequality n 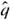5, replace 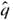by ( n - r )/ n and solve for n - r. 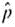distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by
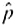Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by and q by = 1 - . Then we require that n 5 and n 5. Show that the conditions n 5 and n 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 5, replace by r/n and solve for r. In the inequality n 5, replace by ( n - r )/ n and solve for n - r. and q by
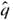Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by and q by = 1 - . Then we require that n 5 and n 5. Show that the conditions n 5 and n 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 5, replace by r/n and solve for r. In the inequality n 5, replace by ( n - r )/ n and solve for n - r. = 1 -
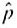Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by and q by = 1 - . Then we require that n 5 and n 5. Show that the conditions n 5 and n 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 5, replace by r/n and solve for r. In the inequality n 5, replace by ( n - r )/ n and solve for n - r. . Then we require that n
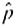Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by and q by = 1 - . Then we require that n 5 and n 5. Show that the conditions n 5 and n 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 5, replace by r/n and solve for r. In the inequality n 5, replace by ( n - r )/ n and solve for n - r. 5 and n
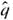Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by and q by = 1 - . Then we require that n 5 and n 5. Show that the conditions n 5 and n 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 5, replace by r/n and solve for r. In the inequality n 5, replace by ( n - r )/ n and solve for n - r. 5. Show that the conditions n
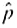Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by and q by = 1 - . Then we require that n 5 and n 5. Show that the conditions n 5 and n 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 5, replace by r/n and solve for r. In the inequality n 5, replace by ( n - r )/ n and solve for n - r. 5 and n
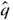Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by and q by = 1 - . Then we require that n 5 and n 5. Show that the conditions n 5 and n 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 5, replace by r/n and solve for r. In the inequality n 5, replace by ( n - r )/ n and solve for n - r. 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n
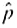Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by and q by = 1 - . Then we require that n 5 and n 5. Show that the conditions n 5 and n 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 5, replace by r/n and solve for r. In the inequality n 5, replace by ( n - r )/ n and solve for n - r. 5, replace
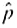Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by and q by = 1 - . Then we require that n 5 and n 5. Show that the conditions n 5 and n 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 5, replace by r/n and solve for r. In the inequality n 5, replace by ( n - r )/ n and solve for n - r. by r/n and solve for r. In the inequality n
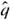Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by and q by = 1 - . Then we require that n 5 and n 5. Show that the conditions n 5 and n 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 5, replace by r/n and solve for r. In the inequality n 5, replace by ( n - r )/ n and solve for n - r. 5, replace
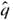Critical Thinking: Brain Teaser A requirement for using the normal distribution to approximate the distribution is that both np 5 and nq 5. Since we usually do not known p , we estimate p by and q by = 1 - . Then we require that n 5 and n 5. Show that the conditions n 5 and n 5 are equivalent to the condition that out of n binomial trails, both the number of successes r and the number of failures n - r must exceed 5. Hint: In the inequality n 5, replace by r/n and solve for r. In the inequality n 5, replace by ( n - r )/ n and solve for n - r. by ( n - r )/ n and solve for n - r.
Explanation
Verified
like image
like image
like image

We are to show that
blured image and
blured image , both grea...

close menu
Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase
cross icon

Why don’t you like this exercise?

Other
Minimum 8 character and maximum 255 character
Character 255
Examlex
Examlex
Work With Us
Policies
Download the App
Scan to downloadDownload the App
qr-code
Links
Links
Work With Us
Download the App

Scan to downloadDownload the App
qr-code

Copyright © 2025 Examlex LLC.
  • facebook-footer
  • instagram-footer
  • x-footer
  • tiktok
  • Linktree