
Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase
Edition 6ISBN: 978-1111827021
Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase
Edition 6ISBN: 978-1111827021 Exercise 40
Expand Your Knowledge: Confidence Intervals and Two-Tailed Hypothesis Test Is there a relationship between confidence intervals and two-tailed hypothesis tests Let c be the level of confidence used to construct a confidence interval from sample data. Let be the level of significance for a two-tailed hypothesis test. The following statement applies to hypothesis tests of the mean.
For a two-tailed hypothesis test with level of significance and null hypothesis H 0 : = k , we reject H 0 whenever k falls outside the c = 1 - confidence interval for based on the sample data. When k falls within the c = 1 - confidence interval, we do not reject H 0.
(A corresponding relationship between confidence intervals and two-tailed hypothesis tests also is valid for other parameters, such as p , 1 2 , and p 1 p 2 , which we will study in Sections 9.3, 10.2, and 10.3.) Whenever the value of k given in the null hypothesis falls outside the c = 1 - confidence interval for the parameter, we reject H 0. For example, consider a two-tailed hypothesis test with = 0.01 and
H 0 : = 20 H 1 : 20
A random sample of size 36 has a sample mean
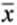 = 22 from a population with standard deviation = 4.
= 22 from a population with standard deviation = 4.
(a) What is the value of c = 1 Using the methods of Chapter 8, construct a 1 confidence interval for from the sample data. What is the value of given in the null hypothesis (i.e., what is k ) Is this value in the confidence interval Do we reject or fail to reject H 0 based on this information
(b) Using methods of this chapter, find the P -value for the hypothesis test. Do we reject or fail to reject H 0 Compare your result to that part (a).
For a two-tailed hypothesis test with level of significance and null hypothesis H 0 : = k , we reject H 0 whenever k falls outside the c = 1 - confidence interval for based on the sample data. When k falls within the c = 1 - confidence interval, we do not reject H 0.
(A corresponding relationship between confidence intervals and two-tailed hypothesis tests also is valid for other parameters, such as p , 1 2 , and p 1 p 2 , which we will study in Sections 9.3, 10.2, and 10.3.) Whenever the value of k given in the null hypothesis falls outside the c = 1 - confidence interval for the parameter, we reject H 0. For example, consider a two-tailed hypothesis test with = 0.01 and
H 0 : = 20 H 1 : 20
A random sample of size 36 has a sample mean
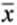 = 22 from a population with standard deviation = 4.
= 22 from a population with standard deviation = 4.(a) What is the value of c = 1 Using the methods of Chapter 8, construct a 1 confidence interval for from the sample data. What is the value of given in the null hypothesis (i.e., what is k ) Is this value in the confidence interval Do we reject or fail to reject H 0 based on this information
(b) Using methods of this chapter, find the P -value for the hypothesis test. Do we reject or fail to reject H 0 Compare your result to that part (a).
Explanation
(a)
We are given that
=22,
=4, and...
Understanding Basic Statistics 6th Edition by Charles Henry Brase,Corrinne Pellillo Brase
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


