Chat with AI
Microeconomic Theory 11th Edition by Walter Nicholson,Christopher Snyder
Edition 11ISBN: 978-1111525538Microeconomic Theory 11th Edition by Walter Nicholson,Christopher Snyder
Edition 11ISBN: 978-1111525538 Exercise 1
Suppose
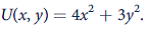
a. Calculate
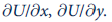
b. Evaluate these partial derivatives at x = 1, y = 2.
c. Write the total differential for U.
d. Calculate dy/dx for dU = 0-that is, what is the implied trade-off between x and y holding U constant?
e. Show U = 16 when x = 1, y = 2.
f. In what ratio must x and y change to hold U constant at 16 for movements away from x = 1, y = 2?
g. More generally, what is the shape of the U = 16 contour line for this function? What is the slope of that line?
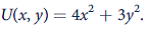
a. Calculate
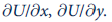
b. Evaluate these partial derivatives at x = 1, y = 2.
c. Write the total differential for U.
d. Calculate dy/dx for dU = 0-that is, what is the implied trade-off between x and y holding U constant?
e. Show U = 16 when x = 1, y = 2.
f. In what ratio must x and y change to hold U constant at 16 for movements away from x = 1, y = 2?
g. More generally, what is the shape of the U = 16 contour line for this function? What is the slope of that line?
Explanation
Verified
Verified
Utility function: It refers to a function use to measure the consumer's level of satisfaction derives from the consumption of goods and services.
The utility function is given by,
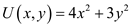a.
Given the utility function, the partial differentiation with respect to a single variable, in a function of several variables is calculated as follows;
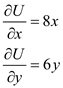b.
Partial differentiation with respect to x is
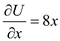and with respect to y is
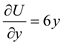. Compute partial derivatives at x= 1 and y = 2 by substituting the values of x and y in the above partial derivates computed in previous part. It is computed below:
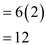c.
Total differentiation is written with the help of partial differentiation.
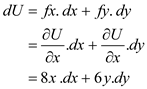d.
Total differentiation is written with the help of partial differentiation.
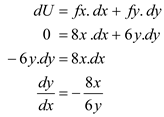So,
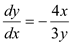It means trade-off between x and y is not linear. The negative sign shows that getting more x required forgoing some y and vice-versa.
e.
To prove that value of U is 16, when
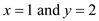, substitute the value of x and y in the utility function and solve as follows:
Hence, the value of utility is 16.
f.
To determine the change in ratio of x and y while holding utility constant at 16, substitute the value of x and y in the
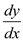computed in part d. It is computed below:
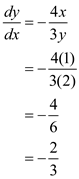Hence, (-2/3) ratio of x and y needed to hold U constant at 16.
g.
To plot the utility function, compute the horizontal and the vertical corner points as follows:
Vertical points: When x is 0, then y will be,
Thus, vertical point is (0,2.30)
Horizontal points: When y is 0, then x will be,
Thus, horizontal point is (2,0).
The following figure shows the shape of utility function when utility is 16:
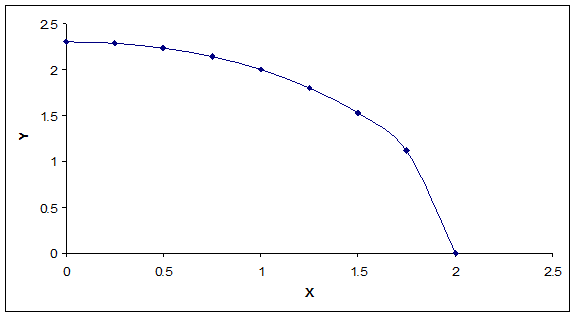As shown in the above figure, the shape of U is an ellipse centered at the origin.
Slope of this equation is
.
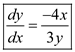The utility function is given by,
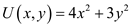a. Given the utility function, the partial differentiation with respect to a single variable, in a function of several variables is calculated as follows;
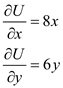b. Partial differentiation with respect to x is
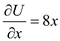and with respect to y is 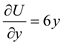. Compute partial derivatives at x= 1 and y = 2 by substituting the values of x and y in the above partial derivates computed in previous part. It is computed below: 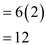c. Total differentiation is written with the help of partial differentiation.
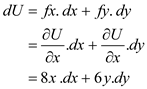d. Total differentiation is written with the help of partial differentiation.
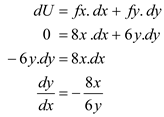So,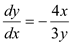 It means trade-off between x and y is not linear. The negative sign shows that getting more x required forgoing some y and vice-versa.e.
To prove that value of U is 16, when
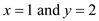, substitute the value of x and y in the utility function and solve as follows: Hence, the value of utility is 16. f.
To determine the change in ratio of x and y while holding utility constant at 16, substitute the value of x and y in the
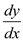computed in part d. It is computed below: 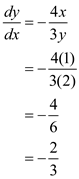Hence, (-2/3) ratio of x and y needed to hold U constant at 16.g.
To plot the utility function, compute the horizontal and the vertical corner points as follows:
Vertical points: When x is 0, then y will be, Thus, vertical point is (0,2.30)Horizontal points: When y is 0, then x will be,
Thus, horizontal point is (2,0). The following figure shows the shape of utility function when utility is 16:
As shown in the above figure, the shape of U is an ellipse centered at the origin.Slope of this equation is
.
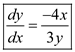Microeconomic Theory 11th Edition by Walter Nicholson,Christopher Snyder
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255
