Chat with AI
Business Forecasting 9th Edition by John Hanke, Dean Wichern
Edition 9ISBN: 978-0132301206Business Forecasting 9th Edition by John Hanke, Dean Wichern
Edition 9ISBN: 978-0132301206 Exercise 1
ALCAM ELECTRONICS
Jarrick Tilby recently received a degree in business administration from a small university and went to work for Alcam Electronics, a manufacturer of various electronic components for industry. After a few weeks on the job, he was called into the office of Alcam's owner and manager, McKennah Labrum, who asked him to investigate a question regarding a certain transistor manufactured by Alcam because a large TV company was interested in a major purchase.
McKennah wanted to forecast the average lifetime of this type of transistor, a matter of great concern to the TV company. Units currently in stock could represent those that would be produced over the lifetime of the new contract, should it be accepted.
Jarrick decided to take a random sample of the transistors in question and formulated a plan to accomplish this task. He numbered the storage bins holding the transistors, drew random bin numbers, and sampled all transistors in each selected bin for the sample. Since each bin contained about 20 transistors, he selected 10 random numbers, which gave him a final sample size of 205 transistors. Because he had selected 10 of 55 bins, he thought he had a good representative sample and could use the results of this sample to generalize to the entire population of transistors in inventory as well as to units yet to be manufactured by the same process.
Jarrick then considered the question of the average lifetime of the units. Because the unit's lifetime can extend to several years, he realized that none of the sampled units could be tested if a timely answer was desired. Therefore, he decided to contact several users of this component to determine if any lifetime records were available. Fortunately, he found three companies that had used the transistor in the past and that had limited records on component lifetimes. In total, he received data on 38 transistors whose failure times were known. Since these transistors were manufactured using the current process, he reasoned that the results of this sample could be used to make inferences about the units in inventory and those yet to be produced.
The results of the computations Jarrick performed on his sample of lifetime data follow.
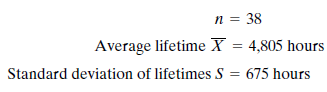
After finding that the sample average lifetime was only 4,805 hours, Jarrick was concerned because he knew the other supplier of components was guaranteeing an average lifetime of 5,000 hours. Although his sample average was a bit below 5,000 hours, he realized that the sample size was only 38 and that this did not constitute positive proof that Alcam's quality was inferior to that of the other supplier. He decided to test the hypothesis that the average lifetime of all transistors was 5,000 hours against the alternative that it was less. Following are the calculations he performed using ? =.01:
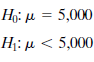
If S = 675, then the decision point is
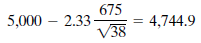
and the decision rule is as follows:
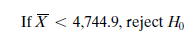
Since the sample mean (4,805) was not below the decision rule point for rejection (4,744.9), Jarrick failed to reject the hypothesis that the mean lifetime of all components was equal to 5,000 hours. He thought this would be good news to McKennah Labrum and included a summary of his findings in his final report. A few days after he gave his written and verbal report to her, McKennah called him into her office to compliment him on a good job and to share a concern she had regarding his findings. She said, "I am concerned about the very low significance level of your hypothesis test. You took only a 1% chance of rejecting the null hypothesis if it is true. This strikes me as very conservative. I am concerned that we will enter into a contract and then find that our quality level does not meet the desired 5,000-hour specification."
How would you respond to McKennah Labrum's comment?
Jarrick Tilby recently received a degree in business administration from a small university and went to work for Alcam Electronics, a manufacturer of various electronic components for industry. After a few weeks on the job, he was called into the office of Alcam's owner and manager, McKennah Labrum, who asked him to investigate a question regarding a certain transistor manufactured by Alcam because a large TV company was interested in a major purchase.
McKennah wanted to forecast the average lifetime of this type of transistor, a matter of great concern to the TV company. Units currently in stock could represent those that would be produced over the lifetime of the new contract, should it be accepted.
Jarrick decided to take a random sample of the transistors in question and formulated a plan to accomplish this task. He numbered the storage bins holding the transistors, drew random bin numbers, and sampled all transistors in each selected bin for the sample. Since each bin contained about 20 transistors, he selected 10 random numbers, which gave him a final sample size of 205 transistors. Because he had selected 10 of 55 bins, he thought he had a good representative sample and could use the results of this sample to generalize to the entire population of transistors in inventory as well as to units yet to be manufactured by the same process.
Jarrick then considered the question of the average lifetime of the units. Because the unit's lifetime can extend to several years, he realized that none of the sampled units could be tested if a timely answer was desired. Therefore, he decided to contact several users of this component to determine if any lifetime records were available. Fortunately, he found three companies that had used the transistor in the past and that had limited records on component lifetimes. In total, he received data on 38 transistors whose failure times were known. Since these transistors were manufactured using the current process, he reasoned that the results of this sample could be used to make inferences about the units in inventory and those yet to be produced.
The results of the computations Jarrick performed on his sample of lifetime data follow.
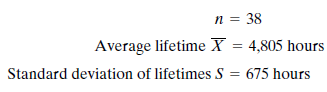
After finding that the sample average lifetime was only 4,805 hours, Jarrick was concerned because he knew the other supplier of components was guaranteeing an average lifetime of 5,000 hours. Although his sample average was a bit below 5,000 hours, he realized that the sample size was only 38 and that this did not constitute positive proof that Alcam's quality was inferior to that of the other supplier. He decided to test the hypothesis that the average lifetime of all transistors was 5,000 hours against the alternative that it was less. Following are the calculations he performed using ? =.01:
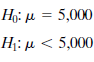
If S = 675, then the decision point is
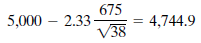
and the decision rule is as follows:
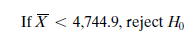
Since the sample mean (4,805) was not below the decision rule point for rejection (4,744.9), Jarrick failed to reject the hypothesis that the mean lifetime of all components was equal to 5,000 hours. He thought this would be good news to McKennah Labrum and included a summary of his findings in his final report. A few days after he gave his written and verbal report to her, McKennah called him into her office to compliment him on a good job and to share a concern she had regarding his findings. She said, "I am concerned about the very low significance level of your hypothesis test. You took only a 1% chance of rejecting the null hypothesis if it is true. This strikes me as very conservative. I am concerned that we will enter into a contract and then find that our quality level does not meet the desired 5,000-hour specification."
How would you respond to McKennah Labrum's comment?
Explanation
Verified
Verified
Explanation:
From the given case, it is clear that Jarrick Tilby's risk taking attitude is too conservative. In the result, he had concluded that there is no evidence to reject the null hypothesis at the low level of significance (1%). That is, the average lifetime of all transistors was 5,000 hours.
Consider the case with the level of significance as (5%). That is,
.
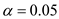Compute the test statistic ( Z ) by using the formula given below:
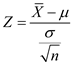Substitute
,
,
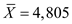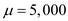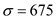, and
.
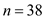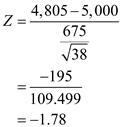Thus, the value of test statistic ( Z ) is
.
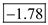Compute the p -value.
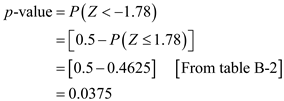Here,
.
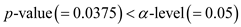Thus, by the decision rule, reject the null hypothesis. Therefore, it is clear that for the significance level 0.05 (greater than 0.01), the null hypothesis is rejected. Hence, it can be concluded that the average lifetime of all transistors is less than 5,000 hours.
However, for the low level of significance (0.01), the company may be put in a bad position as it insists on very notable evidence that the average lifetime of all transistors was 5,000 hours.
From the given case, it is clear that Jarrick Tilby's risk taking attitude is too conservative. In the result, he had concluded that there is no evidence to reject the null hypothesis at the low level of significance (1%). That is, the average lifetime of all transistors was 5,000 hours.
Consider the case with the level of significance as (5%). That is,
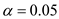.Compute the test statistic ( Z ) by using the formula given below:
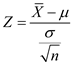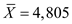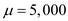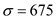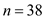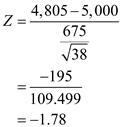Substitute , , , and . Thus, the value of test statistic ( Z ) is 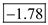.Compute the p -value.
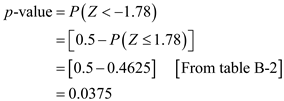Here, 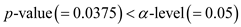.Thus, by the decision rule, reject the null hypothesis. Therefore, it is clear that for the significance level 0.05 (greater than 0.01), the null hypothesis is rejected. Hence, it can be concluded that the average lifetime of all transistors is less than 5,000 hours.
However, for the low level of significance (0.01), the company may be put in a bad position as it insists on very notable evidence that the average lifetime of all transistors was 5,000 hours.
Business Forecasting 9th Edition by John Hanke, Dean Wichern
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255
