
College Physics 10th Edition by Raymond Serway,Chris Vuille
Edition 10ISBN: 978-1285737041
College Physics 10th Edition by Raymond Serway,Chris Vuille
Edition 10ISBN: 978-1285737041 Exercise 1
A small sphere of mass m = 7.50 g and charge q 1 = 32.0 nC is attached to the end of a string and hangs vertically as in Figure P15.4. A second charge of equal mass and charge q 2 = 258.0 nC is located below the first charge a distance d = 2.00 cm below the first charge as in Figure P15.4. (a) Find the tension in the string. (b) If the string can withstand a maximum tension of 0.180 N, what is the smallest value d can have before the string breaks
Explanation
(a)
Coulomb's law states that the electro static force between the two charges is directly proportional to the charge of each particle and inversely proportional to the square of the distance between the two charges. Here,
Here,  is the Coulomb's constant,
is the Coulomb's constant,  is the charge of the particle 1,
is the charge of the particle 1, 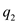 is the charge of the particle 2, and
is the charge of the particle 2, and 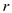 is the distance between the two particles.
is the distance between the two particles.
Substitute for
for  ,
, 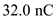 for
for  ,
, 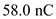 for
for 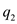 , and
, and 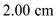 for
for 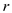 .
.  The tension T in the string is pointed in an upward direction and the gravitational force
The tension T in the string is pointed in an upward direction and the gravitational force  is pointed in a downward direction. The electrical Coulomb force
is pointed in a downward direction. The electrical Coulomb force  exerted by the lower charge is in downward direction. Thus, the net force exerted on the system when it is in equilibrium.
exerted by the lower charge is in downward direction. Thus, the net force exerted on the system when it is in equilibrium. 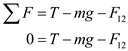 Here,
Here, 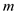 is the mass of each particle and
is the mass of each particle and 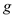 is the acceleration due to gravity.
is the acceleration due to gravity.
Rewrite the equation for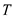 .
. 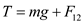 Substitute
Substitute 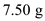 for
for 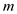 ,
, 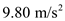 for
for 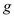 , and
, and 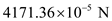 for
for  .
.  Therefore, the tension in the string is
Therefore, the tension in the string is 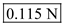 .
.
(b)
Let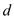 be the new distance between the two charges and
be the new distance between the two charges and 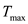 be the maximum tension in the string. Thus, the net force exerted on the system is,
be the maximum tension in the string. Thus, the net force exerted on the system is,  Rewrite the equation for
Rewrite the equation for 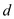 .
.  Substitute
Substitute 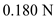 for
for 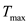 ,
, 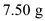 for
for 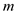 ,
, 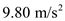 for
for 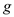 ,
,  for
for  ,
, 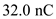 for
for  , and
, and 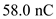 for
for 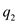 .
.  Therefore, the smallest value of distance d possible before the string breaks is
Therefore, the smallest value of distance d possible before the string breaks is 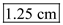 .
.
Coulomb's law states that the electro static force between the two charges is directly proportional to the charge of each particle and inversely proportional to the square of the distance between the two charges.
 Here,
Here,  is the Coulomb's constant,
is the Coulomb's constant,  is the charge of the particle 1,
is the charge of the particle 1, 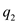 is the charge of the particle 2, and
is the charge of the particle 2, and 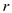 is the distance between the two particles.
is the distance between the two particles.Substitute
 for
for  ,
, 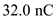 for
for  ,
, 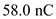 for
for 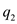 , and
, and 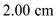 for
for 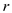 .
.  The tension T in the string is pointed in an upward direction and the gravitational force
The tension T in the string is pointed in an upward direction and the gravitational force  is pointed in a downward direction. The electrical Coulomb force
is pointed in a downward direction. The electrical Coulomb force  exerted by the lower charge is in downward direction. Thus, the net force exerted on the system when it is in equilibrium.
exerted by the lower charge is in downward direction. Thus, the net force exerted on the system when it is in equilibrium. 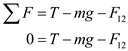 Here,
Here, 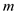 is the mass of each particle and
is the mass of each particle and 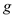 is the acceleration due to gravity.
is the acceleration due to gravity.Rewrite the equation for
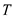 .
. 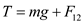 Substitute
Substitute 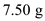 for
for 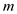 ,
, 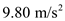 for
for 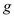 , and
, and 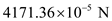 for
for  .
.  Therefore, the tension in the string is
Therefore, the tension in the string is 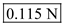 .
. (b)
Let
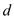 be the new distance between the two charges and
be the new distance between the two charges and 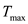 be the maximum tension in the string. Thus, the net force exerted on the system is,
be the maximum tension in the string. Thus, the net force exerted on the system is,  Rewrite the equation for
Rewrite the equation for 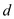 .
.  Substitute
Substitute 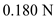 for
for 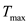 ,
, 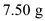 for
for 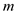 ,
, 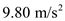 for
for 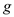 ,
,  for
for  ,
, 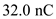 for
for  , and
, and 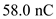 for
for 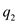 .
.  Therefore, the smallest value of distance d possible before the string breaks is
Therefore, the smallest value of distance d possible before the string breaks is 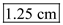 .
.College Physics 10th Edition by Raymond Serway,Chris Vuille
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


