
Optical Fiber Communications 4th Edition by Gerd Keiser
Edition 4ISBN: 978-0073380711
Optical Fiber Communications 4th Edition by Gerd Keiser
Edition 4ISBN: 978-0073380711 Exercise 10
Recall from Eq. (7.13) that the bit-error rate (BER) can be given in terms of a Q factor, where, from Eq. (7.14), 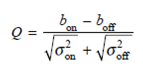
When thermal noise is dominant, we have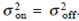 . However, for an EDFA the existence of signal-ASE beat noise produces the condition
. However, for an EDFA the existence of signal-ASE beat noise produces the condition 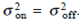 . In this case,
. In this case, 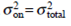 from Eq. (11.30),
from Eq. (11.30), 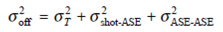
and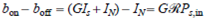
Noting that the receiver sensitivity P R is half the signal power of a transmitted 1 bit for a uniform distribution of ones and zeros (i.e., P s = 2 P R ), show that in terms of the Q factor the receiver sensitivity is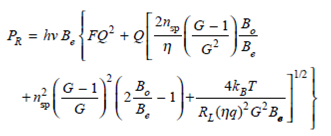
where F is the noise figure given by Eq. (11.35).
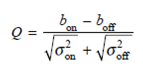
When thermal noise is dominant, we have
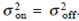 . However, for an EDFA the existence of signal-ASE beat noise produces the condition
. However, for an EDFA the existence of signal-ASE beat noise produces the condition 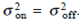 . In this case,
. In this case, 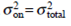 from Eq. (11.30),
from Eq. (11.30), 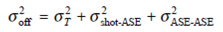
and
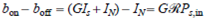
Noting that the receiver sensitivity P R is half the signal power of a transmitted 1 bit for a uniform distribution of ones and zeros (i.e., P s = 2 P R ), show that in terms of the Q factor the receiver sensitivity is
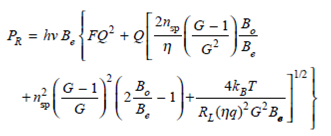
where F is the noise figure given by Eq. (11.35).
Explanation
Substituting the various expressions for...
Optical Fiber Communications 4th Edition by Gerd Keiser
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


