
An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Edition 13ISBN: 978-1439043271
An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Edition 13ISBN: 978-1439043271 Exercise 26
Digital Controls, Inc. (DCI), manufactures two models of a radar gun used by police to monitor the speed of automobiles. Model A has an accuracy of plus or minus 1 mile per hour, whereas the smaller model B has an accuracy of plus or minus 3 miles per hour. For the next week, the company has orders for 100 units of model A and 150 units of model B. Although DCI purchases all the electronic components used in both models, the plastic cases for both models are manufactured at a DCI plant in Newark, New Jersey. Each model A case requires 4 minutes of injection-molding time and 6 minutes of assembly time. Each model B case requires 3 minutes of injection-molding time and 8 minutes of assembly time. For next week, the Newark plant has 600 minutes of injection-molding time available at the Newark plant, DCI occasionally purchases cases for one or both models from an outside supplier in order to fill customer orders that could not be filled otherwise. The purchase cost is $14 for each model A case and $9 for each model B case. Management wants to develop a minimum cost plan that will determined how many cases of each model should be produced at the Newark plant and how many cases of each model should be purchased. The following decision variables were used to formulate a linear programming model for this problem: 
The linear programming model that can be used to solve this problem is as follows:
The computer solution is shown in Figure 3.18.
a. What is the optimal solution and what is the optimal value of the objective function?
b. Which constraints are binding?
c. What are the dual values? Interpret each.
d. If you could change the right-hand side of one constraint by one unit, which one would you choose? Why?
FIGURE 3.18 THE SOLUTION FOR THE DIGITAL CONTROLS, INC., PROBLEM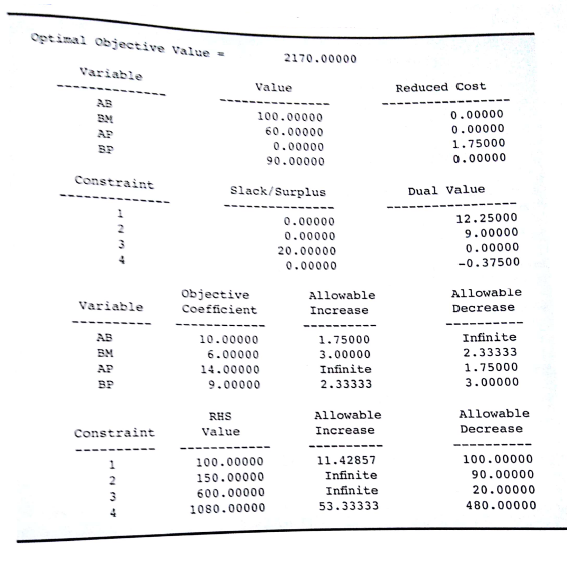

The linear programming model that can be used to solve this problem is as follows:

The computer solution is shown in Figure 3.18.
a. What is the optimal solution and what is the optimal value of the objective function?
b. Which constraints are binding?
c. What are the dual values? Interpret each.
d. If you could change the right-hand side of one constraint by one unit, which one would you choose? Why?
FIGURE 3.18 THE SOLUTION FOR THE DIGITAL CONTROLS, INC., PROBLEM

Explanation
Linear Programming
Linear programming i...
An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


