Chat with AI
An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Edition 13ISBN: 978-1439043271An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Edition 13ISBN: 978-1439043271 Exercise 22
The purpose of this exercise is to learn how to calculate stock returns for portfolio models using actual stock price data. First, it is necessary to obtain stock price data. One source (of many) is Yahoo! Go to the link http://finance.yahoo.com and type in a ticker symbol such as AAPL (for Apple Computer). Then on the left-hand side of the page, select Historical Data.
These data easily downloaded to a spreadsheet by clicking on the link Download to Spreadsheet at the bottom of the page. For Apple Computer (AAPL), Advanced Micro Devices (AMD), and Oracle Corporation (ORCL), download the monthly price data January 1997 through January 2006. These data contain closing prices that are adjusted for stock dividends and splits.
You now have stock prices for 10 years and the objective is to calculate the annual returns for each stock for the years 1997 through 2005. Returns are often calculated using continuous compounding. If the stock prices are adjusted for splits and stock dividends, then the price of stock i in period t + 1, P i,t +1 , is given by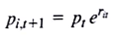
where p it is the price of stock i in period t and r it is the return on stock i in period t. This calculation assumes no cash dividends were paid, which is true of Apple Computer. Advanced Micro Devices, and Oracle Corporation. Solving the equation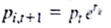
for the return on stock i in period t gives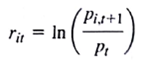 
For example, the Apple Computer adjusted closing price in January 2005 was 38.45. The closing price in January 2006 was 75.51. Thus, the continuously compounded return for Apple Computer from January 2005 to January 2006 is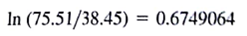
We use this calculation as our estimate of the annual return for Apple Computer for the year 2005.
Take the closing stock prices that you have downloaded and calculate the annual returns for 1997-2005 for AAPL, AMD, and ORCL using r it = ln ( p i,t +1 / p t ). If you calculate the returns properly, your results should appear as in Figure 8.15.
FIGURE 8.15 YEARLY RETURNS FOR AAPL, AMD, AND ORCL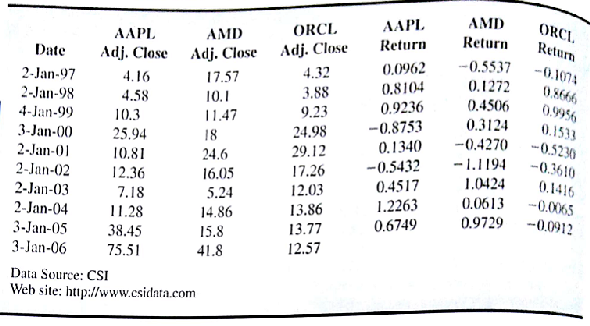
These data easily downloaded to a spreadsheet by clicking on the link Download to Spreadsheet at the bottom of the page. For Apple Computer (AAPL), Advanced Micro Devices (AMD), and Oracle Corporation (ORCL), download the monthly price data January 1997 through January 2006. These data contain closing prices that are adjusted for stock dividends and splits.
You now have stock prices for 10 years and the objective is to calculate the annual returns for each stock for the years 1997 through 2005. Returns are often calculated using continuous compounding. If the stock prices are adjusted for splits and stock dividends, then the price of stock i in period t + 1, P i,t +1 , is given by
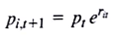
where p it is the price of stock i in period t and r it is the return on stock i in period t. This calculation assumes no cash dividends were paid, which is true of Apple Computer. Advanced Micro Devices, and Oracle Corporation. Solving the equation
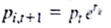for the return on stock i in period t gives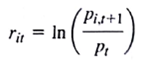 For example, the Apple Computer adjusted closing price in January 2005 was 38.45. The closing price in January 2006 was 75.51. Thus, the continuously compounded return for Apple Computer from January 2005 to January 2006 is
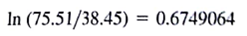
We use this calculation as our estimate of the annual return for Apple Computer for the year 2005.
Take the closing stock prices that you have downloaded and calculate the annual returns for 1997-2005 for AAPL, AMD, and ORCL using r it = ln ( p i,t +1 / p t ). If you calculate the returns properly, your results should appear as in Figure 8.15.
FIGURE 8.15 YEARLY RETURNS FOR AAPL, AMD, AND ORCL
Explanation
This question doesn’t have an expert verified answer yet, let Examlex AI Copilot help.
An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255
