
An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Edition 13ISBN: 978-1439043271
An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Edition 13ISBN: 978-1439043271 Exercise 4
Most investors are happy when their returns are "above average," but not so happy when they are "below average." In the Markowitz portfolio optimization problem given by equations (8.10) through (8.19), the objective function is to minimize variance, which is given by 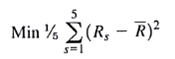
where R s is the portfolio return under scenario s and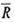 is the expected or average return of the portfolio.
is the expected or average return of the portfolio.
With this objective function, we are choosing a portfolio that minimizes deviations both above and below the average,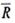 . However, most investors are happy when
. However, most investors are happy when 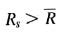 ), but unhappy when R s R. With this preference in mind, an alternative to the variance measure in the objective function for the Markowitz model is the semivariance. The semivariance is calculated by only considering deviations below
), but unhappy when R s R. With this preference in mind, an alternative to the variance measure in the objective function for the Markowitz model is the semivariance. The semivariance is calculated by only considering deviations below 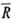 .
.
Let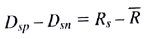 , and restrict D sp and D sn to be nonnegative. Then D sp measures the positive deviation from the mean return in scenario s (i.e.,
, and restrict D sp and D sn to be nonnegative. Then D sp measures the positive deviation from the mean return in scenario s (i.e., 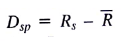 when
when 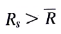 ). In the case where the scenario return is below the average return,
). In the case where the scenario return is below the average return, 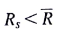 , we have
, we have 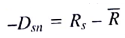 . Using these new variables, we can reformulate the Markowitz model to minimize only the square of negative deviations below the average return. By doing so, we will use the semivariance rather than the variance in the objective function.
. Using these new variables, we can reformulate the Markowitz model to minimize only the square of negative deviations below the average return. By doing so, we will use the semivariance rather than the variance in the objective function.
Reformulate the Markowitz portfolio optimization model given in equations (8.10) through (8.19) to use semivariance in the objective function. Solve assume ? of the portfolio is allocated to each mutual fund for a starting solution.
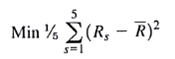
where R s is the portfolio return under scenario s and
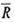 is the expected or average return of the portfolio.
is the expected or average return of the portfolio.With this objective function, we are choosing a portfolio that minimizes deviations both above and below the average,
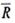 . However, most investors are happy when
. However, most investors are happy when 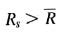 ), but unhappy when R s R. With this preference in mind, an alternative to the variance measure in the objective function for the Markowitz model is the semivariance. The semivariance is calculated by only considering deviations below
), but unhappy when R s R. With this preference in mind, an alternative to the variance measure in the objective function for the Markowitz model is the semivariance. The semivariance is calculated by only considering deviations below 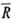 .
.Let
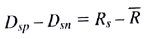 , and restrict D sp and D sn to be nonnegative. Then D sp measures the positive deviation from the mean return in scenario s (i.e.,
, and restrict D sp and D sn to be nonnegative. Then D sp measures the positive deviation from the mean return in scenario s (i.e., 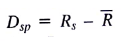 when
when 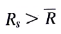 ). In the case where the scenario return is below the average return,
). In the case where the scenario return is below the average return, 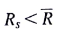 , we have
, we have 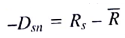 . Using these new variables, we can reformulate the Markowitz model to minimize only the square of negative deviations below the average return. By doing so, we will use the semivariance rather than the variance in the objective function.
. Using these new variables, we can reformulate the Markowitz model to minimize only the square of negative deviations below the average return. By doing so, we will use the semivariance rather than the variance in the objective function.Reformulate the Markowitz portfolio optimization model given in equations (8.10) through (8.19) to use semivariance in the objective function. Solve assume ? of the portfolio is allocated to each mutual fund for a starting solution.
Explanation

This question doesn’t have an expert verified answer yet, let Examlex AI Copilot help.
An Introduction to Management Science 13th Edition by David Anderson,Dennis Sweeney ,Thomas Williams ,Jeffrey Camm, Kipp Martin
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


