
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Edition 4ISBN: 978-0324660609
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Edition 4ISBN: 978-0324660609 Exercise 3
Let Y 1 , Y 2 , Y 3 , and Y 4 be independent, identically distributed random variables from a population with mean and variance 2. Let 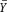 =
= 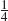 (Y 1 +Y 2 + Y 3 + Y 4 ) denote the average of these four random variables.
(Y 1 +Y 2 + Y 3 + Y 4 ) denote the average of these four random variables.
(i) What are the expected value and variance of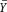 P in terms of and 2
P in terms of and 2
(ii) Now, consider a different estimator of :
W =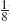 Y 1 +
Y 1 + 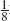 Y 2 +
Y 2 + 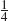 Y 3 +
Y 3 + 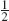 Y 4.
Y 4.
This is an example of a weighted average of the Yi. Show that W is also an unbiased estimator of . Find the variance of W.
(iii) Based on your answers to parts (i) and (ii), which estimator of do you prefer,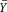 or W
or W
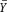 =
= 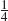 (Y 1 +Y 2 + Y 3 + Y 4 ) denote the average of these four random variables.
(Y 1 +Y 2 + Y 3 + Y 4 ) denote the average of these four random variables.(i) What are the expected value and variance of
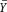 P in terms of and 2
P in terms of and 2 (ii) Now, consider a different estimator of :
W =
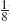 Y 1 +
Y 1 + 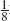 Y 2 +
Y 2 + 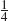 Y 3 +
Y 3 + 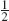 Y 4.
Y 4.This is an example of a weighted average of the Yi. Show that W is also an unbiased estimator of . Find the variance of W.
(iii) Based on your answers to parts (i) and (ii), which estimator of do you prefer,
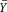 or W
or WExplanation
The following variables are random and i...
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


