Chat with AI
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Edition 4ISBN: 978-0324660609Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Edition 4ISBN: 978-0324660609 Exercise 2
Let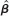 
be the (k + 1) × 1 vector of OLS estimates.
(i) Show that for any (k + 1) × 1 vector b, we can write the sum of squared residuals as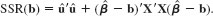
(ii) Explain how the expression for SSR(b) in part (i) proves that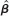
uniquely minimizes SSR(b) over all possible values of b, assuming X has rank k + 1.
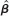be the (k + 1) × 1 vector of OLS estimates.(i) Show that for any (k + 1) × 1 vector b, we can write the sum of squared residuals as
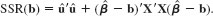
(ii) Explain how the expression for SSR(b) in part (i) proves that
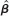uniquely minimizes SSR(b) over all possible values of b, assuming X has rank k + 1.Explanation
Verified
Verified
Consider 
be the vector of OLS estimate...
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255
