
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Edition 4ISBN: 978-0324660609
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Edition 4ISBN: 978-0324660609 Exercise 5
Consider the standard simple regression model y = 0 + 1 x + u under the Gauss-Markov Assumptions SLR.l through SLR.5. The usual OLS estimators 30 and J3X are unbiased for their respective population parameters. Let 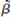 1 be the estimator of 1 obtained by assuming the intercept is zero (see Section 2.6).
1 be the estimator of 1 obtained by assuming the intercept is zero (see Section 2.6).
(i) Find E(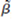 1 ) in terms of the x, 0 , and 1. Verify that
1 ) in terms of the x, 0 , and 1. Verify that 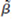 1 is unbiased for 1 when the population intercept ( 0 ) is zero. Are there other cases where 1 is unbiased
1 is unbiased for 1 when the population intercept ( 0 ) is zero. Are there other cases where 1 is unbiased
(ii) Find the variance of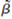 1. (Hint: The variance does not depend on 1.)
1. (Hint: The variance does not depend on 1.) 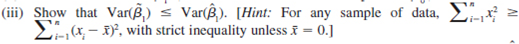 (iv)Comment on the trade off between bias and variance when choosing between
(iv)Comment on the trade off between bias and variance when choosing between 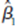 and
and 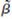 .
.
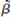 1 be the estimator of 1 obtained by assuming the intercept is zero (see Section 2.6).
1 be the estimator of 1 obtained by assuming the intercept is zero (see Section 2.6).(i) Find E(
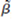 1 ) in terms of the x, 0 , and 1. Verify that
1 ) in terms of the x, 0 , and 1. Verify that 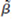 1 is unbiased for 1 when the population intercept ( 0 ) is zero. Are there other cases where 1 is unbiased
1 is unbiased for 1 when the population intercept ( 0 ) is zero. Are there other cases where 1 is unbiased (ii) Find the variance of
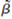 1. (Hint: The variance does not depend on 1.)
1. (Hint: The variance does not depend on 1.) 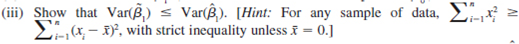 (iv)Comment on the trade off between bias and variance when choosing between
(iv)Comment on the trade off between bias and variance when choosing between 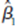 and
and 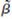 .
.Explanation
i)
To show the unbiasedness of the regre...
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
Why don’t you like this exercise?
Other Minimum 8 character and maximum 255 character
Character 255


