Campbell Biology 11th Edition by Lisa Urry,Michael Cain,Steven Wasserman,Peter Minorsky,Jane Reece

Exercise 9

Calibrating a Standard Radioactive Isotope Decay Curve and Interpreting Data
How Long Might Neanderthals Have Co-Existed with Modern Humans ( Homo sapiens ) Neanderthals ( Homo neanderthalensis ) were living in Europe by 350,000 years ago and may have coexisted with early Homo sapiens in parts of Eurasia for hundreds or thousands of years before Neanderthals became extinct. Researchers sought to more accurately determine the extent of their overlap by pinning down the latest date Neanderthals still lived in the area. They used carbon-14 dating to determine the age of a Neanderthal fossil from the most recent (uppermost) archeological layer containing Neanderthal bones. In this exercise you will calibrate a standard carbon-14 decay curve and use it to determine the age of this Neanderthal fossil. The age will help you approximate the last time the two species may have coexisted at the site where this fossil was collected.
How the Experiment Was Done Carbon-14 ( ¹⁴C) is a radioactive isotope of carbon that decays to ¹⁴N at a constant rate. ¹⁴C is present in the atmosphere in small amounts at a constant ratio with both ¹³C and ¹²C, two other isotopes of carbon. When carbon is taken up from the atmosphere by a plant during photosynthesis, ¹²C, ¹³C, and ¹⁴C isotopes are incorporated into the plant in the same proportions in which they were present in the atmosphere. These proportions remain the same in the tissues of an animal that eats the plant. While an organism is alive, the ¹⁴C in its body constantly decays to ¹⁴N but is constantly replaced by new carbon from the environment. Once an organism dies, it stops taking in new ¹⁴C but the ¹⁴C in its tissues continues to decay, while the ¹²C in its tissues remains the same because it is not radioactive and does not decay. Thus, scientists can calculate how long the pool of original ¹⁴C has been decaying in a fossil by measuring the ratio of ¹⁴C to ¹²C and comparing it to the ratio of ¹⁴C to ¹²C present originally in the atmosphere. The fraction of ¹⁴C in a fossil compared to the original fraction of ¹⁴C can be converted to years because we know that the half-life of ¹⁴C is 5,730 years-in other words, half of the ¹⁴C in a fossil decays every 5,730 years.
Data from the Experiment The researchers found that the Neanderthal fossil had approximately 0.0078 (or, in scientific notation, 7.8 × 10³ ) as much ¹⁴C as the atmosphere. The following questions will guide you through translating this fraction into the age of the fossil.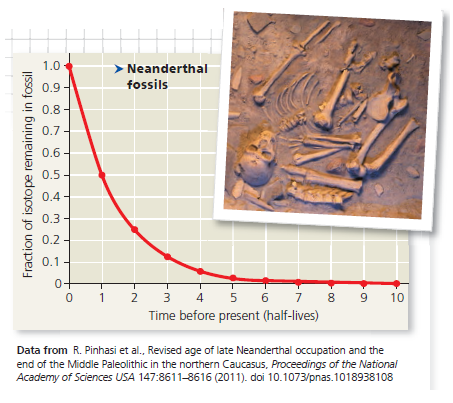
A standard curve of radioactive isotope decay is shown at the top of the right column. The graph line shows the fraction of the radioactive isotope over time (before present) in units of halflives. Recall that a half-life is the amount of time it takes for half of the radioactive isotope to decay. Labeling each data point with the corresponding fractions will help orient you to this graph. Draw an arrow to the data point for half-life = 1 and write the fraction of ¹⁴C that will remain after one half-life. Calculate the fraction of ¹⁴C remaining at each half-life and write the fractions on the graph near arrows pointing to the data points. Convert each fraction to a decimal number and round off to a maximum of three significant digits (zeros at the beginning of the number do not count as significant digits). Also write each decimal number in scientific notation.