Deck 6: Equity: Concepts and Techniques
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/12
Play
Full screen (f)
Deck 6: Equity: Concepts and Techniques
1
Consider Company A with a zero earnings retention ratio and a real growth rate in earnings of
%. In an inflationary environment, the company can only pass inflation through its earnings
at a flow-through rate of %. So if I is the inflation rate, its earnings will grow at a rate of
g = + I. The real rate of return required for this company is , so the nominal rate of return required is r== + I.
Use a simple dividend discount model (DDM) assuming that dividends will grow indefinitely at a constant compounded annual growth rate (CAGR), g = + I.
a. Derive formulas equivalent of Equations (6.7) and (6.8), which assumed no real growth in earnings. Discuss the results.
b. Use these formulas to calculate P/E ratio on prospective earnings with the following data on Company A: = 2%, I = 4%, = 4%, = 100%.
c. Same question for a Company B, whose inflation pass-through rate is only 80%.
%. In an inflationary environment, the company can only pass inflation through its earnings
at a flow-through rate of %. So if I is the inflation rate, its earnings will grow at a rate of
g = + I. The real rate of return required for this company is , so the nominal rate of return required is r== + I.
Use a simple dividend discount model (DDM) assuming that dividends will grow indefinitely at a constant compounded annual growth rate (CAGR), g = + I.
a. Derive formulas equivalent of Equations (6.7) and (6.8), which assumed no real growth in earnings. Discuss the results.
b. Use these formulas to calculate P/E ratio on prospective earnings with the following data on Company A: = 2%, I = 4%, = 4%, = 100%.
c. Same question for a Company B, whose inflation pass-through rate is only 80%.
a. Earnings will grow at a rate + I, assumed constant over time. For example, we have: By discounting this perpetual stream of growing earnings at the required rate, r, we find that the intrinsic value of such a firm would then be: (6.7a)
where P0 is the intrinsic value
E0 is the initial earnings level
is the real growth rate in earnings
I is the annual inflation rate
is the pass-through rate
r is the (nominal) required rate of return.
Of course, r is a nominal rate that includes the rate of inflation. If we introduce the real required rate of return = r- I, we get:
P0 =E0 * The intrinsic P/E using prospective earnings is now equal to:
P0/E1 = . (6.8a)
From Equation (6.8a) we can see that the higher the inflation flow-through rate, the higher the price of the company. Indeed, a company that cannot pass inflation through its earnings is penalized. The higher the inflation rate, the more negative the influence on the stock price if full inflation pass-through cannot be achieved. Irrespective of inflation, the higher the real growth rate, the higher the P/E.
b. Company A earnings will grow at a rate of + I = 2% +100% * 4% = 6%. The P/E will be
P/E =
= 50.
c. Company B cannot fully pass inflation to its earnings. Its P/E is equal to:
P/E(B) = =35.7.
In the inflationary environment, Company B's earnings cannot grow as fast as inflation. Penalized by inflation and its inability to pass along inflation, Company B's price/earnings ratio is below that of Company A.
where P0 is the intrinsic value
E0 is the initial earnings level
is the real growth rate in earnings
I is the annual inflation rate
is the pass-through rate
r is the (nominal) required rate of return.
Of course, r is a nominal rate that includes the rate of inflation. If we introduce the real required rate of return = r- I, we get:
P0 =E0 * The intrinsic P/E using prospective earnings is now equal to:
P0/E1 = . (6.8a)
From Equation (6.8a) we can see that the higher the inflation flow-through rate, the higher the price of the company. Indeed, a company that cannot pass inflation through its earnings is penalized. The higher the inflation rate, the more negative the influence on the stock price if full inflation pass-through cannot be achieved. Irrespective of inflation, the higher the real growth rate, the higher the P/E.
b. Company A earnings will grow at a rate of + I = 2% +100% * 4% = 6%. The P/E will be
P/E =
= 50.
c. Company B cannot fully pass inflation to its earnings. Its P/E is equal to:
P/E(B) = =35.7.
In the inflationary environment, Company B's earnings cannot grow as fast as inflation. Penalized by inflation and its inability to pass along inflation, Company B's price/earnings ratio is below that of Company A.
2
You invest in a country named Papaf. You observe the stock returns on a list of stocks during
three periods.
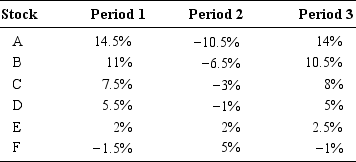 You consider explaining differences in returns by common factors, with a linear model as represented in Equation (6.9). You have two candidates for factors: movements in interest rates and changes in the local temperature measured at noon-time from the previous day. The various values of these factors are given below:
You consider explaining differences in returns by common factors, with a linear model as represented in Equation (6.9). You have two candidates for factors: movements in interest rates and changes in the local temperature measured at noon-time from the previous day. The various values of these factors are given below:
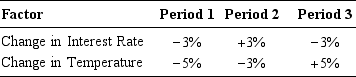 a. Try to assess whether each factor has an influence on stock returns.
a. Try to assess whether each factor has an influence on stock returns.
b. Try to estimate the intercept and the factor exposures of each asset.
three periods.
 You consider explaining differences in returns by common factors, with a linear model as represented in Equation (6.9). You have two candidates for factors: movements in interest rates and changes in the local temperature measured at noon-time from the previous day. The various values of these factors are given below:
You consider explaining differences in returns by common factors, with a linear model as represented in Equation (6.9). You have two candidates for factors: movements in interest rates and changes in the local temperature measured at noon-time from the previous day. The various values of these factors are given below: a. Try to assess whether each factor has an influence on stock returns.
a. Try to assess whether each factor has an influence on stock returns.b. Try to estimate the intercept and the factor exposures of each asset.
a. The model is: 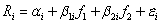 where:
where: 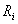 is the return on stock i
is the return on stock i 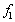 is the factor "change in interest rate"
is the factor "change in interest rate" 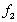 is the factor "change in temperature"
is the factor "change in temperature" 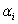 is the intercept of stock i
is the intercept of stock i 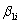 is the exposure of stock i to factor 1
is the exposure of stock i to factor 1 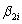 is the exposure of stock i to factor 2.
is the exposure of stock i to factor 2.
We could use a regression to estimate the exposures. A casual look at the data suggests that the second factor has no (or little) influence on stock returns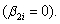 b. The intercept and exposure to the first factor are estimated approximately at:
b. The intercept and exposure to the first factor are estimated approximately at: 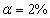 for all stocks
for all stocks 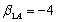
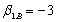
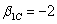
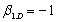
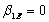
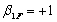
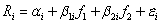 where:
where: 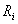 is the return on stock i
is the return on stock i 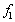 is the factor "change in interest rate"
is the factor "change in interest rate" 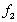 is the factor "change in temperature"
is the factor "change in temperature" 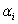 is the intercept of stock i
is the intercept of stock i 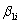 is the exposure of stock i to factor 1
is the exposure of stock i to factor 1 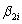 is the exposure of stock i to factor 2.
is the exposure of stock i to factor 2.We could use a regression to estimate the exposures. A casual look at the data suggests that the second factor has no (or little) influence on stock returns
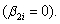 b. The intercept and exposure to the first factor are estimated approximately at:
b. The intercept and exposure to the first factor are estimated approximately at: 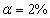 for all stocks
for all stocks 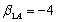
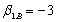
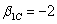
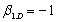
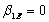
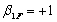
3
You invest in a country named Paf. You consider explaining the difference in returns by two common factors, with a linear factor model as given in Equation (6.9). Your candidate for factors are movements in interest rates and changes in the popularity of the president of Paf, as measured by polls. The various values of the factor returns and of the returns on four stocks (A, B, C, and D) for the ten past periods are given below:
You will try to assess whether the two factors have an influence on stock returns. To do so:
a. Estimate the factor exposures for each of the four assets. (You can do a times-series regression for each asset against the two factors.)
b. Are the factors «priced», that is, is there a relation between mean returns on the assets and their factor exposures? (You can do a cross-sectional regression between the mean return on the asset and its exposures, that is, you have one observation for each asset.)
You will try to assess whether the two factors have an influence on stock returns. To do so:
a. Estimate the factor exposures for each of the four assets. (You can do a times-series regression for each asset against the two factors.)
b. Are the factors «priced», that is, is there a relation between mean returns on the assets and their factor exposures? (You can do a cross-sectional regression between the mean return on the asset and its exposures, that is, you have one observation for each asset.)
a. We estimate the factor exposures for each stock by running a multiple regression between the stock returns and the two factors' returns: where: is the return on stock i is the factor "movements in interest rate" is the factor "change in popularity" is the intercept of stock i is the exposure of stock i to factor 1 is the exposure of stock i to factor 2
The first line gives the mean return of each stock over the ten periods. The next lines give the estimated coefficients of the regressions and their standard errors. It appears that the interest
rate factor has a strong influence on stock returns, and the estimates are highly significant (low standard errors). The exposures to the popularity factor are smaller and much less significant statistically. All R-squares are quite large (above 90%).
b. The second question asked is whether the risk factors are priced. In other words, is there a link between the risk exposures of an asset and its return? If a risk factor is priced, assets with different risk exposures should have different mean returns. This is a cross-sectional conclusion that can be tested by running a regression between the mean return on each stock and their risk exposures. Here we have four observations (four different stocks) and two factors, the cross-sectional regression can be written as:
The two factors are priced. Their slopes are statistically significant, especially for the first factor. The higher the risk exposure to each factor, the higher the mean stock return. However, you should note that the first factor has much more importance in stock pricing. This is because the risk exposures to the first factor vary between 0.77 and 1.94, while the risk exposures to the second factor only vary between -0.23 and 0.07.
The first line gives the mean return of each stock over the ten periods. The next lines give the estimated coefficients of the regressions and their standard errors. It appears that the interest
rate factor has a strong influence on stock returns, and the estimates are highly significant (low standard errors). The exposures to the popularity factor are smaller and much less significant statistically. All R-squares are quite large (above 90%).
b. The second question asked is whether the risk factors are priced. In other words, is there a link between the risk exposures of an asset and its return? If a risk factor is priced, assets with different risk exposures should have different mean returns. This is a cross-sectional conclusion that can be tested by running a regression between the mean return on each stock and their risk exposures. Here we have four observations (four different stocks) and two factors, the cross-sectional regression can be written as:
The two factors are priced. Their slopes are statistically significant, especially for the first factor. The higher the risk exposure to each factor, the higher the mean stock return. However, you should note that the first factor has much more importance in stock pricing. This is because the risk exposures to the first factor vary between 0.77 and 1.94, while the risk exposures to the second factor only vary between -0.23 and 0.07.
4
A company can generate an return on equity (ROE) of 12% and has an earnings retention ratio of 0.80. Next year's earnings are projected at $100 million. If the required rate of return for the company is 10%, what is the company's tangible P/E value, franchise factor, growth factor, and franchise
P/E value?
P/E value?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
5
A company has 500,000 shares outstanding at $20 per share. To its management, the company grants employee stock options on 10,000 shares. Five thousand of these options can be exercised at a price of $21 any time during the next five years. For five years, the employees thus have the right but not the obligation to purchase shares at the $21 price, regardless of the prevailing market price of the stock. Another 5,000 of these options can be exercised at a price of $25 any time during the next
five years. For five years, the employees thus have the right but not the obligation to purchase shares at the $25 price, regardless of the prevailing market price of the stock. The company's auditor can provide an estimate of the options' value. Using price volatility estimates for the stock, a standard Black-Scholes' valuation model gives an estimated value of $12 per share option with an exercise price of $21 and of $7 per share option with an exercise price of $25. Without expensing the options, the company's pretax earnings are reported as $10 million.
a. What are the pretax earnings per share without expensing the share options granted?
b. What are the pretax earnings per share with expensing the share options granted?
five years. For five years, the employees thus have the right but not the obligation to purchase shares at the $25 price, regardless of the prevailing market price of the stock. The company's auditor can provide an estimate of the options' value. Using price volatility estimates for the stock, a standard Black-Scholes' valuation model gives an estimated value of $12 per share option with an exercise price of $21 and of $7 per share option with an exercise price of $25. Without expensing the options, the company's pretax earnings are reported as $10 million.
a. What are the pretax earnings per share without expensing the share options granted?
b. What are the pretax earnings per share with expensing the share options granted?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
6
The U.S. Department of Justice (DoJ) uses the Herfindahl Index to evaluate the impact of a proposed horizontal merger between firms on the degree of market concentration. The following text is an extract of the official document found in 2003 on the DoJ Web site:
Market concentration is a function of the number of firms in a market and their respective market shares. As an aid to the interpretation of market data, the Agency will use the Herfindahl-Hirschman Index ("HHI") of market concentration. The HHI is calculated by summing the squares of the individual market shares of all the participants […].
The Agency divides the spectrum of market concentration as measured by the HHI into three regions that can be broadly characterized as unconcentrated (HHI below 1,000), moderately concentrated (HHI between 1,000 and 1,800), and highly concentrated (HHI above 1,800). Although the resulting regions provide a useful framework for merger analysis, the numerical divisions suggest greater precision than is possible with the available economic tools and information. Other things being equal, cases falling just above and just below a threshold present comparable competitive issues.
1.51 General Standards
In evaluating horizontal mergers, the Agency will consider both the post-merger market concentration and the increase in concentration resulting from the merger. Market concentration is a useful indicator of the likely potential competitive effect of a merger. The general standards for horizontal mergers are as follows:
a. Post-Merger HHI below 0.10. The Agency regards markets in this region to be unconcentrated. Mergers resulting in unconcentrated markets are unlikely to have adverse competitive effects and ordinarily require no further analysis.
b. Post-Merger HHI between 0.10 and 0.18. The Agency regards markets in this region to be moderately concentrated. Mergers producing an increase in the HHI of less than 0.01 points in moderately concentrated markets, post-mergers are unlikely to have adverse competitive consequences and ordinarily require no further analysis. Mergers producing an increase in the HHI of more than 0.01 points in moderately concentrated markets, post-mergers potentially raise significant competitive concerns depending on the factors set forth in
Market concentration is a function of the number of firms in a market and their respective market shares. As an aid to the interpretation of market data, the Agency will use the Herfindahl-Hirschman Index ("HHI") of market concentration. The HHI is calculated by summing the squares of the individual market shares of all the participants […].
The Agency divides the spectrum of market concentration as measured by the HHI into three regions that can be broadly characterized as unconcentrated (HHI below 1,000), moderately concentrated (HHI between 1,000 and 1,800), and highly concentrated (HHI above 1,800). Although the resulting regions provide a useful framework for merger analysis, the numerical divisions suggest greater precision than is possible with the available economic tools and information. Other things being equal, cases falling just above and just below a threshold present comparable competitive issues.
1.51 General Standards
In evaluating horizontal mergers, the Agency will consider both the post-merger market concentration and the increase in concentration resulting from the merger. Market concentration is a useful indicator of the likely potential competitive effect of a merger. The general standards for horizontal mergers are as follows:
a. Post-Merger HHI below 0.10. The Agency regards markets in this region to be unconcentrated. Mergers resulting in unconcentrated markets are unlikely to have adverse competitive effects and ordinarily require no further analysis.
b. Post-Merger HHI between 0.10 and 0.18. The Agency regards markets in this region to be moderately concentrated. Mergers producing an increase in the HHI of less than 0.01 points in moderately concentrated markets, post-mergers are unlikely to have adverse competitive consequences and ordinarily require no further analysis. Mergers producing an increase in the HHI of more than 0.01 points in moderately concentrated markets, post-mergers potentially raise significant competitive concerns depending on the factors set forth in

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
7
In 1989, Jaguar Plc, an English company, was listed on the London SEAQ and on NASDAQ. At the time, one-fourth of Jaguar common stock was held in the form of American Deposit Receipts (ADRs) quoted on NASDAQ. Under U.K. accounting principles, Jaguar reported a 1988 net income (before extraordinary items) of £61 million, a decrease of 27% from 1987 net income. Under U.S. generally accepted accounting principles (GAAP), Jaguar reported a 1988 net income (before extraordinary items) of £113 million, an increase of 89% over the comparable figure for 1987. What would your reaction be as an investor?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
8
Japanese companies tend to belong to groups ("keiretsu") and to hold shares of one another. Because these cross-holdings are minority interests, they tend not to be consolidated in published financial statements. To study the impact of this tradition on published earnings, take the following simplified example:
Company A owns 20% of Company B; the initial investment was 20 billion yen.
Company B owns 30% of Company A; the initial investment was 20 billion yen.
Both companies value their minority interests at historical cost. The year-end nonconsolidated balance sheets of the two companies follow:
The annual net income of Company A was 15 billion yen. The annual net income of Company B was 40 billion yen. Assume that the two companies do not pay any dividends. The current stock market values are 250 billion yen for Company A and 550 billion yen for Company B.
a. Restate the earnings of the two companies, using the equity method of consolidation. Remember that the share of the minority-interest profits is consolidated on a one-line basis, proportionate to the share of the equity owned by the parent. The value of the investment in the subsidiary is adjusted to reflect the change in the subsidiary's equity.
b. Calculate the P/E ratios based on nonconsolidated and consolidated earnings. Are they similar?
Company A owns 20% of Company B; the initial investment was 20 billion yen.
Company B owns 30% of Company A; the initial investment was 20 billion yen.
Both companies value their minority interests at historical cost. The year-end nonconsolidated balance sheets of the two companies follow:
The annual net income of Company A was 15 billion yen. The annual net income of Company B was 40 billion yen. Assume that the two companies do not pay any dividends. The current stock market values are 250 billion yen for Company A and 550 billion yen for Company B.
a. Restate the earnings of the two companies, using the equity method of consolidation. Remember that the share of the minority-interest profits is consolidated on a one-line basis, proportionate to the share of the equity owned by the parent. The value of the investment in the subsidiary is adjusted to reflect the change in the subsidiary's equity.
b. Calculate the P/E ratios based on nonconsolidated and consolidated earnings. Are they similar?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
9
Consider two companies based in a country with an inflation rate of 2%. There is no real growth in earnings. The real rate of return required by global investors for this type of stock investment is 5%.
a. Assume that the Company A can only pass 60% of inflation through its earnings. What should be its P/E using prospective earnings?
b. Assume that the Company B can pass the full inflation through its earnings. What should be its P/E using prospective earnings?
a. Assume that the Company A can only pass 60% of inflation through its earnings. What should be its P/E using prospective earnings?
b. Assume that the Company B can pass the full inflation through its earnings. What should be its P/E using prospective earnings?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
10
You are an active British stock portfolio manager. Your performance is measured against the FTSE index, a broadly based British stock index. It has been repeatedly observed that small-capitalization stocks outperform large-capitalization stocks over prolonged periods of time ("small-firm effect")
but that there have been periods when the reverse was true. It has also been repeatedly observed that value stocks (firms with low price-to-book ratios) outperform growth stocks over prolonged periods of time ("value/growth effect") but that there have been periods when the reverse was true.
How would an attribute factor model be useful in estimating the risks that your performance deviates from that of the assigned benchmark?
but that there have been periods when the reverse was true. It has also been repeatedly observed that value stocks (firms with low price-to-book ratios) outperform growth stocks over prolonged periods of time ("value/growth effect") but that there have been periods when the reverse was true.
How would an attribute factor model be useful in estimating the risks that your performance deviates from that of the assigned benchmark?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
11
In 1993 Daimler-Benz became the first German company to be listed on the New York Stock Exchange (NYSE). This forced Daimler-Benz to file a reconciliation statement with U.S. GAAP (Form 20-F). Because Daimler-Benz drew on hidden reserves during the recession of 1993, its German-reported profit (in Deutsche mark or DM) was a small, but positive, DM615 million. It translated into a DM1.84 billion loss according to U.S. GAAP. Daimler's 1993 net worth translates from DM18.15 billion under German rules to DM26.28 billion under U.S. GAAP.
a. Explain what happened on earnings.
b. Explain what happened on book value (net worth).
c. In a profitable year, Daimler-Benz decides to increase its hidden reserves. How would this decision affect earnings calculated according to U.S. and German GAAP?
d. Same question for book value.
a. Explain what happened on earnings.
b. Explain what happened on book value (net worth).
c. In a profitable year, Daimler-Benz decides to increase its hidden reserves. How would this decision affect earnings calculated according to U.S. and German GAAP?
d. Same question for book value.

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck
12
In studying the impact of consolidation on Price/Earnings (P/E) ratios, there are four basic methods of consolidating the account of a subsidiary into the parent company:
Full consolidation. Assets, liabilities, and earnings of the subsidiaries are fully incorporated,
line-by-line, into the parent's accounts, with special care to avoid double counting.
Proportional consolidation. Assets, liabilities, and earnings are consolidated line-by-line, proportionate to the percentage of ownership in the subsidiary.
Equity consolidation. A share of the subsidiary profits is consolidated on a one-line basis, proportionate to the share of equity owned by the parent. The value of the investment in the subsidiary is adjusted to reflect the change in the subsidiary's equity.
No consolidation. This is sometimes referred to as the cost method, whereby only dividends received from the subsidiary affect earnings of the parent. The value of the investment in the subsidiary is carried at cost in the parent's book and is not revalued.
Here are the simplified 2000 accounts of Papa SA and Fille SA, two French firms. Papa SA owns 50% of Fille SA, a company created the previous year. Fille SA has not paid any dividend. The nonconsolidated accounts follow:
Continued
The nonconsolidated accounts for Papa SA use the cost method, whereby the investment in the subsidiary is carried at historical cost in the balance sheet of the parent.
a. Establish the consolidated accounts, using the other three methods outlined above.
b. Which method provides the highest reported net income for Papa SA?
c. Which method provides the highest P/E ratio, based on book value, for Papa SA?
Full consolidation. Assets, liabilities, and earnings of the subsidiaries are fully incorporated,
line-by-line, into the parent's accounts, with special care to avoid double counting.
Proportional consolidation. Assets, liabilities, and earnings are consolidated line-by-line, proportionate to the percentage of ownership in the subsidiary.
Equity consolidation. A share of the subsidiary profits is consolidated on a one-line basis, proportionate to the share of equity owned by the parent. The value of the investment in the subsidiary is adjusted to reflect the change in the subsidiary's equity.
No consolidation. This is sometimes referred to as the cost method, whereby only dividends received from the subsidiary affect earnings of the parent. The value of the investment in the subsidiary is carried at cost in the parent's book and is not revalued.
Here are the simplified 2000 accounts of Papa SA and Fille SA, two French firms. Papa SA owns 50% of Fille SA, a company created the previous year. Fille SA has not paid any dividend. The nonconsolidated accounts follow:
Continued
The nonconsolidated accounts for Papa SA use the cost method, whereby the investment in the subsidiary is carried at historical cost in the balance sheet of the parent.
a. Establish the consolidated accounts, using the other three methods outlined above.
b. Which method provides the highest reported net income for Papa SA?
c. Which method provides the highest P/E ratio, based on book value, for Papa SA?

Unlock Deck
Unlock for access to all 12 flashcards in this deck.
Unlock Deck
k this deck


