Deck 9: Fundamentals of Hypothesis Testing: One-Sample Tests
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/146
Play
Full screen (f)
Deck 9: Fundamentals of Hypothesis Testing: One-Sample Tests
1
The power of a test is measured by its capability of
A) rejecting a null hypothesis that is true.
B) not rejecting a null hypothesis that is true.
C) rejecting a null hypothesis that is false.
D) not rejecting a null hypothesis that is false.
A) rejecting a null hypothesis that is true.
B) not rejecting a null hypothesis that is true.
C) rejecting a null hypothesis that is false.
D) not rejecting a null hypothesis that is false.
rejecting a null hypothesis that is false.
2
You know that the probability of committing a Type II error (β) is 5%, you can tell that the power of the test is
A) 2.5%.
B) 95%.
C) 97.5%.
D) unknown.
A) 2.5%.
B) 95%.
C) 97.5%.
D) unknown.
95%.
3
If a researcher rejects a true null hypothesis, she has made a ________ error.
Type I
4
If the Type I error (α) for a given test is to be decreased, then for a fixed sample size n
A) the Type II error (β) will also decrease.
B) the Type II error (β) will increase.
C) the power of the test will increase.
D) a one-tail test must be utilized.
A) the Type II error (β) will also decrease.
B) the Type II error (β) will increase.
C) the power of the test will increase.
D) a one-tail test must be utilized.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following would be an appropriate alternative hypothesis?
A) The population proportion is less than 0.65.
B) The sample proportion is less than 0.65.
C) The population proportion is no less than 0.65.
D) The sample proportion is no less than 0.65.
A) The population proportion is less than 0.65.
B) The sample proportion is less than 0.65.
C) The population proportion is no less than 0.65.
D) The sample proportion is no less than 0.65.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
6
If a researcher accepts a false null hypothesis, she has made a ________ error.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following would be an appropriate null hypothesis?
A) The population proportion is less than 0.65.
B) The sample proportion is less than 0.65.
C) The population proportion is no less than 0.65.
D) The sample proportion is no less than 0.65.
A) The population proportion is less than 0.65.
B) The sample proportion is less than 0.65.
C) The population proportion is no less than 0.65.
D) The sample proportion is no less than 0.65.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
8
If a test of hypothesis has a Type I error probability (α) of 0.01, we mean
A) if the null hypothesis is true, we don't reject it 1% of the time.
B) if the null hypothesis is true, we reject it 1% of the time.
C) if the null hypothesis is false, we don't reject it 1% of the time.
D) if the null hypothesis is false, we reject it 1% of the time.
A) if the null hypothesis is true, we don't reject it 1% of the time.
B) if the null hypothesis is true, we reject it 1% of the time.
C) if the null hypothesis is false, we don't reject it 1% of the time.
D) if the null hypothesis is false, we reject it 1% of the time.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
9
If a researcher rejects a false null hypothesis, she has made a ________ decision.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
10
You know that the level of significance (α) of a test is 5%, you can tell that the probability of committing a Type II error (β) is
A) 2.5%.
B) 95%.
C) 97.5%.
D) unknown.
A) 2.5%.
B) 95%.
C) 97.5%.
D) unknown.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
11
Which of the following would be an appropriate null hypothesis?
A) The mean of a population is equal to 55.
B) The mean of a sample is equal to 55.
C) The mean of a population is greater than 55.
D) Only A and C are appropriate.
A) The mean of a population is equal to 55.
B) The mean of a sample is equal to 55.
C) The mean of a population is greater than 55.
D) Only A and C are appropriate.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
12
For a given sample size n, if the level of significance (α) is decreased, the power of the test
A) will increase.
B) will decrease.
C) will remain the same.
D) cannot be determined.
A) will increase.
B) will decrease.
C) will remain the same.
D) cannot be determined.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
13
If an economist wishes to determine whether there is evidence that mean family income in a community equals $50,000
A) either a one-tail or two-tail test could be used with equivalent results.
B) a one-tail test should be utilized.
C) a two-tail test should be utilized.
D) None of the above.
A) either a one-tail or two-tail test could be used with equivalent results.
B) a one-tail test should be utilized.
C) a two-tail test should be utilized.
D) None of the above.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
14
If a researcher accepts a true null hypothesis, she has made a ________ decision.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
15
If an economist wishes to determine whether there is evidence that mean family income in a community exceeds $50,000
A) either a one-tail or two-tail test could be used with equivalent results.
B) a one-tail test should be utilized.
C) a two-tail test should be utilized.
D) None of the above.
A) either a one-tail or two-tail test could be used with equivalent results.
B) a one-tail test should be utilized.
C) a two-tail test should be utilized.
D) None of the above.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following would be an appropriate alternative hypothesis?
A) The mean of a population is equal to 55.
B) The mean of a sample is equal to 55.
C) The mean of a population is greater than 55.
D) The mean of a sample is greater than 55.
A) The mean of a population is equal to 55.
B) The mean of a sample is equal to 55.
C) The mean of a population is greater than 55.
D) The mean of a sample is greater than 55.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
17
For a given level of significance (α), if the sample size n is increased, the probability of a Type II error (β)
A) will decrease.
B) will increase.
C) will remain the same.
D) cannot be determined.
A) will decrease.
B) will increase.
C) will remain the same.
D) cannot be determined.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
18
A Type II error is committed when
A) we reject a null hypothesis that is true.
B) we don't reject a null hypothesis that is true.
C) we reject a null hypothesis that is false.
D) we don't reject a null hypothesis that is false.
A) we reject a null hypothesis that is true.
B) we don't reject a null hypothesis that is true.
C) we reject a null hypothesis that is false.
D) we don't reject a null hypothesis that is false.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
19
A Type I error is committed when
A) we reject a null hypothesis that is true.
B) we don't reject a null hypothesis that is true.
C) we reject a null hypothesis that is false.
D) we don't reject a null hypothesis that is false.
A) we reject a null hypothesis that is true.
B) we don't reject a null hypothesis that is true.
C) we reject a null hypothesis that is false.
D) we don't reject a null hypothesis that is false.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
20
If the p-value is less than α in a two-tail test,
A) the null hypothesis should not be rejected.
B) the null hypothesis should be rejected.
C) a one-tail test should be used.
D) no conclusion should be reached.
A) the null hypothesis should not be rejected.
B) the null hypothesis should be rejected.
C) a one-tail test should be used.
D) no conclusion should be reached.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
21
How many tissues should the Kimberly Clark Corporation package of Kleenex contain? Researchers determined that 60 tissues is the mean number of tissues used during a cold. Suppose a random sample of 100 Kleenex users yielded the following data on the number of tissues used during a cold: 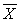 = 52, S = 22. Using the sample information provided, calculate the value of the test statistic.
= 52, S = 22. Using the sample information provided, calculate the value of the test statistic.
A) t = (52 - 60)/22
B) t = (52 - 60)/(22/100)
C) t = (52 - 60)/(22/1002)
D) t = (52 - 60)/(22/10)
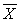 = 52, S = 22. Using the sample information provided, calculate the value of the test statistic.
= 52, S = 22. Using the sample information provided, calculate the value of the test statistic.A) t = (52 - 60)/22
B) t = (52 - 60)/(22/100)
C) t = (52 - 60)/(22/1002)
D) t = (52 - 60)/(22/10)

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
22
The owner of a local nightclub has recently surveyed a random sample of n = 250 customers of the club. She would now like to determine whether or not the mean age of her customers is over 30. If so, she plans to alter the entertainment to appeal to an older crowd. If not, no entertainment changes will be made. Suppose she found that the sample mean was 30.45 years and the sample standard deviation was 5 years. What is the p-value associated with the test statistic?
A) 0.3577
B) 0.1423
C) 0.0780
D) 0.02
A) 0.3577
B) 0.1423
C) 0.0780
D) 0.02

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
23
We have created a 95% confidence interval for μ with the result (10, 15). What decision will we make if we test H0 : μ = 16 versus H1 : μ ≠ 16 at α = 0.10?
A) Reject H0 in favor of H1.
B) Accept H0 in favor of H1.
C) Fail to reject H0 in favor of H1.
D) We cannot tell what our decision will be from the information given.
A) Reject H0 in favor of H1.
B) Accept H0 in favor of H1.
C) Fail to reject H0 in favor of H1.
D) We cannot tell what our decision will be from the information given.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
24
We have created a 95% confidence interval for μ with the result (10, 15). What decision will we make if we test H0 : μ = 16 versus H1 : μ ≠ 16 at α = 0.025?
A) Reject H0 in favor of H1.
B) Accept H0 in favor of H1.
C) Fail to reject H0 in favor of H1.
D) We cannot tell what our decision will be from the information given.
A) Reject H0 in favor of H1.
B) Accept H0 in favor of H1.
C) Fail to reject H0 in favor of H1.
D) We cannot tell what our decision will be from the information given.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
25
If, as a result of a hypothesis test, we reject the null hypothesis when it is false, then we have committed
A) a Type II error.
B) a Type I error.
C) no error.
D) an acceptance error.
A) a Type II error.
B) a Type I error.
C) no error.
D) an acceptance error.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
26
Which of the following statements is not true about the level of significance in a hypothesis test?
A) The larger the level of significance, the more likely you are to reject the null hypothesis.
B) The level of significance is the maximum risk we are willing to accept in making a Type I error.
C) The significance level is also called the α level.
D) The significance level is another name for Type II error.
A) The larger the level of significance, the more likely you are to reject the null hypothesis.
B) The level of significance is the maximum risk we are willing to accept in making a Type I error.
C) The significance level is also called the α level.
D) The significance level is another name for Type II error.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
27
The value that separates a rejection region from a non-rejection region is called the ________.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
28
How many tissues should the Kimberly Clark Corporation package of Kleenex contain? Researchers determined that 60 tissues is the mean number of tissues used during a cold. Suppose a random sample of 100 Kleenex users yielded the following data on the number of tissues used during a cold: = 52, S = 22. Give the null and alternative hypotheses to determine if the number of tissues used during a cold is less than 60. 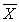
A)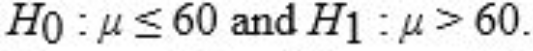
B)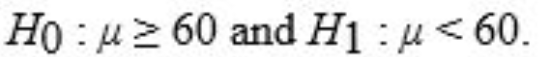
C)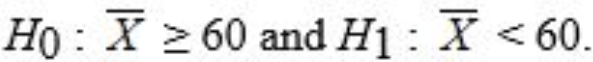
D)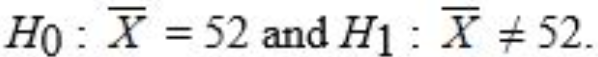
A)
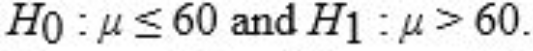
B)
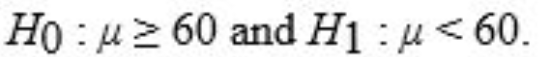
C)
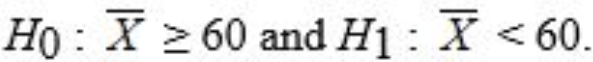
D)
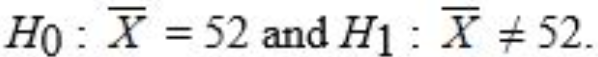

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
29
The owner of a local nightclub has recently surveyed a random sample of n = 250 customers of the club. She would now like to determine whether or not the mean age of her customers is over 30. If so, she plans to alter the entertainment to appeal to an older crowd. If not, no entertainment changes will be made. Suppose she found that the sample mean was 30.45 years and the sample standard deviation was 5 years. If she wants to be 99% confident in her decision, what decision should she make?
A) Reject H0.
B) Accept H0.
C) Fail to reject H0.
D) We cannot tell what her decision should be from the information given.
A) Reject H0.
B) Accept H0.
C) Fail to reject H0.
D) We cannot tell what her decision should be from the information given.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
30
How many tissues should the Kimberly Clark Corporation package of Kleenex contain? Researchers determined that 60 tissues is the mean number of tissues used during a cold. Suppose a random sample of 100 Kleenex users yielded the following data on the number of tissues used during a cold: 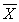 = 52, S = 22. Suppose the alternative we wanted to test was H1 : μ < 60. State the correct rejection region for α = 0.05.
= 52, S = 22. Suppose the alternative we wanted to test was H1 : μ < 60. State the correct rejection region for α = 0.05.
A) Reject H0 if t > 1.6604.
B) Reject H0 if t < -1.6604.
C) Reject H0 if t > 1.9842 or Z < -1.9842.
D) Reject H0 if t < -1.9842.
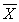 = 52, S = 22. Suppose the alternative we wanted to test was H1 : μ < 60. State the correct rejection region for α = 0.05.
= 52, S = 22. Suppose the alternative we wanted to test was H1 : μ < 60. State the correct rejection region for α = 0.05.A) Reject H0 if t > 1.6604.
B) Reject H0 if t < -1.6604.
C) Reject H0 if t > 1.9842 or Z < -1.9842.
D) Reject H0 if t < -1.9842.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
31
How many tissues should the Kimberly Clark Corporation package of Kleenex contain? Researchers determined that 60 tissues is the mean number of tissues used during a cold. Suppose a random sample of 100 Kleenex users yielded the following data on the number of tissues used during a cold: 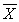 = 52, S = 22. Suppose the test statistic does fall in the rejection region at α = 0.05. Which of the following conclusions is correct?
= 52, S = 22. Suppose the test statistic does fall in the rejection region at α = 0.05. Which of the following conclusions is correct?
A) At α = 0.05, there is not sufficient evidence to conclude that the average number of tissues used during a cold is 60 tissues.
B) At α = 0.05, there is sufficient evidence to conclude that the average number of tissues used during a cold is 60 tissues.
C) At α = 0.05, there is not sufficient evidence to conclude that the average number of tissues used during a cold is not 60 tissues.
D) At α = 0.10, there is sufficient evidence to conclude that the average number of tissues used during a cold is not 60 tissues.
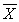 = 52, S = 22. Suppose the test statistic does fall in the rejection region at α = 0.05. Which of the following conclusions is correct?
= 52, S = 22. Suppose the test statistic does fall in the rejection region at α = 0.05. Which of the following conclusions is correct?A) At α = 0.05, there is not sufficient evidence to conclude that the average number of tissues used during a cold is 60 tissues.
B) At α = 0.05, there is sufficient evidence to conclude that the average number of tissues used during a cold is 60 tissues.
C) At α = 0.05, there is not sufficient evidence to conclude that the average number of tissues used during a cold is not 60 tissues.
D) At α = 0.10, there is sufficient evidence to conclude that the average number of tissues used during a cold is not 60 tissues.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
32
We have created a 95% confidence interval for μ with the result (10, 15). What decision will we make if we test H0 : μ = 16 versus H1 : μ ≠ 16 at α = 0.05?
A) Reject H0 in favor of H1.
B) Accept H0 in favor of H1.
C) Fail to reject H0 in favor of H1.
D) We cannot tell what our decision will be from the information given.
A) Reject H0 in favor of H1.
B) Accept H0 in favor of H1.
C) Fail to reject H0 in favor of H1.
D) We cannot tell what our decision will be from the information given.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
33
The symbol for the power of a statistical test is
A) α.
B) 1 - α.
C) β.
D) 1 - β.
A) α.
B) 1 - α.
C) β.
D) 1 - β.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
34
The owner of a local nightclub has recently surveyed a random sample of n = 250 customers of the club. She would now like to determine whether or not the mean age of her customers is over 30. If so, she plans to alter the entertainment to appeal to an older crowd. If not, no entertainment changes will be made. If she wants to be 99% confident in her decision, what rejection region should she use?
A) Reject H0 if t < -2.3263.
B) Reject H0 if t < -2.5758.
C) Reject H0 if t > 2.3263.
D) Reject H0 if t > 2.5758.
A) Reject H0 if t < -2.3263.
B) Reject H0 if t < -2.5758.
C) Reject H0 if t > 2.3263.
D) Reject H0 if t > 2.5758.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
35
How many tissues should the Kimberly Clark Corporation package of Kleenex contain? Researchers determined that 60 tissues is the mean number of tissues used during a cold. Suppose a random sample of 100 Kleenex users yielded the following data on the number of tissues used during a cold: 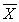 = 52, S = 22. Suppose the test statistic does fall in the rejection region at α = 0.05. Which of the following decisions is correct?
= 52, S = 22. Suppose the test statistic does fall in the rejection region at α = 0.05. Which of the following decisions is correct?
A) At α = 0.05, we do not reject H0.
B) At α = 0.05, we reject H0.
C) At α = 0.05, we accept H0.
D) At α = 0.10, we do not reject H0.
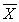 = 52, S = 22. Suppose the test statistic does fall in the rejection region at α = 0.05. Which of the following decisions is correct?
= 52, S = 22. Suppose the test statistic does fall in the rejection region at α = 0.05. Which of the following decisions is correct?A) At α = 0.05, we do not reject H0.
B) At α = 0.05, we reject H0.
C) At α = 0.05, we accept H0.
D) At α = 0.10, we do not reject H0.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
36
Suppose we wish to test H0: μ ≤ 47 versus H1: μ > 47. What will result if we conclude that the mean is greater than 47 when its true value is really 52?
A) We have made a Type I error.
B) We have made a Type II error.
C) We have made a correct decision.
D) None of the above are correct.
A) We have made a Type I error.
B) We have made a Type II error.
C) We have made a correct decision.
D) None of the above are correct.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
37
A ________ is a numerical quantity computed from the data of a sample and is used in reaching a decision on whether or not to reject the null hypothesis.
A) significance level
B) critical value
C) test statistic
D) parameter
A) significance level
B) critical value
C) test statistic
D) parameter

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
38
The owner of a local nightclub has recently surveyed a random sample of n = 250 customers of the club. She would now like to determine whether or not the mean age of her customers is over 30. If so, she plans to alter the entertainment to appeal to an older crowd. If not, no entertainment changes will be made. Suppose she found that the sample mean was 30.45 years and the sample standard deviation was 5 years. If she wants to be 99% confident in her decision, what conclusion can she make?
A) There is not sufficient evidence that the mean age of her customers is over 30.
B) There is sufficient evidence that the mean age of her customers is over 30.
C) There is not sufficient evidence that the mean age of her customers is not over 30.
D) There is sufficient evidence that the mean age of her customers is not over 30.
A) There is not sufficient evidence that the mean age of her customers is over 30.
B) There is sufficient evidence that the mean age of her customers is over 30.
C) There is not sufficient evidence that the mean age of her customers is not over 30.
D) There is sufficient evidence that the mean age of her customers is not over 30.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
39
The power of a statistical test is
A) the probability of not rejecting H0 when it is false.
B) the probability of rejecting H0 when it is true.
C) the probability of not rejecting H0 when it is true.
D) the probability of rejecting H0 when it is false.
A) the probability of not rejecting H0 when it is false.
B) the probability of rejecting H0 when it is true.
C) the probability of not rejecting H0 when it is true.
D) the probability of rejecting H0 when it is false.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
40
It is possible to directly compare the results of a confidence interval estimate to the results obtained by testing a null hypothesis if
A) a two-tail test for μ is used.
B) a one-tail test for μ is used.
C) Both of the previous statements are true.
D) None of the previous statements is true.
A) a two-tail test for μ is used.
B) a one-tail test for μ is used.
C) Both of the previous statements are true.
D) None of the previous statements is true.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
41
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the parameter the manager is interested in is:
A) the mean number of defective light bulbs per case produced at the plant.
B) the mean number of defective light bulbs per case among the 46 cases.
C) the mean number of defective light bulbs per case produced during the morning shift.
D) the proportion of cases with defective light bulbs produced at the plant.
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the parameter the manager is interested in is:
A) the mean number of defective light bulbs per case produced at the plant.
B) the mean number of defective light bulbs per case among the 46 cases.
C) the mean number of defective light bulbs per case produced during the morning shift.
D) the proportion of cases with defective light bulbs produced at the plant.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
42
A survey claims that 9 out of 10 doctors recommend aspirin for their patients with headaches. To test this claim against the alternative that the actual proportion of doctors who recommend aspirin is less than 0.90, a random sample of 100 doctors was selected. Suppose that the test statistic is -2.20. Can we conclude that H0 should be rejected at the (a) α = 0.10, (b) α = 0.05, and (c) α = 0.01 level of Type I error?
A) (a) yes; (b) yes; (c) yes
B) (a) no; (b) no; (c) no
C) (a) no; (b) no; (c) yes
D) (a) yes; (b) yes; (c) no
A) (a) yes; (b) yes; (c) yes
B) (a) no; (b) no; (c) no
C) (a) no; (b) no; (c) yes
D) (a) yes; (b) yes; (c) no

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
43
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the null hypothesis would be rejected if a 1% probability of committing a Type I error is allowed.
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the null hypothesis would be rejected if a 1% probability of committing a Type I error is allowed.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
44
A major DVD rental chain is considering opening a new store in an area that currently does not have any such stores. The chain will open if there is evidence that more than 5,000 of the 20,000 households in the area are equipped with DVD players. It conducts a telephone poll of 300 randomly selected households in the area and finds that 96 have DVD players. The p-value associated with the test statistic in this problem is approximately equal to:
A) 0.0100
B) 0.0051
C) 0.0026
D) 0.0013
A) 0.0100
B) 0.0051
C) 0.0026
D) 0.0013

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
45
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the null hypothesis would be rejected.
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the null hypothesis would be rejected.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
46
A survey claims that 9 out of 10 doctors recommend aspirin for their patients with headaches. To test this claim against the alternative that the actual proportion of doctors who recommend aspirin is less than 0.90, a random sample of 100 doctors results in 83 who indicate that they recommend aspirin. The value of the test statistic in this problem is approximately equal to:
A) -4.12.
B) -2.33.
C) -1.86.
D) -0.07.
A) -4.12.
B) -2.33.
C) -1.86.
D) -0.07.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
47
An entrepreneur is considering the purchase of a coin-operated laundry. The current owner claims that over the past 5 years, the mean daily revenue was $675 with a standard deviation of $75. A sample of 30 days reveals a daily mean revenue of $625. If you were to test the null hypothesis that the daily mean revenue was $675, which test would you use?
A) Z-test of a population mean
B) Z-test of a population proportion
C) t-test of a population mean
D) t-test of a population proportion
A) Z-test of a population mean
B) Z-test of a population proportion
C) t-test of a population mean
D) t-test of a population proportion

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
48
The marketing manager for an automobile manufacturer is interested in determining the proportion of new compact-car owners who would have purchased a side curtain air bag if it had been available for an additional cost of $300. The manager believes from previous information that the proportion is 0.30. Suppose that a survey of 200 new compact-car owners is selected and 79 indicate that they would have purchased the side curtain air bags. If you were to conduct a test to determine whether there is evidence that the proportion is different from 0.30, which test would you use?
A) Z-test of a population mean
B) Z-test of a population proportion
C) t-test of population mean
D) t-test of a population proportion
A) Z-test of a population mean
B) Z-test of a population proportion
C) t-test of population mean
D) t-test of a population proportion

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
49
A major DVD rental chain is considering opening a new store in an area that currently does not have any such stores. The chain will open if there is evidence that more than 5,000 of the 20,000 households in the area are equipped with DVD players. It conducts a telephone poll of 300 randomly selected households in the area and finds that 96 have DVD players. The decision on the hypothesis test using a 3% level of significance is
A) to reject H0 in favor of H1.
B) to accept H0 in favor of H1.
C) to fail to reject H0 in favor of H1.
D) We cannot tell what the decision should be from the information given.
A) to reject H0 in favor of H1.
B) to accept H0 in favor of H1.
C) to fail to reject H0 in favor of H1.
D) We cannot tell what the decision should be from the information given.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
50
The marketing manager for an automobile manufacturer is interested in determining the proportion of new compact-car owners who would have purchased a side curtain air bag if it had been available for an additional cost of $300. The manager believes from previous information that the proportion is 0.30. Suppose that a survey of 200 new compact-car owners is selected and 79 indicate that they would have purchased the side curtain air bags. If you were to conduct a test to determine whether there is evidence that the proportion is different from 0.30 and decided not to reject the null hypothesis, what conclusion could you draw?
A) There is sufficient evidence that the proportion is 0.30.
B) There is not sufficient evidence that the proportion is 0.30.
C) There is sufficient evidence that the proportion is not 0.30.
D) There is not sufficient evidence that the proportion is not 0.30.
A) There is sufficient evidence that the proportion is 0.30.
B) There is not sufficient evidence that the proportion is 0.30.
C) There is sufficient evidence that the proportion is not 0.30.
D) There is not sufficient evidence that the proportion is not 0.30.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
51
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, what critical value should the manager use to determine the rejection region?
A) 1.6794
B) 1.3011
C) 1.3006
D) 0.6800
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, what critical value should the manager use to determine the rejection region?
A) 1.6794
B) 1.3011
C) 1.3006
D) 0.6800

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
52
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the null hypothesis would be rejected if a 5% probability of committing a Type I error is allowed.
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the null hypothesis would be rejected if a 5% probability of committing a Type I error is allowed.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
53
A manager of the credit department for an oil company would like to determine whether the mean monthly balance of credit card holders is equal to $75. An auditor selects a random sample of 100 accounts and finds that the mean owed is $83.40 with a sample standard deviation of $23.65. If you wanted to test whether the auditor should conclude that there is evidence that the mean balance is different from $75, which test would you use?
A) Z-test of a population mean
B) Z-test of a population proportion
C) t-test of a population mean
D) t-test of a population proportion
A) Z-test of a population mean
B) Z-test of a population proportion
C) t-test of a population mean
D) t-test of a population proportion

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
54
A major DVD rental chain is considering opening a new store in an area that currently does not have any such stores. The chain will open if there is evidence that more than 5,000 of the 20,000 households in the area are equipped with DVD players. It conducts a telephone poll of 300 randomly selected households in the area and finds that 96 have DVD players. State the test of interest to the rental chain.
A) H0 : π ≤ 0.32 versus H1 : π > 0.32
B) H0 : π ≤ 0.25 versus H1 : π > 0.25
C) H0 : π ≤ 5,000 versus H1 : π > 5,000
D) H0 : μ ≤ 5,000 versus H1 : μ > 5,000
A) H0 : π ≤ 0.32 versus H1 : π > 0.32
B) H0 : π ≤ 0.25 versus H1 : π > 0.25
C) H0 : π ≤ 5,000 versus H1 : π > 5,000
D) H0 : μ ≤ 5,000 versus H1 : μ > 5,000

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
55
An entrepreneur is considering the purchase of a coin-operated laundry. The current owner claims that over the past 5 years, the mean daily revenue was $675 with a standard deviation of $75. A sample of 30 days reveals a daily mean revenue of $625. If you were to test the null hypothesis that the daily mean revenue was $675 and decide not to reject the null hypothesis, what can you conclude?
A) There is not enough evidence to conclude that the daily mean revenue was $675.
B) There is not enough evidence to conclude that the daily mean revenue was not $675.
C) There is enough evidence to conclude that the daily mean revenue was $675.
D) There is enough evidence to conclude that the daily mean revenue was not $675.
A) There is not enough evidence to conclude that the daily mean revenue was $675.
B) There is not enough evidence to conclude that the daily mean revenue was not $675.
C) There is enough evidence to conclude that the daily mean revenue was $675.
D) There is enough evidence to conclude that the daily mean revenue was not $675.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
56
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, state the alternative hypothesis for this study.
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, state the alternative hypothesis for this study.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
57
A manager of the credit department for an oil company would like to determine whether the mean monthly balance of credit card holders is equal to $75. An auditor selects a random sample of 100 accounts and finds that the mean owed is $83.40 with a sample standard deviation of $23.65. If you were to conduct a test to determine whether the mean balance is different from $75 and decided to reject the null hypothesis, what conclusion could you draw?
A) There is not evidence that the mean balance is $75.
B) There is not evidence that the mean balance is not $75.
C) There is evidence that the mean balance is $75.
D) There is evidence that the mean balance is not $75.
A) There is not evidence that the mean balance is $75.
B) There is not evidence that the mean balance is not $75.
C) There is evidence that the mean balance is $75.
D) There is evidence that the mean balance is not $75.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
58
A survey claims that 9 out of 10 doctors recommend aspirin for their patients with headaches. To test this claim against the alternative that the actual proportion of doctors who recommend aspirin is less than 0.90, a random sample of 100 doctors was selected. Suppose you reject the null hypothesis. What conclusion can you draw?
A) There is not sufficient evidence that the proportion of doctors who recommend aspirin is not less than 0.90.
B) There is sufficient evidence that the proportion of doctors who recommend aspirin is not less than 0.90.
C) There is not sufficient evidence that the proportion of doctors who recommend aspirin is less than 0.90.
D) There is sufficient evidence that the proportion of doctors who recommend aspirin is less than 0.90.
A) There is not sufficient evidence that the proportion of doctors who recommend aspirin is not less than 0.90.
B) There is sufficient evidence that the proportion of doctors who recommend aspirin is not less than 0.90.
C) There is not sufficient evidence that the proportion of doctors who recommend aspirin is less than 0.90.
D) There is sufficient evidence that the proportion of doctors who recommend aspirin is less than 0.90.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
59
A major DVD rental chain is considering opening a new store in an area that currently does not have any such stores. The chain will open if there is evidence that more than 5,000 of the 20,000 households in the area are equipped with DVD players. It conducts a telephone poll of 300 randomly selected households in the area and finds that 96 have DVD players. The value of the test statistic in this problem is approximately equal to:
A) 2.80
B) 2.60
C) 1.94
D) 1.30
A) 2.80
B) 2.60
C) 1.94
D) 1.30

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
60
A major DVD rental chain is considering opening a new store in an area that currently does not have any such stores. The chain will open if there is evidence that more than 5,000 of the 20,000 households in the area are equipped with DVD players. It conducts a telephone poll of 300 randomly selected households in the area and finds that 96 have DVD players. The rental chain's conclusion from the hypothesis test using a 3% level of significance is
A) to open a new store.
B) not to open a new store.
C) to delay opening a new store until additional evidence is collected.
D) We cannot tell what the decision should be from the information given.
A) to open a new store.
B) not to open a new store.
C) to delay opening a new store until additional evidence is collected.
D) We cannot tell what the decision should be from the information given.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
61
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the lowest level of significance at which the null hypothesis can be rejected is ________.
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the lowest level of significance at which the null hypothesis can be rejected is ________.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
62
"Is the intended sample size large enough to achieve the desired power of the test for the level of significance chosen?" should be among the questions asked when performing a hypothesis test.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
63
"What conclusions and interpretations can you reach from the results of the hypothesis test?" is not an important question to ask when performing a hypothesis test.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
64
Suppose, in testing a hypothesis about a proportion, the p-value is computed to be 0.034. The null hypothesis should be rejected if the chosen level of significance is 0.01.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
65
In a hypothesis test, it is irrelevant whether the test is a one-tail or two-tail test.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
66
The statement of the null hypothesis always contains an equality.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
67
Suppose, in testing a hypothesis about a proportion, the p-value is computed to be 0.043. The null hypothesis should be rejected if the chosen level of significance is 0.05.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
68
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the evidence proves beyond a doubt that the mean number of defective bulbs per case is over 20 during the morning shift.
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the evidence proves beyond a doubt that the mean number of defective bulbs per case is over 20 during the morning shift.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
69
In instances in which there is insufficient evidence to reject the null hypothesis, you must make it clear that this has proven that the null hypothesis is true.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
70
A proper methodology in performing hypothesis tests is to ask whether a random sample can be selected from the population of interest.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
71
In instances in which there is insufficient evidence to reject the null hypothesis, you must make it clear that this does not prove that the null hypothesis is true.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
72
In testing a hypothesis, you should always raise the question on the purpose of the study, survey or experiment.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
73
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, if these data were used to perform a two-tail test, the p-value would be 0.042.
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, if these data were used to perform a two-tail test, the p-value would be 0.042.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
74
The test statistic measures how close the computed sample statistic has come to the hypothesized population parameter.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
75
Suppose, in testing a hypothesis about a proportion, the Z test statistic is computed to be 2.04. The null hypothesis should be rejected if the chosen level of significance is 0.01 and a two-tail test is used.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
76
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the manager can conclude that there is sufficient evidence to show that the mean number of defective bulbs per case is over 20 during the morning shift using a level of significance of 0.10.
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the manager can conclude that there is sufficient evidence to show that the mean number of defective bulbs per case is over 20 during the morning shift using a level of significance of 0.10.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
77
In conducting research, you should document both good and bad results.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
78
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the manager can conclude that there is sufficient evidence to show that the mean number of defective bulbs per case is over 20 during the morning shift with no more than a 5% probability of incorrectly rejecting the true null hypothesis.
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the manager can conclude that there is sufficient evidence to show that the mean number of defective bulbs per case is over 20 during the morning shift with no more than a 5% probability of incorrectly rejecting the true null hypothesis.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
79
You should report only the results of hypothesis tests that show statistical significance and omit those for which there is insufficient evidence in the findings.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck
80
TABLE 9-1
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the manager can conclude that there is sufficient evidence to show that the mean number of defective bulbs per case is over 20 during the morning shift with no more than a 1% probability of incorrectly rejecting the true null hypothesis.
Microsoft Excel was used on a set of data involving the number of defective items found in a random sample of 46 cases of light bulbs produced during a morning shift at a plant. A manager wants to know if the mean number of defective bulbs per case is over 20 during the morning shift. She will make her decision using a test with a level of significance of 0.10. The following information was extracted from the Microsoft Excel output for the sample of 46 cases:
n = 46; Arithmetic Mean = 28.00; Standard Deviation = 25.92; Standard Error = 3.82;
Null Hypothesis: H0 : μ ≤ 20.000; α = 0.10; df = 45; T Test Statistic = 2.09;
One-Tail Test Upper Critical Value = 1.3006; p-value = 0.021; Decision = Reject.
Referring to Table 9-1, the manager can conclude that there is sufficient evidence to show that the mean number of defective bulbs per case is over 20 during the morning shift with no more than a 1% probability of incorrectly rejecting the true null hypothesis.

Unlock Deck
Unlock for access to all 146 flashcards in this deck.
Unlock Deck
k this deck


