Deck 3: Topics in Deifferentiation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/171
Play
Full screen (f)
Deck 3: Topics in Deifferentiation
1
Find 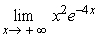 .
.
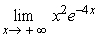 .
.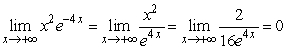
2
Evaluate. 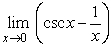 .
.
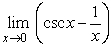 .
.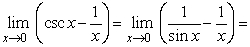
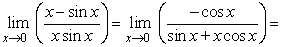 -oo
-oo 3
Answer true or false. 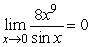
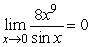
True
4
Evaluate. 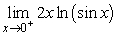 .
.
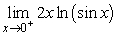 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
5
Answer true or false. 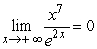
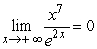

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate. 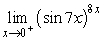
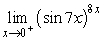

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
7
Evaluate. 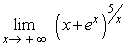
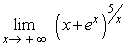

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
8
Answer true or false. 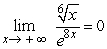 .
.
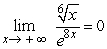 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
9
Evaluate. 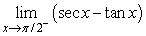
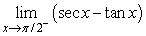

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate. 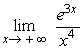 .
.
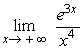 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
11
Evaluate. 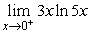 .
.
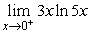 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
12
Evaluate. 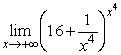
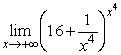

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
13
Evaluate. 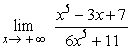 .
.
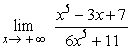 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
14
Answer true or false. 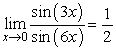 .
.
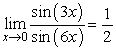 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
15
Answer true or false. 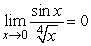 .
.
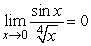 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
16
Evaluate. 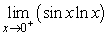 .
.
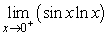 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
17
Evaluate. 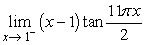 .
.
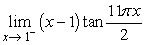 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
18
Evaluate. 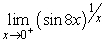
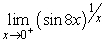

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate. 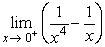 .
.
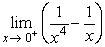 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate. 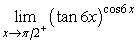 .
.
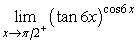 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate. 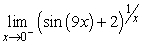
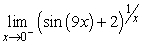

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
22
Let y = x3 - 6. Find y if x = 3 and the initial value of x is x = 2.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
23
Answer true or false. A circular spill is spreading so that when its radius r is 1 m, dr = 0.005 m. The corresponding change in the area covered by the spill, A, is, to the nearest hundredth of a square meter, 0.008 m2.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
24
Answer true or false. A cube is expanding as temperature increases. If the length of the cube is changing at a rate of dx = 0.6 mm when x is 3.5 m, the volume is experiencing a corresponding change of 22,050,000 mm3.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
25
A small suspended droplet of radius 10 microns is growing. If dr = 0.004 micron find the change in the volume, dV, to the nearest thousandth of a cubic micron.
A) 1.257 cubic microns
B) 1.676 cubic microns
C) 1.600 cubic microns
D) 5.027 cubic microns
E) 1256.637 cubic microns
A) 1.257 cubic microns
B) 1.676 cubic microns
C) 1.600 cubic microns
D) 5.027 cubic microns
E) 1256.637 cubic microns

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate. 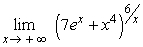
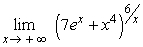

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
27
y = x8. Find the formula for dy.
A) dy = 8x7
B) dy = 8(x + dx)7
C) dy = 8x7 - 8(dx)7
D) dy = (x + dx)8 - x8
E) dy = 8x7dx
A) dy = 8x7
B) dy = 8(x + dx)7
C) dy = 8x7 - 8(dx)7
D) dy = (x + dx)8 - x8
E) dy = 8x7dx

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
28
If y = x4, find the formula for y.
A)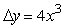
B)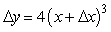
C)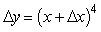
D)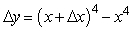
E)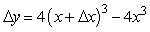
A)
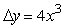
B)
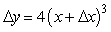
C)
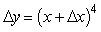
D)
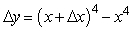
E)
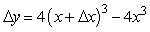

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
29
y = cos x. Find the formula for dy.
A) dy = -sin (x + dx)
B) dy = -sin (x + dx) - sin x dx
C) dy = -sin x dx
D) dy = -sin (x + dx) + sin x dx
E) dy = -sin (x + dx) - sin dx
A) dy = -sin (x + dx)
B) dy = -sin (x + dx) - sin x dx
C) dy = -sin x dx
D) dy = -sin (x + dx) + sin x dx
E) dy = -sin (x + dx) - sin dx

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
30
Let 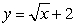 . Find y at x = 4 if x = 1.1.
. Find y at x = 4 if x = 1.1.
A) 1.100
B) 0.275
C) 0.250
D) 0.550
E) 0
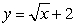 . Find y at x = 4 if x = 1.1.
. Find y at x = 4 if x = 1.1.A) 1.100
B) 0.275
C) 0.250
D) 0.550
E) 0

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
31
Let 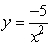 . Find dy at x = 3 if dx = 0.032.
. Find dy at x = 3 if dx = 0.032.
A) -0.0118
B) 0.1066
C) 0.0118
D) 0.3703
E) -0.0177
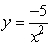 . Find dy at x = 3 if dx = 0.032.
. Find dy at x = 3 if dx = 0.032.A) -0.0118
B) 0.1066
C) 0.0118
D) 0.3703
E) -0.0177

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
32
If 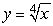 , find the formula for y.
, find the formula for y.
A)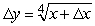
B)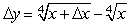
C)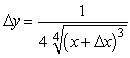
D)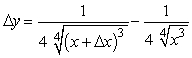
E)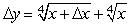
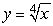 , find the formula for y.
, find the formula for y.A)
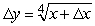
B)
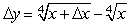
C)
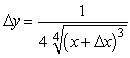
D)
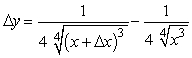
E)
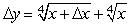

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
33
Use dy to approximate 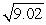 starting at x = 9.
starting at x = 9.
A) 3.003
B) 9.003
C) 2.997
D) 3.001
E) 3.167
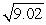 starting at x = 9.
starting at x = 9.A) 3.003
B) 9.003
C) 2.997
D) 3.001
E) 3.167

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
34
y = sin x cos x. Find the formula for dy.
A) dy = -sin x cos x dx
B) dy = (-sin 2x + cos 2x) dx
C) dy = -sin 2(x + dx) + cos 2(x + dx)
D) dy = (-sin 2(x + dx) + cos 2(x + dx)) - (-sin 2 x + cos 2x)
E) dy = sin (x +dx) cos (x +dx) - sin x cos x
A) dy = -sin x cos x dx
B) dy = (-sin 2x + cos 2x) dx
C) dy = -sin 2(x + dx) + cos 2(x + dx)
D) dy = (-sin 2(x + dx) + cos 2(x + dx)) - (-sin 2 x + cos 2x)
E) dy = sin (x +dx) cos (x +dx) - sin x cos x

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
35
If y = tan x, find the formula for y.
A)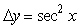
B)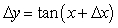
C)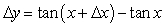
D)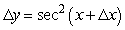
E)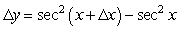
A)
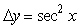
B)
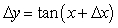
C)
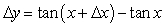
D)
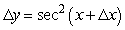
E)
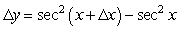

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
36
Let y = 4x4. Find dy at x = 4 if dx = -0.01.
A) 1024
B) -40.96
C) -163.84
D) -102,400
E) -10.24
A) 1024
B) -40.96
C) -163.84
D) -102,400
E) -10.24

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
37
A particle moves according to s = t3. Find ds if t = 5 and dt = 4.
A) 75
B) 100
C) 300
D) 500
E) 60
A) 75
B) 100
C) 300
D) 500
E) 60

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
38
Let y = x3 - 3. Find dy if dx = 1 and the initial value of x is x = 3.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
39
Approximate sin 30.075°.
A) 0.4993
B) 0.5003
C) 0.5013
D) 0.5023
E) 0.5033
A) 0.4993
B) 0.5003
C) 0.5013
D) 0.5023
E) 0.5033

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
40
Answer true or false. The formula for dy is D y = f(x)dx.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
41
Use a differential to approximate 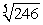 .
.
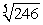 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
42
A circular hole 6 inches in diameter and 12 feet deep is to be drilled out of a glacier. The diameter of the hole is exact but the depth of the hole is measured with an error of ±1%. Estimate the percentage error in the volume of ice removed. ( 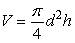 is the volume of a cylinder of diameter d and height h.)
is the volume of a cylinder of diameter d and height h.)
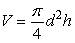 is the volume of a cylinder of diameter d and height h.)
is the volume of a cylinder of diameter d and height h.)
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
43
Use a differential to approximate cos 65°.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
44
Use a differential to approximate sin 36°.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
45
Let y = x4 and dx = 0.05 at x = 4. Find dy.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
46
When a cubical block of metal is heated, each edge increases by 0.1% per degree increase in temperature. Use differentials to estimate the percentage increase in the surface area and volume of the block per degree increase in temperature.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
47
Use a differential to approximate tan 41°.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
48
Let 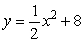 . Find y if x = 1 and the initial value of x is x = 1.
. Find y if x = 1 and the initial value of x is x = 1.
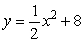 . Find y if x = 1 and the initial value of x is x = 1.
. Find y if x = 1 and the initial value of x is x = 1. 
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
49
The surface area of a sphere is given by S = 4 r2 where r is the radius of the sphere. The radius is measured to be 6cm with an error of ±0.07cm. Use differentials to estimate the error in the calculated surface area.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
50
When a spherical ball of metal is heated, the radius of the sphere increases by 0.3% per degree increase in temperature. Use differentials to estimate the percentage increase in the surface area and volume of the ball per degree increase in temperature. 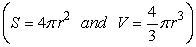
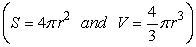

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
51
The area of a circle is to be computed from a measured value of its diameter. Estimate the maximum permissible percentage error in the measurement if the percentage error in the area must be kept within 0.5%.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
52
Use a differential to approximate 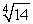 .
.
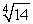 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
53
Let 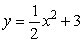 . Find dy if dx = 2 and the initial value of x is x = 2.
. Find dy if dx = 2 and the initial value of x is x = 2.
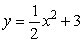 . Find dy if dx = 2 and the initial value of x is x = 2.
. Find dy if dx = 2 and the initial value of x is x = 2.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
54
The surface area S of a cube is to be computed from a measured value of its side x. Estimate the maximum permissible percentage error in the side measurement if the percentage error in the surface area must be kept to within ±1%.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
55
Let y = 2x2 and dx = 0.04 at x = 4. Find dy.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
56
The magnetic force F acting on a particle is given by 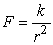 , where r is the distance from the magnetic source and k is a constant. r is measured to be 4cm with a possible error of ±3%. Use differentials to estimate the error in the calculated value of F.
, where r is the distance from the magnetic source and k is a constant. r is measured to be 4cm with a possible error of ±3%. Use differentials to estimate the error in the calculated value of F.
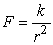 , where r is the distance from the magnetic source and k is a constant. r is measured to be 4cm with a possible error of ±3%. Use differentials to estimate the error in the calculated value of F.
, where r is the distance from the magnetic source and k is a constant. r is measured to be 4cm with a possible error of ±3%. Use differentials to estimate the error in the calculated value of F.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
57
The magnetic force F acting on a particle is given by 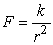 , where r is the distance from the magnetic source and k is a constant. r is measured to be 2cm with a possible error of ±8%. Estimate the percentage error in F and r.
, where r is the distance from the magnetic source and k is a constant. r is measured to be 2cm with a possible error of ±8%. Estimate the percentage error in F and r.
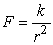 , where r is the distance from the magnetic source and k is a constant. r is measured to be 2cm with a possible error of ±8%. Estimate the percentage error in F and r.
, where r is the distance from the magnetic source and k is a constant. r is measured to be 2cm with a possible error of ±8%. Estimate the percentage error in F and r.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
58
Find the formula for dy if y = x6.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
59
The pressure P, the volume V, and the temperature T of an enclosed gas are related by the Ideal Gas Law, PV = kT where k is a constant. With the temperature held constant, the volume of the gas is calculated from a measured value of its pressure. Estimate the maximum permissible error in the pressure measurement if the percentage error in the volume must be kept to within ±3%.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
60
Use a differential to approximate (2.97)5.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
61
Answer true or false. Suppose z = 3yx. Then dz/dt = 3x(dy/dt)+3y(dx/dt).

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
62
The power in watts for a circuit is given by P = I 2R. How fast is the power changing if the resistance, R, of the circuit is 1,400 , the current, I, is 1.5A, and the current is decreasing with respect to time at a rate of 0.025 A/s. (Assume R is a constant.)
A) 105 w/s
B) 4,200 w/s
C) 26.25 w/s
D) 157.5 w/s
E) -105 w/s
A) 105 w/s
B) 4,200 w/s
C) 26.25 w/s
D) 157.5 w/s
E) -105 w/s

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
63
Answer true or false. If z = 2x3y2, then 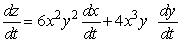 .
.
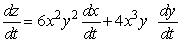 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
64
The number of board feet of lumber in a log that is 10 feet long is given by the formula 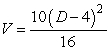 , where D is the diameter of the tree in inches. In a tree that will produce a 10 foot log and has a current diameter of 22 inches, the diameter is changing at a rate of 3.45 inches per year. How fast is the volume increasing?
, where D is the diameter of the tree in inches. In a tree that will produce a 10 foot log and has a current diameter of 22 inches, the diameter is changing at a rate of 3.45 inches per year. How fast is the volume increasing?
A) 22.5 ft3/year
B) 38.8125 ft3/year
C) 77.625 ft3/year
D) 11.3 ft3/year
E) 202.5 ft3/year
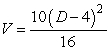 , where D is the diameter of the tree in inches. In a tree that will produce a 10 foot log and has a current diameter of 22 inches, the diameter is changing at a rate of 3.45 inches per year. How fast is the volume increasing?
, where D is the diameter of the tree in inches. In a tree that will produce a 10 foot log and has a current diameter of 22 inches, the diameter is changing at a rate of 3.45 inches per year. How fast is the volume increasing?A) 22.5 ft3/year
B) 38.8125 ft3/year
C) 77.625 ft3/year
D) 11.3 ft3/year
E) 202.5 ft3/year

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
65
Answer true or false. If A = 3 r3, then 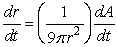 .
.
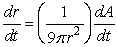 .
. 
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
66
Answer true or false. Suppose z = 4yx. Then dz/dt = 4(dy/dt)(dx/dt).

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
67
The volume of a cylinder is given by V = r2h. Find 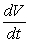 in terms of
in terms of 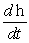 . (Assume that r is a constant.)
. (Assume that r is a constant.)
A)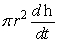
B) 1
C)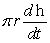
D)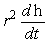
E)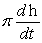
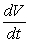 in terms of
in terms of 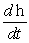 . (Assume that r is a constant.)
. (Assume that r is a constant.)A)
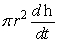
B) 1
C)
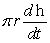
D)
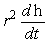
E)
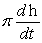

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
68
Find the formula for dy if 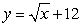 .
.
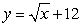 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
69
Answer true or false. If sin = 8xy, then 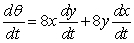 .
.
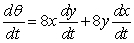 .
. 
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
70
Answer true or false. Water is running out of an inverted conical tank so the height is changing at a rate of 4 ft/s. The height of the water in the tank is changing at 4 ft/s if the height is currently 10 ft and the radius is 8 ft.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
71
Gravitational force is inversely proportional to the distance between two objects squared. If F = 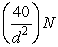 at a distance d = 2m, how fast is the force diminishing if the objects are moving away from each other at 0.1 m/s?
at a distance d = 2m, how fast is the force diminishing if the objects are moving away from each other at 0.1 m/s?
A) 1 N/s
B) -1 N/s
C) -10 N/s
D) 10 N/s
E) 0 N/s
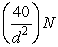 at a distance d = 2m, how fast is the force diminishing if the objects are moving away from each other at 0.1 m/s?
at a distance d = 2m, how fast is the force diminishing if the objects are moving away from each other at 0.1 m/s?A) 1 N/s
B) -1 N/s
C) -10 N/s
D) 10 N/s
E) 0 N/s

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
72
Find the formula for y if y = csc x.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
73
Answer true or false. If A = 8xy, then 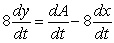
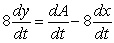

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
74
A point P is moving along a curve whose equation is 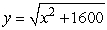 . When P = (9, 41) , y is increasing at a rate of 2 units/s. How fast is x changing?
. When P = (9, 41) , y is increasing at a rate of 2 units/s. How fast is x changing?
A) 0.439 units/s
B) 738 units/s
C) 8.111 units/s
D) 9.111 units/s
E) 10.111 units/s
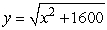 . When P = (9, 41) , y is increasing at a rate of 2 units/s. How fast is x changing?
. When P = (9, 41) , y is increasing at a rate of 2 units/s. How fast is x changing?A) 0.439 units/s
B) 738 units/s
C) 8.111 units/s
D) 9.111 units/s
E) 10.111 units/s

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
75
Find the formula for y if y = 3x4 - 9.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
76
Answer true or false. A cube is expanding, so 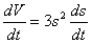 .
.
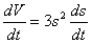 .
.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
77
Find the formula for dy if y = cot x.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
78
Suppose z = x2 + y5. Then dz/dt =
A)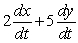
B)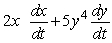
C)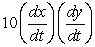
D)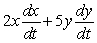
E)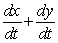
A)
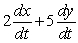
B)
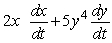
C)
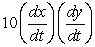
D)
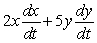
E)
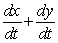

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
79
Answer true or false. A plane is approaching an observer with a horizontal speed of 140ft/s and is currently 7,000ft from being directly overhead at an altitude of 12,000ft. The rate at which the angle of elevation, , is changing with respect to time, d /dt = (1/x)dy/dt. Where x is the horizontal distance and y is the altitude.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
80
A 10-ft ladder rests against a wall at /4 radians. If it were to begin to slip, when the bottom of the ladder is moving at 0.08 ft/s, how fast would the top of the ladder be moving down the wall? (How fast would the height of the upper end of the ladder on the side of the wall be changing?)
A) 0.074 ft/s
B) 0.071 ft/s
C) 0.069 ft/s
D) 0.080 ft/s
E) 0.088 ft/s
A) 0.074 ft/s
B) 0.071 ft/s
C) 0.069 ft/s
D) 0.080 ft/s
E) 0.088 ft/s

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck


