Deck 12: Vector-Valued Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/147
Play
Full screen (f)
Deck 12: Vector-Valued Functions
1
r(t) = 4t3 i + (17 + 2t)j is the position vector of a particle moving in a plane. Find the acceleration.
A) 12t2 i + 2j
B) 12i
C) 24t i + 2j
D) 24t i
E) 24i
A) 12t2 i + 2j
B) 12i
C) 24t i + 2j
D) 24t i
E) 24i
24t i
2
An object in orbit has rmin = 1024km and e = 0.49. Find rmax.
A) 2.92 *1026km
B) 3.21 * 1026km
C) 3.21 * 1025km
D) 2.92 * 1024km
E) 2.92 *1025km
A) 2.92 *1026km
B) 3.21 * 1026km
C) 3.21 * 1025km
D) 2.92 * 1024km
E) 2.92 *1025km
2.92 * 1024km
3
If, for an elliptical orbit, rmin = 1025km and e = 0.55, find a, the semimajor axis.
A) 2.44*1025km
B) 2.22 * 1025km
C) 2.44 * 1024km
D) 2.22 * 1024km
E) 1.72 *1025km
A) 2.44*1025km
B) 2.22 * 1025km
C) 2.44 * 1024km
D) 2.22 * 1024km
E) 1.72 *1025km
2.22 * 1025km
4
The position vector of a particle moving in a plane is given by 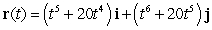 . Find the velocity.
. Find the velocity.
A)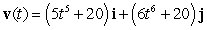
B)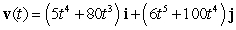
C)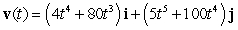
D)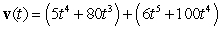
E)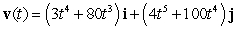
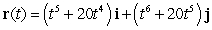 . Find the velocity.
. Find the velocity.A)
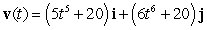
B)
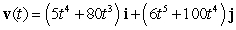
C)
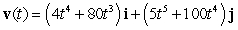
D)
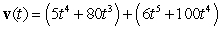
E)
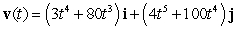

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
5
The velocity vector of a particle moving in a plane is given by 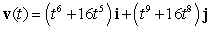 . Find the acceleration vector.
. Find the acceleration vector.
A)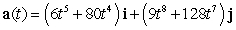
B)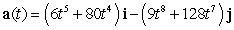
C)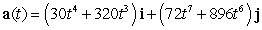
D)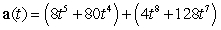
E)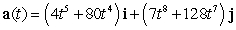
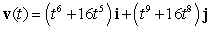 . Find the acceleration vector.
. Find the acceleration vector.A)
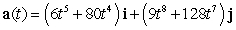
B)
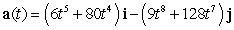
C)
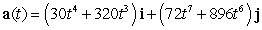
D)
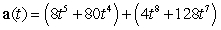
E)
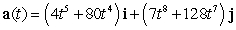

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
6
An object in an elliptical orbit has 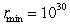 and
and 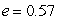 Find rmax.
Find rmax.
A)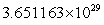 km
km
B)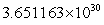 km
km
C)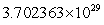 km
km
D)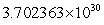 km
km
E)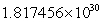 km
km
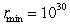 and
and 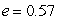 Find rmax.
Find rmax.A)
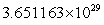 km
kmB)
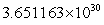 km
kmC)
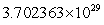 km
kmD)
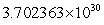 km
kmE)
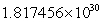 km
km
Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
7
If an asteroid has an orbit with eccentricity 0.59 and semi-major axis a = 130000000, find its minimum distance from the center of the sun.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
8
If, for an elliptical orbit, rmax = 1025km and e = 0.51, find a, the semimajor axis.
A) 3.25*1024km
B) 6.62 *1025km
C) 6.62 *1024km
D) 5.96 * 1024km
E) 7.28 * 1024km
A) 3.25*1024km
B) 6.62 *1025km
C) 6.62 *1024km
D) 5.96 * 1024km
E) 7.28 * 1024km

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
9
A 2.03* 1030-kg object is orbited by an object 1.42 *1015 m above its center. If the orbit is circular, find its velocity. G = 6.67 * 10-11 m3/kg·s2.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
10
The position vector of a particle moving in a plane is given by 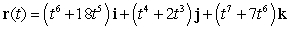 . Find the velocity.
. Find the velocity.
A)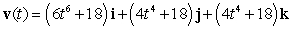
B)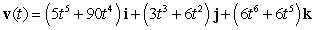
C)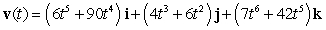
D)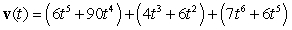
E)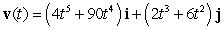
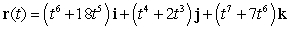 . Find the velocity.
. Find the velocity.A)
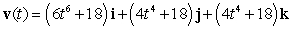
B)
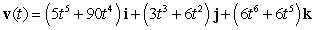
C)
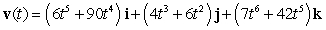
D)
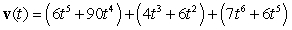
E)
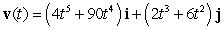

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
11
Find the speed of a particle in a circular orbit with radius 1021m around an object of mass 1018kg. (G = 6.67 *10-11m/kg·s2)
A) 1.50 * 1013m/s
B) 6.67*10-14m/s
C) 3.87 * 106m/s
D) 2.58 * 10-7m/s
E) 4.91 *10-7m/s
A) 1.50 * 1013m/s
B) 6.67*10-14m/s
C) 3.87 * 106m/s
D) 2.58 * 10-7m/s
E) 4.91 *10-7m/s

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
12
If, for an elliptical orbit, rmin = 1025km and e = 0.86, find a, the semimajor axis.
A) 7.14 * 1024km
B) 7.14 *1025km
C) 13.29 * 1025km
D) 13.29 * 1024km
E) 3.64 *1025km
A) 7.14 * 1024km
B) 7.14 *1025km
C) 13.29 * 1025km
D) 13.29 * 1024km
E) 3.64 *1025km

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
13
Find the speed of a particle in a circular orbit with radius 1022m around an object of mass 1023kg. (G = 6.67 *10-11m/kg·s2)
A) 1.50 *109 m/s
B) 6.67 * 10-10 m/s
C) 3.87 * 104 m/s
D) 2.58 *10-5 m/s
E) 4.91*10-5m/s
A) 1.50 *109 m/s
B) 6.67 * 10-10 m/s
C) 3.87 * 104 m/s
D) 2.58 *10-5 m/s
E) 4.91*10-5m/s

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
14
An object in an elliptical orbit has 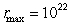 and
and 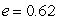 Find rmin.
Find rmin.
A)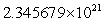 km
km
B)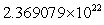 km
km
C)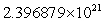 km
km
D)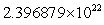 km
km
E)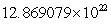 km
km
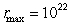 and
and 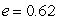 Find rmin.
Find rmin.A)
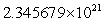 km
kmB)
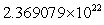 km
kmC)
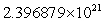 km
kmD)
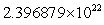 km
kmE)
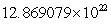 km
km
Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
15
Given G = 6.67 * 10-11 m3/kg·s2, find the radius of a circular orbit above a 1050-kg mass, if the orbiting object has a speed of 51 m/s.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
16
If, for an elliptical orbit, rmax = 1025km and e = 0.79, find a, the semi-major axis.
A) 1.17 *1025km
B) 4.76 *1025km
C) 5.59 * 1025km
D) 5.59 * 1024km
E) 1.17 * 1024km
A) 1.17 *1025km
B) 4.76 *1025km
C) 5.59 * 1025km
D) 5.59 * 1024km
E) 1.17 * 1024km

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
17
If an asteroid has an orbit with eccentricity 0.59 and semi-major axis a = 130000000, find its maximum distance from the center of the sun.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
18
If an object orbits the sun with rmax = 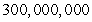 miles and rmin =
miles and rmin = 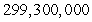 miles, the elliptical orbit has eccentricity
miles, the elliptical orbit has eccentricity
A)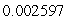
B)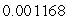
C) 40
D)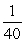
E) 1
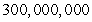 miles and rmin =
miles and rmin = 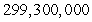 miles, the elliptical orbit has eccentricity
miles, the elliptical orbit has eccentricityA)
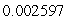
B)
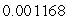
C) 40
D)
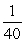
E) 1

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
19
If, for an elliptical orbit with semimajor axis a, rmin = a(1 - e) and rmax = a(1 + e), find the eccentricity if rmax = 1,100,000,000 km and rmin = 910,000,000 km.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
20
An object in orbit has rmax = 1024km and e = 0.27. Find rmin.
A) 5.75 * 1023km
B) 6.32 *1023km
C) 5.46 *1023km
D) 5.75 *1026km
E) 6.32 * 1026km
A) 5.75 * 1023km
B) 6.32 *1023km
C) 5.46 *1023km
D) 5.75 *1026km
E) 6.32 * 1026km

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
21
Find the velocity, speed, and acceleration of a particle whose position is given by r(t) = e t i + e2t j at t = 0 seconds, then sketch the path of the particle together with the velocity and acceleration vectors at t = 0 seconds.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
22
r(t) = t3 i - 2t j; 1 t 5. Find the displacement.
A) 124i - 8j
B) 125i - 8j
C) 124i + 10j
D) 124i + 8j
E) -124i - 8j
A) 124i - 8j
B) 125i - 8j
C) 124i + 10j
D) 124i + 8j
E) -124i - 8j

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
23
Find the speed of a particle moving along the curve r(t) = (13 + t3)i + 4t j - t2 k at t = 1.
A)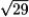
B)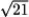
C)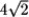
D)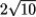
E)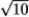
A)
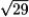
B)
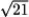
C)
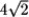
D)
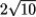
E)
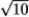

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
24
If 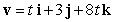 , find
, find 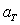 .
.
A)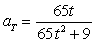
B)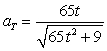
C)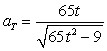
D)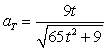
E)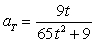
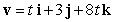 , find
, find 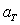 .
.A)
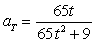
B)
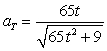
C)
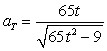
D)
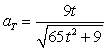
E)
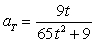

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
25
Find the velocity, speed, and acceleration of a particle whose position is given by r(t) = 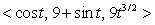 at
at 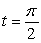 seconds.
seconds.
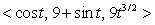 at
at 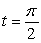 seconds.
seconds.
Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
26
A particle travels along a curve given by r(t) = 7 cos 3t i - 7 sin 3t j + 2k. Find the distance traveled by the particle during the time interval 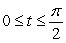 seconds.
seconds.
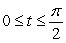 seconds.
seconds.
Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
27
r(t) = 3t i + 6t j + 7t k is the position vector of a particle moving in a plane. Find the acceleration of the particle.
A) 3i + 6j + 9k
B) 18
C) 0
D) i + j + k
E) 3i - 6j - 9k
A) 3i + 6j + 9k
B) 18
C) 0
D) i + j + k
E) 3i - 6j - 9k

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
28
r(t) = 31t + t3 i - 2t2 j is the position vector of a particle moving in a plane. Find the acceleration at an arbitrary time t.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
29
r(t) = (-1 + t3)i - 2t j; 1 t 2. Find the distance.
A)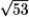
B)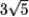
C)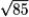
D) 9
E) 81
A)
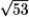
B)
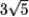
C)
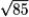
D) 9
E) 81

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
30
If v = 2i and a = 5i - 7j, find aT .
A) 5
B) 6
C)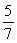
D) 8
E) 9
A) 5
B) 6
C)
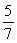
D) 8
E) 9

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
31
A shell is fired from a mortar at ground level with a velocity of 200 meters per second at an elevation of 60°. How far does the shell travel horizontally?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
32
r(t) = 4t3 i + (2t + 3)j is the position vector of a particle moving in a plane. Find the speed at t = 1.
A)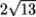
B) 12
C) 24
D) 0
E)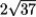
A)
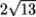
B) 12
C) 24
D) 0
E)
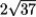

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
33
Find the velocity, speed, and acceleration of a particle whose position is given by r(t) = 10 + e t i + e t cos t j + e t sin t k at t = 0 seconds.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
34
If v = 2i and a = 7i - 9j, find aN .
A) 16
B) -16
C)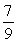
D) 9
E) -9
A) 16
B) -16
C)
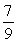
D) 9
E) -9

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
35
Find the velocity of a particle moving along the curve r(t) = (-8 + t3)i + 4t j - t2 k at t = 1.
A) 3i + 4j - 2k
B) 6i - 2j
C) 3i + 4j + 2k
D) 0
E) 3i - 4j - 2k
A) 3i + 4j - 2k
B) 6i - 2j
C) 3i + 4j + 2k
D) 0
E) 3i - 4j - 2k

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
36
A particle moves through 3-space in such a way that its velocity is 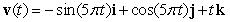 . Find the coordinates of the particle at t = 1 second if the particle was initially at
. Find the coordinates of the particle at t = 1 second if the particle was initially at 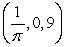 at t = 0 seconds.
at t = 0 seconds.
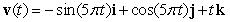 . Find the coordinates of the particle at t = 1 second if the particle was initially at
. Find the coordinates of the particle at t = 1 second if the particle was initially at 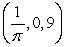 at t = 0 seconds.
at t = 0 seconds.
Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
37
If 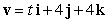 , find
, find 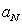 when t = 1.
when t = 1.
A)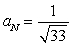
B)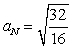
C)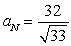
D)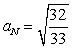
E)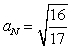
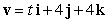 , find
, find 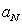 when t = 1.
when t = 1.A)
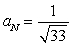
B)
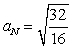
C)
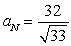
D)
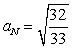
E)
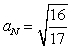

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
38
Find the acceleration of a particle moving along the curve r(t) = t3 i + (8 + 4t)j - t2 k at t = 1.
A) 3i + 4j - 2k
B) 6i - 2k
C) 3i + 4j + 2k
D) 0
E) 3i - 4j - 2k
A) 3i + 4j - 2k
B) 6i - 2k
C) 3i + 4j + 2k
D) 0
E) 3i - 4j - 2k

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
39
Find the velocity, speed, and acceleration of a particle whose position is given by r(t) = 4 cos t, sin t at 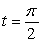 seconds, then sketch the path of the particle together with the velocity and acceleration vectors at
seconds, then sketch the path of the particle together with the velocity and acceleration vectors at 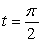 seconds.
seconds.
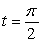 seconds, then sketch the path of the particle together with the velocity and acceleration vectors at
seconds, then sketch the path of the particle together with the velocity and acceleration vectors at 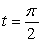 seconds.
seconds. 
Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
40
A particle travels along a curve given by r(t) = e t cos t i + e t sin t j + 12k. Find the distance traveled by the particle during the time interval 0 t seconds.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
41
Find the radius of curvature for x = t2 + 4, y = t - 2, at t = 2.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
42
Find the curvature 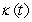 for r(t) = 17i + 2t j + 3t2 k at t = 0.
for r(t) = 17i + 2t j + 3t2 k at t = 0.
A)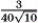
B)
C) 0
D) 1
E)
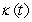 for r(t) = 17i + 2t j + 3t2 k at t = 0.
for r(t) = 17i + 2t j + 3t2 k at t = 0.A)
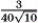
B)

C) 0
D) 1
E)


Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
43
If 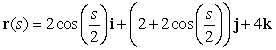 , find k(s).
, find k(s).
A)
B)
C) 2
D) 4
E) 0
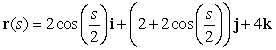 , find k(s).
, find k(s).A)

B)

C) 2
D) 4
E) 0

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
44
At what points does 4x2 + 25y2 = 100 have minimum curvature?
A) (0, -4), (0, 4)
B) (-4, 0), (4, 0)
C) (-5, 0), (5, 0)
D) (0, -5), (0, 5)
E) (0, -2), (0, 2)
A) (0, -4), (0, 4)
B) (-4, 0), (4, 0)
C) (-5, 0), (5, 0)
D) (0, -5), (0, 5)
E) (0, -2), (0, 2)

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
45
At what point does 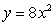 have maximum curvature?
have maximum curvature?
A) (0, -4)
B) (-1, 0)
C) (-5, 0)
D) (0, 0)
E) (0, 1)
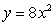 have maximum curvature?
have maximum curvature?A) (0, -4)
B) (-1, 0)
C) (-5, 0)
D) (0, 0)
E) (0, 1)

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
46
Find the curvature 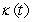 for
for 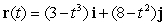 .
.
A)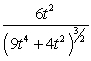
B)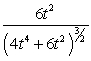
C)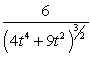
D) 6
E)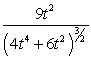
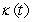 for
for 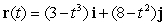 .
.A)
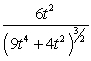
B)
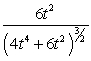
C)
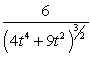
D) 6
E)
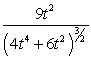

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
47
If x = t3, y = 12 + t2, then k(t) at t = 1 is
A)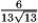
B)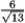
C) 0
D)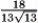
E)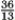
A)
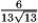
B)
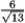
C) 0
D)
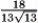
E)
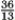

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
48
If y = cos x, find the curvature at 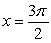 .
.
A) 0
B) 1
C) -1
D)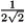
E)
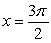 .
.A) 0
B) 1
C) -1
D)
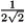
E)


Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
49
Find the curvature 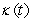 for r(t) = (16 + sin t) i + (16 + cos t) j.
for r(t) = (16 + sin t) i + (16 + cos t) j.
A) 1
B) -1
C) 0
D) sin2t - cos2t
E) - sin2t + cos2t
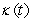 for r(t) = (16 + sin t) i + (16 + cos t) j.
for r(t) = (16 + sin t) i + (16 + cos t) j.A) 1
B) -1
C) 0
D) sin2t - cos2t
E) - sin2t + cos2t

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
50
If r(t) = (2t2 - 5)i + (t - 2)j + (4t + 10)k, find the curvature k(t) at t = 1.
A)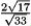
B)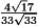
C)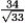
D)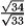
E)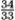
A)
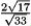
B)
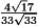
C)
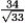
D)
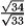
E)
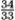

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
51
Find the radius of curvature for r(t) = 4 sin t, 2t - sin 2t - 3, cos 2t at 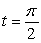 .
.
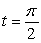 .
. 
Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
52
Find the curvature for x = -11 + t3, y = 2t2 at t = 1.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
53
Find the curvature 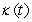 for r(t) = e t i + e t j + 30k.
for r(t) = e t i + e t j + 30k.
A) 0
B)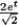
C)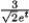
D)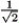
E) 2e
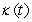 for r(t) = e t i + e t j + 30k.
for r(t) = e t i + e t j + 30k.A) 0
B)
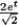
C)
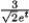
D)
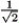
E) 2e

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
54
Find the curvature for x = 2e t , y = 11 + 2e-t at t = 0.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
55
Find the curvature 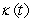 for
for 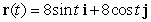
A) 1
B)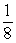
C) 0
D) sin2t - cos2t
E) - sin2t + cos2t
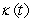 for
for 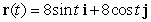
A) 1
B)
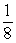
C) 0
D) sin2t - cos2t
E) - sin2t + cos2t

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
56
If 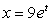 and
and 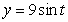 , then k(t) at t = 0 is
, then k(t) at t = 0 is
A)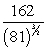
B)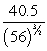
C)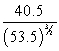
D)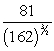
E)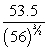
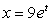 and
and 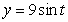 , then k(t) at t = 0 is
, then k(t) at t = 0 isA)
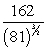
B)
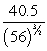
C)
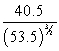
D)
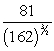
E)
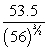

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
57
Find the curvature 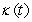 for
for 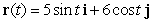
A)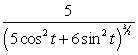
B)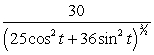
C)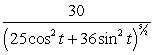
D)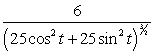
E)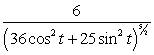
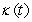 for
for 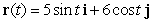
A)
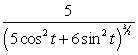
B)
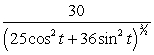
C)
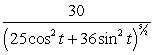
D)
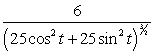
E)
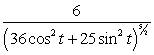

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
58
Find the curvature for r(t) = 6 cos 2t + 19, 6 sin 2t, 5t at t = .

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
59
If 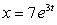 and
and 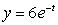 , then k(t) at t = 0 is
, then k(t) at t = 0 is
A)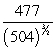
B)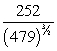
C)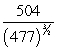
D)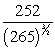
E)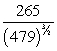
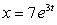 and
and 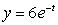 , then k(t) at t = 0 is
, then k(t) at t = 0 isA)
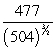
B)
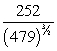
C)
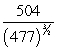
D)
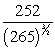
E)
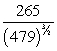

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
60
Find the curvature 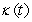 for r(t) = cos t i + sin t j - 10k.
for r(t) = cos t i + sin t j - 10k.
A)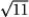
B) 1
C) sin2t - cos2t
D) sin2t + cos2t
E) - sin2t + cos2t
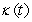 for r(t) = cos t i + sin t j - 10k.
for r(t) = cos t i + sin t j - 10k.A)
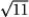
B) 1
C) sin2t - cos2t
D) sin2t + cos2t
E) - sin2t + cos2t

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
61
Let r(t) = 2t i + (10 + 3t)j. Find T(t).
A)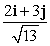
B)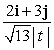
C) 2i + 3j
D)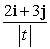
E)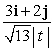
A)
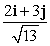
B)
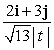
C) 2i + 3j
D)
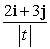
E)
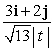

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
62
Let r(t) = e t i + e2t j + (e3t + 3)k. Find T(t) when t = 0.
A)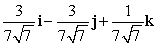
B) 6i - 6j + 2k
C)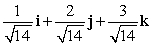
D)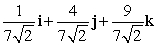
E) i
A)
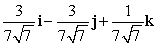
B) 6i - 6j + 2k
C)
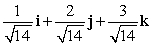
D)
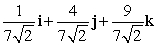
E) i

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
63
Find the curvature for x = e t , y = 3 + e t cos t, z = e t sin t at t = 0.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
64
Sketch x = 2 cos t, y = 3 sin t for 0 t 2 . Calculate the radius of curvature at 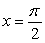 and sketch the oscillating circle.
and sketch the oscillating circle.
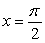 and sketch the oscillating circle.
and sketch the oscillating circle. 
Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
65
Let r(t) = (t2 + 2)i + (10 + e t )j + e t k. Find B(t) for t = 0. Approximate your calculations to three decimal places.
A) 2i + 0.707j + 0.707k
B) 0.707j - 0.707k
C) 2i + 0.577j + 0.577k
D) 0.577j - 0.577k
E) 1.732i - 1.732j - 1.732k
A) 2i + 0.707j + 0.707k
B) 0.707j - 0.707k
C) 2i + 0.577j + 0.577k
D) 0.577j - 0.577k
E) 1.732i - 1.732j - 1.732k

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
66
Find the curvature for x2 + y2 = 10x + 10 at (2, -4).

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
67
Let r(t) = (t3 + 2)i + te t j + (9 + e t )k. Find T(t) for t = 0.
A)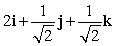
B)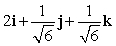
C)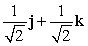
D)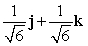
E)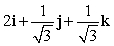
A)
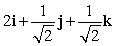
B)
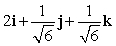
C)
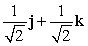
D)
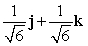
E)
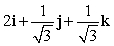

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
68
Let r(t) = (t2 + 9)i + e t j + e t k. Find N(t) for t = 0. Approximate your calculations to three decimal places.
A) 0
B) i
C) 0.577j - 0.577k
D) i + 0.577j + 0.577k
E) 1.732i - 1.732j - 1.732k
A) 0
B) i
C) 0.577j - 0.577k
D) i + 0.577j + 0.577k
E) 1.732i - 1.732j - 1.732k

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
69
Let r(t) = (t2 + 2)i + e t j + (12 + e t )k. Find N(t) for t = 0.
A)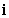
B)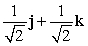
C)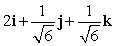
D)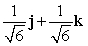
E)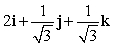
A)
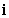
B)
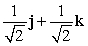
C)
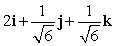
D)
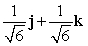
E)
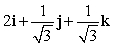

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
70
Find the curvature for 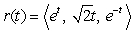 at t = 0.
at t = 0.
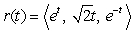 at t = 0.
at t = 0.
Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
71
Let r(t) = 4 i + (t + 2) j + 4 k. Find T(t) for t = 0.
A)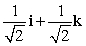
B)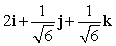
C)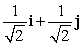
D)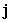
E)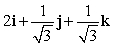
A)
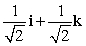
B)
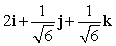
C)
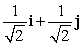
D)
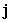
E)

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
72
Let r(t) = (-9 + t) i + t2 j + t3 k. Find T(t) when t = 0.
A) i
B)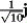
C)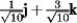
D)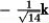
E)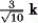
A) i
B)
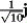
C)
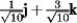
D)
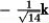
E)

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
73
Let r(t) = (t2 + 2)i + (e t + 4)j + e t k. Find N(t) for t = 0. Approximate your calculations to three decimal places.
A) 0
B) i
C) 0.577j + 0.577k
D) i + 0.577j + 0.577k
E) i - 1.732j - 1.732k
A) 0
B) i
C) 0.577j + 0.577k
D) i + 0.577j + 0.577k
E) i - 1.732j - 1.732k

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
74
Let r(t) = 3t2 i + (4 + 4t2)j + 6t k. Find B(t).
A)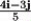
B) 0
C)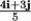
D)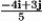
E) i + j + k
A)
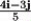
B) 0
C)
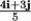
D)
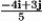
E) i + j + k

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
75
Sketch 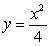 . Calculate the radius of curvature at x = 1 and sketch the oscillating circle.
. Calculate the radius of curvature at x = 1 and sketch the oscillating circle.
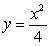 . Calculate the radius of curvature at x = 1 and sketch the oscillating circle.
. Calculate the radius of curvature at x = 1 and sketch the oscillating circle.
Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
76
Let r(t) = (t3 + 2)i + te t j + (7 + e t )k. Find N(t) for t = 0.
A)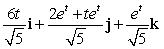
B)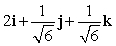
C)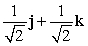
D)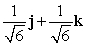
E)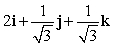
A)
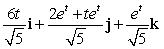
B)
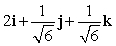
C)
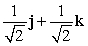
D)
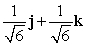
E)
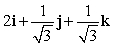

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
77
Let r(t) = (t2 + 2)i + e t j + (9 + e t )k. Find T(t) for t = 0.
A)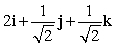
B)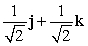
C)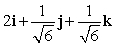
D)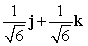
E)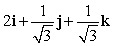
A)
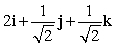
B)
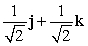
C)
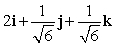
D)
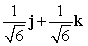
E)
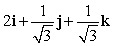

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
78
Let r(t) = (t + 2)i + e t j + 12 k. Find T(t) for t = 0.
A)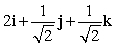
B)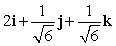
C)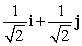
D)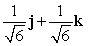
E)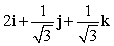
A)
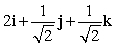
B)
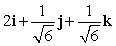
C)
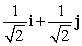
D)
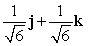
E)
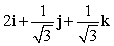

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
79
Let r(t) = e t i + (t + 2) j + 10 k. Find T(t) for t = 0.
A)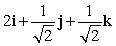
B)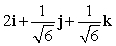
C)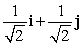
D)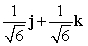
E)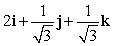
A)
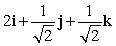
B)
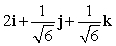
C)
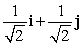
D)
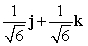
E)
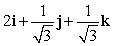

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
80
Let r(t) = (t2 + 2)i + e t j + ( 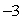 + e t )k. Find B(t) for t = 0. Approximate your calculations to three decimal places.
+ e t )k. Find B(t) for t = 0. Approximate your calculations to three decimal places.
A) 2i + 0.707j + 0.707k
B) 0.707j - 0.707k
C) 2i + 0.577j + 0.577k
D) 0.577j - 0.577k
E) 1.334i - 1.334j - 1.334k
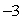 + e t )k. Find B(t) for t = 0. Approximate your calculations to three decimal places.
+ e t )k. Find B(t) for t = 0. Approximate your calculations to three decimal places.A) 2i + 0.707j + 0.707k
B) 0.707j - 0.707k
C) 2i + 0.577j + 0.577k
D) 0.577j - 0.577k
E) 1.334i - 1.334j - 1.334k

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck


