Deck 1: Limits and Continuity
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/186
Play
Full screen (f)
Deck 1: Limits and Continuity
1
Find the limit. 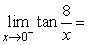
A) 0
B) -1
C) 1
D)
E) Does not exist
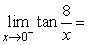
A) 0
B) -1
C) 1
D)
E) Does not exist
Does not exist
2
Find 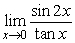 .
.
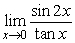 .
.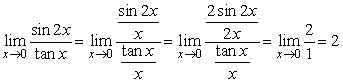
3
Answer true or false. The value of k that makes f continuous for 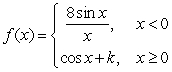 is 7
is 7
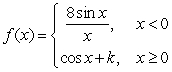 is 7
is 7True
4
Find 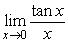 .
.
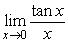 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
5
Find the limit. 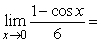
A) 1
B) 6
C) 0
D) +
E) -
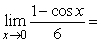
A) 1
B) 6
C) 0
D) +
E) -

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
6
Find the limit. 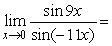
A) 0
B)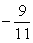
C)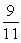
D) +
E) -
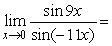
A) 0
B)
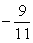
C)
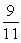
D) +
E) -

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
7
Find 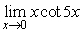 .
.
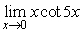 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
8
Find 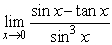 .
.
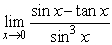 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
9
Find the limit 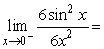
A) 0
B) -1
C) 1
D) +
E) -
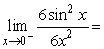
A) 0
B) -1
C) 1
D) +
E) -

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
10
Answer true or false. The Squeeze Theorem can be used to show 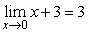 utilizing
utilizing 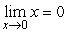 and
and 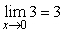 .
.
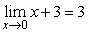 utilizing
utilizing 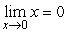 and
and 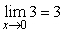 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
11
Answer true or false. The value of k that makes f continuous for 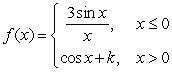 is 2
is 2
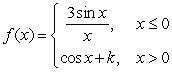 is 2
is 2
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
12
Answer true or false. The Intermediate-Value Theorem can be used to show that the equation x5 = cos x has at least one solution on the interval [-5 /6, 5 /6].

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
13
Find the limit. 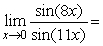
A) 0
B)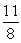
C)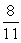
D) 1
E) +
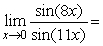
A) 0
B)
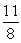
C)
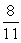
D) 1
E) +

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
14
Find the limit. 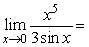
A) 0
B) -1
C) 1
D) +
E) -
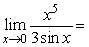
A) 0
B) -1
C) 1
D) +
E) -

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
15
Find the limit. 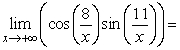
A) 0
B) 1
C) -1
D) +
E) -
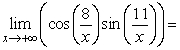
A) 0
B) 1
C) -1
D) +
E) -

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
16
Find the limit 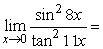
A) 0
B) 1
C)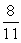
D) +
E) -
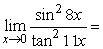
A) 0
B) 1
C)
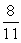
D) +
E) -

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
17
Find all points of discontinuity, if any, for 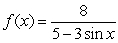
A) 0
B)
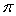
C) 2
D)
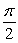
E) None exist
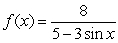
A) 0
B)
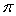
C) 2
D)
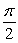
E) None exist

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
18
Find the limit. 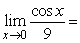
A) 9
B)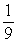
C) 0
D) +
E) -
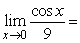
A) 9
B)
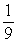
C) 0
D) +
E) -

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
19
Answer true or false. The fact that 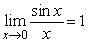 and that
and that 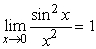 guarantees that
guarantees that 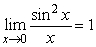 by the Squeeze Theorem.
by the Squeeze Theorem.
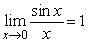 and that
and that 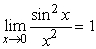 guarantees that
guarantees that 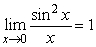 by the Squeeze Theorem.
by the Squeeze Theorem.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
20
Find the limit 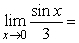
A) 0
B) 1
C) 3
D) +
E) -
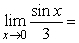
A) 0
B) 1
C) 3
D) +
E) -

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
21
Find 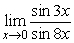 .
.
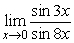 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
22
Find a value for the constant k so that 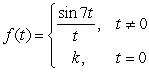 will be continuous at t = 0.
will be continuous at t = 0.
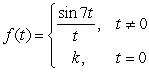 will be continuous at t = 0.
will be continuous at t = 0.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
23
Find 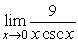 .
.
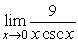 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
24
Find 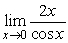 .
.
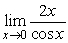 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
25
Find 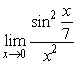 .
.
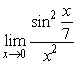 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
26
Find 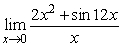 .
.
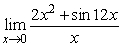 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
27
Find a value for the constant k so that 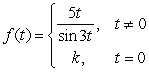 will be continuous at t = 0.
will be continuous at t = 0.
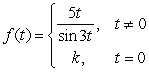 will be continuous at t = 0.
will be continuous at t = 0.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
28
Find 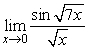 .
.
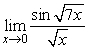 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
29
Find 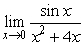 .
.
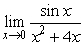 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
30
Find a value for the constant k so that 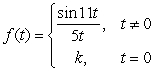 will be continuous at t = 0.
will be continuous at t = 0.
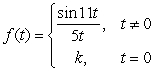 will be continuous at t = 0.
will be continuous at t = 0.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
31
Find 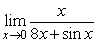 .
.
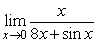 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
32
Find 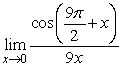 .
.
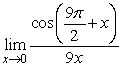 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
33
Find a value for the constant k so that 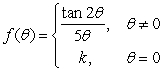 will be continuous at = 0.
will be continuous at = 0.
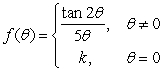 will be continuous at = 0.
will be continuous at = 0. 
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
34
Find 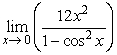 .
.
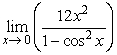 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
35
Find 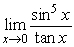 .
.
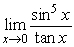 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
36
Find 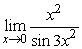 .
.
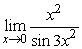 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
37
Find 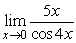 .
.
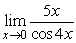 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
38
Find a value for the constant k so that 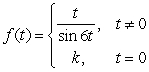 will be continuous at t = 0.
will be continuous at t = 0.
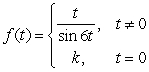 will be continuous at t = 0.
will be continuous at t = 0.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
39
Find a value for the constant k so that 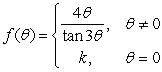 will be continuous at = 0.
will be continuous at = 0.
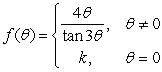 will be continuous at = 0.
will be continuous at = 0. 
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
40
On the interval of [-4, 4], where is f not continuous? ![<strong>On the interval of [-4, 4], where is f not continuous? </strong> A) -2 B) 0 and 2 C) -3 and 1 D) 3 E) Nowhere](https://storage.examlex.com/TB6988/11ead0bc_8e82_b139_99a0_bb45b07abec9_TB6988_00.jpg)
A) -2
B) 0 and 2
C) -3 and 1
D) 3
E) Nowhere
![<strong>On the interval of [-4, 4], where is f not continuous? </strong> A) -2 B) 0 and 2 C) -3 and 1 D) 3 E) Nowhere](https://storage.examlex.com/TB6988/11ead0bc_8e82_b139_99a0_bb45b07abec9_TB6988_00.jpg)
A) -2
B) 0 and 2
C) -3 and 1
D) 3
E) Nowhere

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
41
Answer true or false. The Intermediate-Value Theorem can be used to approximate the locations of all discontinuities for 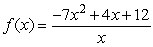 .
.
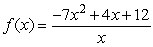 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
42
Show that 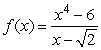 is not a continuous function.
is not a continuous function.
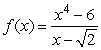 is not a continuous function.
is not a continuous function.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
43
Answer true or false. The function 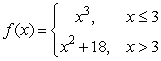 is continuous everywhere.
is continuous everywhere.
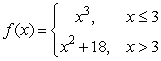 is continuous everywhere.
is continuous everywhere.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
44
Answer true or false. The function 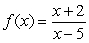 has a removable discontinuity at x = 5.
has a removable discontinuity at x = 5.
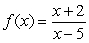 has a removable discontinuity at x = 5.
has a removable discontinuity at x = 5.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
45
Answer true or false. f(x) = x4 - 2x2 + 11 = 0 has at least one solution on the interval [0, 9].

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
46
Answer true or false. f(x) = x2 - 6x + 5 = 0 has at least one solution on the interval [0, 2].

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
47
Find the x-coordinates for all points of discontinuity for 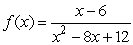 .
.
A) 6 and 2
B) 6
C) -2 and -6
D) -2
E) 2
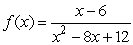 .
.A) 6 and 2
B) 6
C) -2 and -6
D) -2
E) 2

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
48
Answer true or false. f(x) = tan (x4 - 1) has no point of discontinuity.

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
49
Find any points of discontinuity for 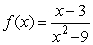 .
.
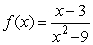 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
50
Find the x-coordinates for all points of discontinuity for 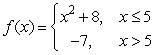 .
.
A) 5
B) 7
C) -5
D) 0 and 7
E) None exists.
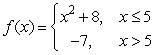 .
.A) 5
B) 7
C) -5
D) 0 and 7
E) None exists.

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
51
A point of discontinuity of 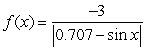 is at
is at
A)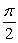
B)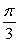
C)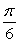
D)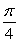
E)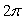
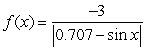 is at
is atA)
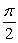
B)
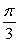
C)
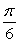
D)
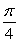
E)
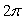

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
52
Find the value of k, if possible, that will make the function continuous. 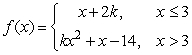
A) -2
B) 6
C) -6
D) 2
E) None exists.
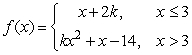
A) -2
B) 6
C) -6
D) 2
E) None exists.

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
53
Define 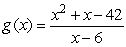 so that it will be continuous everywhere.
so that it will be continuous everywhere.
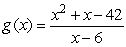 so that it will be continuous everywhere.
so that it will be continuous everywhere.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
54
Answer true or false. f(x) = x5 - 5x4 + 9 has no point of discontinuity.

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
55
Redefine 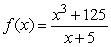 so that it will be continuous everywhere.
so that it will be continuous everywhere.
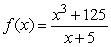 so that it will be continuous everywhere.
so that it will be continuous everywhere.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
56
Use the fact that 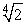 is a solution of x4 - 2 = 0 to approximate
is a solution of x4 - 2 = 0 to approximate 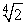 with an error of at most 0.005.
with an error of at most 0.005.
A) 1.169
B) 1.179
C) 1.189
D) 1.199
E) 1.209
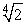 is a solution of x4 - 2 = 0 to approximate
is a solution of x4 - 2 = 0 to approximate 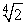 with an error of at most 0.005.
with an error of at most 0.005.A) 1.169
B) 1.179
C) 1.189
D) 1.199
E) 1.209

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
57
Answer true or false. f(x) = |x2 - 4| has points of discontinuity at x = -2 and x = 2.

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
58
Find the x-coordinates for all points of discontinuity for 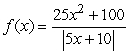 .
.
A) 0
B) -2 and 2
C) -2
D) 2
E) 5
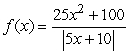 .
.A) 0
B) -2 and 2
C) -2
D) 2
E) 5

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
59
Answer true or false. If f and g are each continuous at c, 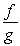 may be discontinuous at c.
may be discontinuous at c.
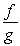 may be discontinuous at c.
may be discontinuous at c.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
60
Find any points of discontinuity for 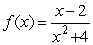 .
.
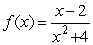 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
61
Assign a value to the constant k which will make g continuous. 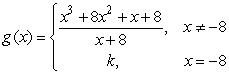
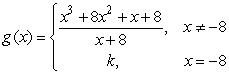

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
62
Find the values of x (if any) at which f is not continuous. f(x) = (x + 8)7.

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
63
Determine the interval for which 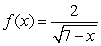 is a continuous function.
is a continuous function.
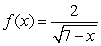 is a continuous function.
is a continuous function.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
64
Show that 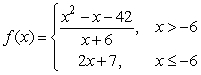 is not continuous at x = -6 but is continuous from the right at x = -6.
is not continuous at x = -6 but is continuous from the right at x = -6.
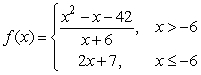 is not continuous at x = -6 but is continuous from the right at x = -6.
is not continuous at x = -6 but is continuous from the right at x = -6.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
65
Determine if the discontinuity at x = 0 in the function 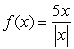 is removable.
is removable.
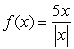 is removable.
is removable.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
66
Given 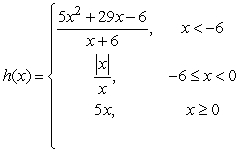 , determine if h is continuous from the right at 0.
, determine if h is continuous from the right at 0.
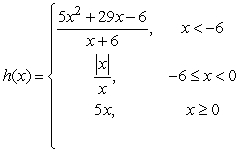 , determine if h is continuous from the right at 0.
, determine if h is continuous from the right at 0.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
67
Determine if the discontinuity at x = 9 in the function 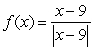 is removable.
is removable.
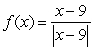 is removable.
is removable.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
68
Prove that 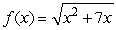 is continuous on [0,+ ).
is continuous on [0,+ ).
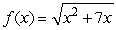 is continuous on [0,+ ).
is continuous on [0,+ ). 
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
69
Find the point of discontinuity in 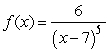 and state whether it is removable.
and state whether it is removable.
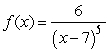 and state whether it is removable.
and state whether it is removable.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
70
Determine if the discontinuity at x = 2 in the function 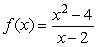 is removable.
is removable.
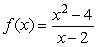 is removable.
is removable.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
71
Show that 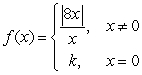 cannot be made continuous for any assigned value of the constant k.
cannot be made continuous for any assigned value of the constant k.
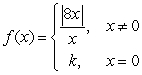 cannot be made continuous for any assigned value of the constant k.
cannot be made continuous for any assigned value of the constant k.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
72
Given 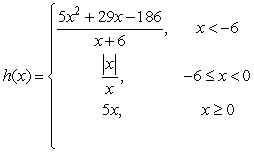 , determine if h is continuous at -6.
, determine if h is continuous at -6.
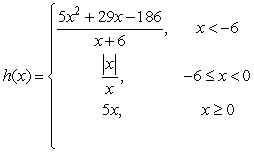 , determine if h is continuous at -6.
, determine if h is continuous at -6.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
73
Find the discontinuities in 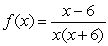 and state whether each is removable or nonremovable.
and state whether each is removable or nonremovable.
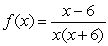 and state whether each is removable or nonremovable.
and state whether each is removable or nonremovable.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
74
Given 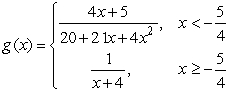 , determine if g is continuous at x =
, determine if g is continuous at x = 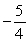 .
.
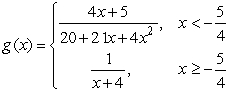 , determine if g is continuous at x =
, determine if g is continuous at x = 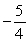 .
.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
75
Assign a value to the constant k which will make f continuous. 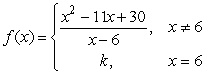
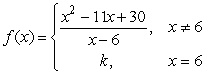

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
76
Show that the equation f(x) = x2 + 3x - 4 has at least one solution in the interval [-5,0].

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
77
Given 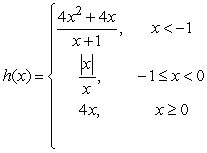 , determine if h is continuous at 0.
, determine if h is continuous at 0.
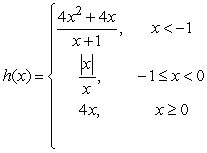 , determine if h is continuous at 0.
, determine if h is continuous at 0.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
78
Show that the equation f(x) = x3 + 8x + 3 has at least one solution in the interval [-2,2].

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
79
Assign a value to the constant k which will make g continuous. 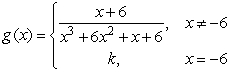
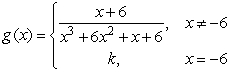

Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck
80
Given 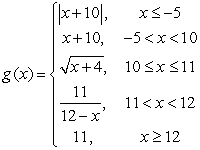 , is g continuous at x = 10.
, is g continuous at x = 10.
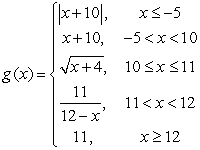 , is g continuous at x = 10.
, is g continuous at x = 10.
Unlock Deck
Unlock for access to all 186 flashcards in this deck.
Unlock Deck
k this deck


