Deck 10: Introduction to Estimation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/152
Play
Full screen (f)
Deck 10: Introduction to Estimation
1
A point estimate consists of a single sample statistic that is used to estimate the true population parameter.
True
2
An interval estimate is a range of values within which the actual value of the population parameter, such as may fall.
True
3
An interval estimate is an estimate of the range for a sample statistic.
False
4
An unbiased estimator is a sample statistic whose expected value equals the population parameter.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
5
The sample proportion  is a consistent estimator of the population proportion p because it is unbiased and the variance of
is a consistent estimator of the population proportion p because it is unbiased and the variance of  is p(1- p) / n, which grows smaller as n grows larger.
is p(1- p) / n, which grows smaller as n grows larger.
 is a consistent estimator of the population proportion p because it is unbiased and the variance of
is a consistent estimator of the population proportion p because it is unbiased and the variance of  is p(1- p) / n, which grows smaller as n grows larger.
is p(1- p) / n, which grows smaller as n grows larger.
Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
6
A specific confidence interval obtained from data will always correctly estimate the population parameter.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
7
An unbiased estimator is said to be consistent if the difference between the estimator and the parameter grows larger as the sample size grows larger.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
8
An estimator is said to be consistent if:
A) the difference between the estimator and the population parameter grows smaller as the sample size grows larger.
B) it is an unbiased estimator.
C) the variance of the estimator is zero.
D) the difference between the estimator and the population parameter stays the same as the sample size grows larger.
A) the difference between the estimator and the population parameter grows smaller as the sample size grows larger.
B) it is an unbiased estimator.
C) the variance of the estimator is zero.
D) the difference between the estimator and the population parameter stays the same as the sample size grows larger.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
9
The sample variance s2 is an unbiased estimator of the population variance 2 when the denominator of s2 is n.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
10
The sample mean 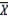 is a consistent estimator of the population mean .
is a consistent estimator of the population mean .
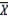 is a consistent estimator of the population mean .
is a consistent estimator of the population mean . 
Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
11
The sample variance (where you divide by n - 1) is an unbiased estimator of the population variance.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following is a characteristic for a good estimator?
A) Being unbiased
B) Being consistent
C) Having relative efficiency
D) All of these choices are true.
A) Being unbiased
B) Being consistent
C) Having relative efficiency
D) All of these choices are true.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
13
The confidence interval estimate of the population mean is constructed around the sample mean.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
14
An unbiased estimator has an average value (across all samples) equal to the population parameter.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
15
Knowing that an estimator is unbiased only assures us that its expected value equals the parameter, but it does not tell us how close the estimator is to the parameter.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
16
The sample variance is a point estimate of the population variance.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
17
An unbiased estimator is said to be consistent if the difference between the estimator and the parameter grows smaller as the sample size grows larger.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
18
An unbiased estimator of a population parameter is defined as:
A) an estimator whose expected value is equal to the parameter.
B) an estimator whose variance is equal to one.
C) an estimator whose expected value is equal to zero.
D) an estimator whose variance goes to zero as the sample size goes to infinity.
A) an estimator whose expected value is equal to the parameter.
B) an estimator whose variance is equal to one.
C) an estimator whose expected value is equal to zero.
D) an estimator whose variance goes to zero as the sample size goes to infinity.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
19
If there are two unbiased estimators of a parameter, the one whose variance is smaller is said to be relatively efficient.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
20
A point estimator is defined as:
A) a range of values that estimates an unknown population parameter.
B) a single value that estimates an unknown population parameter.
C) a range of values that estimates an unknown sample statistic.
D) a single value that estimates an unknown sample statistic.
A) a range of values that estimates an unknown population parameter.
B) a single value that estimates an unknown population parameter.
C) a range of values that estimates an unknown sample statistic.
D) a single value that estimates an unknown sample statistic.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
21
Which of the following statements is correct?
A) The sample mean is an unbiased estimator of the population mean.
B) The sample proportion is an unbiased estimator of the population proportion.
C) The difference between two sample means is an unbiased estimator of the difference between two population means.
D) All of these choices are true.
A) The sample mean is an unbiased estimator of the population mean.
B) The sample proportion is an unbiased estimator of the population proportion.
C) The difference between two sample means is an unbiased estimator of the difference between two population means.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
22
Define consistency.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
23
____________________ estimators do not have the capacity to reflect the effects of larger sample sizes.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
24
Define unbiasedness.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
25
The sample variance s2 is an unbiased estimator of the population variance 2 when the denominator of s2 is
A) n + 1
B) n
C) n -1
D)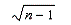
A) n + 1
B) n
C) n -1
D)
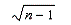

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
26
An interval estimator estimates the value of an unknown ____________________.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
27
The sample ____________________ is relatively more efficient than the sample ____________________ when estimating the population mean.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
28
If there are two unbiased estimators of a population parameter available, the one that has the smallest variance is said to be:
A) a biased estimator.
B) relatively efficient.
C) consistent.
D) relatively unbiased.
A) a biased estimator.
B) relatively efficient.
C) consistent.
D) relatively unbiased.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
29
____________________ estimators reflect the effects of larger sample sizes, but ____________________ estimators do not.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
30
Draw a sampling distribution of an unbiased estimator for .

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
31
The version of the sample variance where you divide by ____________________ gives you an unbiased estimator of the population variance.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
32
If there are two unbiased estimators of the same parameter, the one whose variance is smaller is said to be relatively more ____________________.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
33
A(n) ____________________ estimator of a population parameter is an estimator whose expected value is equal to that parameter.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
34
The librarian at the New York City Public Library has asked her assistant for an interval estimate of the mean number of books checked out each day.The assistant took a sample and found the mean to be 880 books.She provides the librarian with an interval estimate of between 790 and 970 books checked out per day.An efficient, unbiased point estimate of the number of books checked out each day at the New York City Public Library is:
A) 790
B) 880
C) 90
D) None of these choices.
A) 790
B) 880
C) 90
D) None of these choices.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
35
Is the sample mean a consistent estimator of the population mean? Explain

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
36
It is intuitively reasonable to expect that a larger sample will produce more ____________________ results.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
37
The sample ____________________ is an unbiased estimator for the population mean.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
38
An unbiased estimator is ____________________ if its variance gets smaller as n gets larger.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
39
The problem with relying on a point estimate of a population parameter is that:
A) it is virtually certain to be wrong.
B) it doesn't have the capacity to reflect the effects of larger sample sizes.
C) it doesn't tell us how close or far the point estimate might be from the parameter.
D) All of these choices are true.
A) it is virtually certain to be wrong.
B) it doesn't have the capacity to reflect the effects of larger sample sizes.
C) it doesn't tell us how close or far the point estimate might be from the parameter.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
40
Which of the following statements is true?
A) The sample mean is relatively more efficient than the sample median.
B) The version of the sample variance where you divide by n is biased.
C) The sample mean is consistent.
D) All of these choices are true.
A) The sample mean is relatively more efficient than the sample median.
B) The version of the sample variance where you divide by n is biased.
C) The sample mean is consistent.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
41
Draw sampling distributions of a consistent estimator for where one sample mean is larger than the other.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
42
In the formula 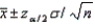 , the subscript / 2 refers to the area in the lower tail or upper tail of the sampling distribution of the sample mean.
, the subscript / 2 refers to the area in the lower tail or upper tail of the sampling distribution of the sample mean.
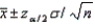 , the subscript / 2 refers to the area in the lower tail or upper tail of the sampling distribution of the sample mean.
, the subscript / 2 refers to the area in the lower tail or upper tail of the sampling distribution of the sample mean. 
Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
43
A confidence interval is an interval estimate for which there is a specified degree of certainty that the actual value of the population parameter will fall within the interval.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
44
A 95% confidence interval estimate for a population mean is determined to be 75 to 85.If the confidence level is reduced to 80%, the confidence interval for becomes wider.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
45
The larger the confidence level used in constructing a confidence interval estimate of the population mean, the narrower the confidence interval.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
46
Suppose that a 90% confidence interval for is given by 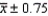 .This notation means that we are 90% confident that falls between
.This notation means that we are 90% confident that falls between 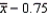 and
and 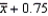 .
.
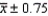 .This notation means that we are 90% confident that falls between
.This notation means that we are 90% confident that falls between 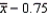 and
and 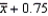 .
. 
Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
47
One can reduce the width of a confidence interval by taking a smaller sample size.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
48
Draw a sampling distribution of a biased estimator for .

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
49
The width of a 95% confidence interval is 0.95.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
50
In developing an interval estimate for a population mean, the population standard deviation 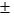 was assumed to be 8.The interval estimate was 50.0 11ef1773_82b8_7818_8934_fd6931bff87b_TB7453_112.50.Had equaled 16, the interval estimate would be 10011ef1773_82b8_7818_8934_fd6931bff87b_TB7453_11 5.0.
was assumed to be 8.The interval estimate was 50.0 11ef1773_82b8_7818_8934_fd6931bff87b_TB7453_112.50.Had equaled 16, the interval estimate would be 10011ef1773_82b8_7818_8934_fd6931bff87b_TB7453_11 5.0.
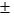 was assumed to be 8.The interval estimate was 50.0 11ef1773_82b8_7818_8934_fd6931bff87b_TB7453_112.50.Had equaled 16, the interval estimate would be 10011ef1773_82b8_7818_8934_fd6931bff87b_TB7453_11 5.0.
was assumed to be 8.The interval estimate was 50.0 11ef1773_82b8_7818_8934_fd6931bff87b_TB7453_112.50.Had equaled 16, the interval estimate would be 10011ef1773_82b8_7818_8934_fd6931bff87b_TB7453_11 5.0. 
Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
51
When constructing confidence interval for a parameter, we generally set the confidence level 1 - close to 1 (usually between 0.90 and 0.99) because it is the probability that the interval includes the actual value of the population parameter.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
52
The term 1 - refers to the probability that a confidence interval does not contain the population parameter.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
53
Draw the sampling distribution of two unbiased estimators for , one of which is relatively efficient.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
54
In order to construct a confidence interval estimate of the population mean, the value of the population mean is needed.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
55
Define relative efficiency.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
56
A random sample of 10 university students was surveyed to help estimate the average amount of time students spent per week on their computers.The student hours spent using a personal computer over a randomly selected week were 13, 14, 5, 6, 8, 10, 7, 12, 15, 3.
a.
Find an unbiased estimator of the average time per week for all university students.
b.
Find an unbiased estimator of the variance.
c.
Find a consistent estimator of the average time per week for all university students.
a.
Find an unbiased estimator of the average time per week for all university students.
b.
Find an unbiased estimator of the variance.
c.
Find a consistent estimator of the average time per week for all university students.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
57
Explain briefly why interval estimators are preferred to point estimators.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
58
The difference between the sample statistic and actual value of the population parameter is the confidence level of the estimate.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
59
We cannot interpret the confidence interval estimate of as a probability statement about because the population mean is a fixed quantity.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
60
The width of the confidence interval estimate of the population mean is a function of only two quantities: the population standard deviation and the sample size n.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
61
The lower limit of the 90% confidence interval for , where n = 64,  = 70, and = 20, is 65.89.
= 70, and = 20, is 65.89.
 = 70, and = 20, is 65.89.
= 70, and = 20, is 65.89. 
Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
62
Doubling the population standard deviation has the effect of doubling the width of the confidence interval estimate of .

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
63
In developing an interval estimate for a population mean, a sample of 50 observations was used.The interval estimate was 19.76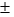 1.32.Had the sample size been 200 instead of 50, the interval estimate would have been:
1.32.Had the sample size been 200 instead of 50, the interval estimate would have been:
A) 19.7611ef1774_af29_76ab_8934_639a69e0ae9d_TB7453_11 .33
B) 19.76 11ef1774_af29_76ab_8934_639a69e0ae9d_TB7453_11 .66
C) 19.76 11ef1774_af29_76ab_8934_639a69e0ae9d_TB7453_11 5.28
D) None of these choices.
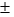 1.32.Had the sample size been 200 instead of 50, the interval estimate would have been:
1.32.Had the sample size been 200 instead of 50, the interval estimate would have been:A) 19.7611ef1774_af29_76ab_8934_639a69e0ae9d_TB7453_11 .33
B) 19.76 11ef1774_af29_76ab_8934_639a69e0ae9d_TB7453_11 .66
C) 19.76 11ef1774_af29_76ab_8934_639a69e0ae9d_TB7453_11 5.28
D) None of these choices.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
64
The width of a confidence interval estimate of the population mean increases when the:
A) level of confidence increases
B) sample size decreases
C) value of the population standard deviation increases
D) All of these choices are true.
A) level of confidence increases
B) sample size decreases
C) value of the population standard deviation increases
D) All of these choices are true.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
65
The letter in the formula for constructing a confidence interval estimate of the population mean is:
A) the level of confidence.
B) the probability that a particular confidence interval will contain the population mean.
C) the area in the lower tail of the sampling distribution of the sample mean.
D) None of these choices.
A) the level of confidence.
B) the probability that a particular confidence interval will contain the population mean.
C) the area in the lower tail of the sampling distribution of the sample mean.
D) None of these choices.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
66
Other things being equal, as the confidence level increases, the width of the confidence interval increases.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
67
The term 1- 0 refers to:
A) the probability that a confidence interval does not contain the population parameter.
B) the confidence level.
C) the level of unbiasedness.
D) the level of consistency.
A) the probability that a confidence interval does not contain the population parameter.
B) the confidence level.
C) the level of unbiasedness.
D) the level of consistency.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
68
If the confidence level is reduced, the confidence interval:
A) widens.
B) remains the same.
C) narrows.
D) disappears.
A) widens.
B) remains the same.
C) narrows.
D) disappears.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
69
Which of the following is an incorrect statement about a 90% confidence interval?
A) If we repeatedly draw samples of the same size from the same population, 90% of the resulting confidence intervals will include .
B) There is a 90% probability that the population mean will lie between the lower confidence limit (LCL) and the upper confidence limit (UCL).
C) We are 90% confident that our sample mean equals the population mean .
D) 90% of the population values will lie within the confidence interval.
A) If we repeatedly draw samples of the same size from the same population, 90% of the resulting confidence intervals will include .
B) There is a 90% probability that the population mean will lie between the lower confidence limit (LCL) and the upper confidence limit (UCL).
C) We are 90% confident that our sample mean equals the population mean .
D) 90% of the population values will lie within the confidence interval.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
70
Other things being equal, the confidence interval for the mean will be wider for 99% confidence than for 95% confidence.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
71
In developing an interval estimate for a population mean, the population standard deviation was assumed to be 10.The interval estimate was 50.92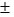 2.14.Had equaled 20, the interval estimate would be
2.14.Had equaled 20, the interval estimate would be
A) 60.92 11ef1774_80bc_3d7a_8934_51736afba8b4_TB7453_11 2.14
B) 50.9211ef1774_80bc_3d7a_8934_51736afba8b4_TB7453_11 12.14
C) 101.84 11ef1774_80bc_3d7a_8934_51736afba8b4_TB7453_11 4.28
D) 50.92 11ef1774_80bc_3d7a_8934_51736afba8b4_TB7453_11 4.28
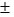 2.14.Had equaled 20, the interval estimate would be
2.14.Had equaled 20, the interval estimate would beA) 60.92 11ef1774_80bc_3d7a_8934_51736afba8b4_TB7453_11 2.14
B) 50.9211ef1774_80bc_3d7a_8934_51736afba8b4_TB7453_11 12.14
C) 101.84 11ef1774_80bc_3d7a_8934_51736afba8b4_TB7453_11 4.28
D) 50.92 11ef1774_80bc_3d7a_8934_51736afba8b4_TB7453_11 4.28

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
72
Suppose an interval estimate for the population mean was 62.84 to 69.46.The population standard deviation was assumed to be 6.50, and a sample of 100 observations was used.The mean of the sample was:
A) 6.62
B) 56.34
C) 62.96
D) 66.15
A) 6.62
B) 56.34
C) 62.96
D) 66.15

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
73
After constructing a confidence interval estimate for a population mean, you believe that the interval is useless because it is too wide.In order to correct this problem, you need to:
A) increase the sample size.
B) increase the population standard deviation.
C) increase the level of confidence.
D) increase the sample mean.
A) increase the sample size.
B) increase the population standard deviation.
C) increase the level of confidence.
D) increase the sample mean.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
74
Increasing the value of 1- narrows a confidence interval.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
75
Suppose that a 95% confidence interval for is given by 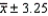 .This notation means that, if we repeatedly draw samples of the same size from the same population, 95% of the values of
.This notation means that, if we repeatedly draw samples of the same size from the same population, 95% of the values of  will be such that would lie somewhere between
will be such that would lie somewhere between 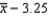 and
and 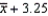 .
.
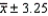 .This notation means that, if we repeatedly draw samples of the same size from the same population, 95% of the values of
.This notation means that, if we repeatedly draw samples of the same size from the same population, 95% of the values of  will be such that would lie somewhere between
will be such that would lie somewhere between 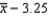 and
and 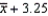 .
. 
Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
76
The 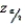 value for a 95% confidence interval estimate for a population mean is
value for a 95% confidence interval estimate for a population mean is
A) 0.95
B) 0.025
C) 1.65
D) 1.96
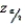 value for a 95% confidence interval estimate for a population mean is
value for a 95% confidence interval estimate for a population mean isA) 0.95
B) 0.025
C) 1.65
D) 1.96

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
77
In this chapter you need four values to construct the confidence interval estimate of .They are the sample mean, the sample size, the population standard deviation, and the confidence level.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
78
When constructing confidence interval estimate of , doubling the sample size n decreases the width of the interval by half.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
79
Suppose a sample size of 5 has mean 9.60.If the population variance is 5 and the population is normally distributed, the lower limit for a 92% confidence interval is 7.85.

Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck
80
Given a mean of 2.1 and a standard deviation of 0.7, a 90% confidence interval will be 2.1 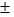 0.7.
0.7.
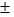 0.7.
0.7.
Unlock Deck
Unlock for access to all 152 flashcards in this deck.
Unlock Deck
k this deck


