Deck 11: Comparisons Involving Proportions and a Test of Independence
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/99
Play
Full screen (f)
Deck 11: Comparisons Involving Proportions and a Test of Independence
1
Exhibit 11-2
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 11-2. The expected number of freshmen is
A) 83
B) 90
C) 30
D) 10
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 11-2. The expected number of freshmen is
A) 83
B) 90
C) 30
D) 10
90
2
A population where each element of the population is assigned to one and only one of several classes or categories is a
A) multinomial population
B) Poisson population
C) normal population
D) None of these alternatives is correct.
A) multinomial population
B) Poisson population
C) normal population
D) None of these alternatives is correct.
A
3
Exhibit 11-1
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained.
Do you support capital punishment?
We are interested in determining whether or not the opinions of the individuals as to Yes, No, and No Opinion) are uniformly distributed.
-Refer to Exhibit 11-1. The number of degrees of freedom associated with this problem is
A) 150
B) 149
C) 2
D) 3
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained.
Do you support capital punishment?
We are interested in determining whether or not the opinions of the individuals as to Yes, No, and No Opinion) are uniformly distributed.
-Refer to Exhibit 11-1. The number of degrees of freedom associated with this problem is
A) 150
B) 149
C) 2
D) 3
2
4
A statistical test conducted to determine whether to reject or not reject a hypothesized probability distribution for a population is known as a
A) contingency test
B) probability test
C) goodness of fit test
D) None of these alternatives is correct.
A) contingency test
B) probability test
C) goodness of fit test
D) None of these alternatives is correct.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
5
The degrees of freedom for a contingency table with 10 rows and 11 columns is
A) 100
B) 110
C) 21
D) 90
A) 100
B) 110
C) 21
D) 90

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
6
If we are interested in testing whether the proportion of items in population 1 is larger than the proportion of items in population 2, the
A) null hypothesis should state P1 - P2 < 0
B) null hypothesis should state P1 - P2 > 0
C) alternative hypothesis should state P1 - P2 > 0
D) alternative hypothesis should state P1 - P2 < 0
A) null hypothesis should state P1 - P2 < 0
B) null hypothesis should state P1 - P2 > 0
C) alternative hypothesis should state P1 - P2 > 0
D) alternative hypothesis should state P1 - P2 < 0

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
7
Exhibit 11-1
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained.
Do you support capital punishment?
We are interested in determining whether or not the opinions of the individuals as to Yes, No, and No Opinion) are uniformly distributed.
-Refer to Exhibit 11-1. The conclusion of the test at 95% confidence) is that the
A) distribution is uniform
B) distribution is not uniform
C) test is inconclusive
D) None of these alternatives is correct.
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained.
Do you support capital punishment?
We are interested in determining whether or not the opinions of the individuals as to Yes, No, and No Opinion) are uniformly distributed.
-Refer to Exhibit 11-1. The conclusion of the test at 95% confidence) is that the
A) distribution is uniform
B) distribution is not uniform
C) test is inconclusive
D) None of these alternatives is correct.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
8
A goodness of fit test is always conducted as a
A) lower-tail test
B) upper-tail test
C) middle test
D) None of these alternatives is correct.
A) lower-tail test
B) upper-tail test
C) middle test
D) None of these alternatives is correct.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
9
In order not to violate the requirements necessary to use the chi-square distribution, each expected frequency in a goodness of fit test must be
A) at least 5
B) at least 10
C) no more than 5
D) less than 2
A) at least 5
B) at least 10
C) no more than 5
D) less than 2

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
10
The degrees of freedom for a contingency table with 6 rows and 3 columns is
A) 18
B) 15
C) 6
D) 10
A) 18
B) 15
C) 6
D) 10

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
11
An important application of the chi-square distribution is
A) making inferences about a single population variance
B) testing for goodness of fit
C) testing for the independence of two variables
D) All of these alternatives are correct.
A) making inferences about a single population variance
B) testing for goodness of fit
C) testing for the independence of two variables
D) All of these alternatives are correct.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
12
Exhibit 11-1
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained.
Do you support capital punishment?
We are interested in determining whether or not the opinions of the individuals as to Yes, No, and No Opinion) are uniformly distributed.
-Refer to Exhibit 11-1. The calculated value for the test statistic equals
A) 2
B) -2
C) 20
D) 4
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained.
Do you support capital punishment?
We are interested in determining whether or not the opinions of the individuals as to Yes, No, and No Opinion) are uniformly distributed.
-Refer to Exhibit 11-1. The calculated value for the test statistic equals
A) 2
B) -2
C) 20
D) 4

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
13
The sampling distribution of is approximated by a
A) normal distribution
B) t-distribution with n1 + n2 degrees of freedom
C) t-distribution with n1 + n2 - 1 degrees of freedom
D) t-distribution with n1 + n2 + 2 degrees of freedom
A) normal distribution
B) t-distribution with n1 + n2 degrees of freedom
C) t-distribution with n1 + n2 - 1 degrees of freedom
D) t-distribution with n1 + n2 + 2 degrees of freedom

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
14
The sampling distribution for a goodness of fit test is the
A) Poisson distribution
B) t distribution
C) normal distribution
D) chi-square distribution
A) Poisson distribution
B) t distribution
C) normal distribution
D) chi-square distribution

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
15
Exhibit 11-1
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained.
Do you support capital punishment?
We are interested in determining whether or not the opinions of the individuals as to Yes, No, and No Opinion) are uniformly distributed.
-Refer to Exhibit 11-1. The expected frequency for each group is
A) 0.333
B) 0.50
C) 1/3
D) 50
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained.
Do you support capital punishment?
We are interested in determining whether or not the opinions of the individuals as to Yes, No, and No Opinion) are uniformly distributed.
-Refer to Exhibit 11-1. The expected frequency for each group is
A) 0.333
B) 0.50
C) 1/3
D) 50

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
16
The number of degrees of freedom for the appropriate chi-square distribution in a test of independence is
A) n-1
B) K-1
C) number of rows minus 1 times number of columns minus 1
D) a chi-square distribution is not used
A) n-1
B) K-1
C) number of rows minus 1 times number of columns minus 1
D) a chi-square distribution is not used

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
17
Exhibit 11-2
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 11-2. The expected frequency of seniors is
A) 60
B) 20%
C) 68
D) 64
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 11-2. The expected frequency of seniors is
A) 60
B) 20%
C) 68
D) 64

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
18
Exhibit 11-1
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained.
Do you support capital punishment?
We are interested in determining whether or not the opinions of the individuals as to Yes, No, and No Opinion) are uniformly distributed.
-Refer to Exhibit 11-1. The p-value is
A) larger than 0.1
B) less than 0.1
C) less than 0.05
D) larger than 0.9
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained.
Do you support capital punishment?
We are interested in determining whether or not the opinions of the individuals as to Yes, No, and No Opinion) are uniformly distributed.
-Refer to Exhibit 11-1. The p-value is
A) larger than 0.1
B) less than 0.1
C) less than 0.05
D) larger than 0.9

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
19
Exhibit 11-2
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 11-2. The calculated value for the test statistic equals
A) 0.5444
B) 300
C) 1.6615
D) 6.6615
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 11-2. The calculated value for the test statistic equals
A) 0.5444
B) 300
C) 1.6615
D) 6.6615

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
20
The degrees of freedom for a contingency table with 12 rows and 12 columns is
A) 144
B) 121
C) 12
D) 120
A) 144
B) 121
C) 12
D) 120

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
21
Exhibit 11-2
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 11-2. The p-value is
A) less than .005
B) between .025 and 0.05
C) between .05 and 0.1
D) greater than 0.1
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 11-2. The p-value is
A) less than .005
B) between .025 and 0.05
C) between .05 and 0.1
D) greater than 0.1

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
22
Exhibit 11-6
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal.
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-Refer to Exhibit 11-6. The calculated value for the test statistic equals
A) 300
B) 4
C) 0
D) 8
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal.
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-Refer to Exhibit 11-6. The calculated value for the test statistic equals
A) 300
B) 4
C) 0
D) 8

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
23
Exhibit 11-2
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 11-2. At 95% confidence, the null hypothesis
A) should not be rejected
B) should be rejected
C) was designed wrong
D) None of these alternatives is correct.
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification.
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year.
-Refer to Exhibit 11-2. At 95% confidence, the null hypothesis
A) should not be rejected
B) should be rejected
C) was designed wrong
D) None of these alternatives is correct.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
24
Exhibit 11-3
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 11-3. The expected frequency of those who received medication and were cured is
A) 70
B) 150
C) 28
D) 48
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 11-3. The expected frequency of those who received medication and were cured is
A) 70
B) 150
C) 28
D) 48

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
25
Exhibit 11-5
The table below gives beverage preferences for random samples of teens and adults.
We are asked to test for independence between age i.e., adult and teen) and drink preferences.
-Refer to Exhibit 11-5. With a .05 level of significance, the critical value for the test is
A) 1.645
B) 7.815
C) 14.067
D) 15.507
The table below gives beverage preferences for random samples of teens and adults.
We are asked to test for independence between age i.e., adult and teen) and drink preferences.
-Refer to Exhibit 11-5. With a .05 level of significance, the critical value for the test is
A) 1.645
B) 7.815
C) 14.067
D) 15.507

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
26
Exhibit 11-3
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 11-3. The hypothesis is to be tested at the 5% level of significance. The critical value from the table equals
A) 3.84
B) 7.81
C) 5.99
D) 9.34
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 11-3. The hypothesis is to be tested at the 5% level of significance. The critical value from the table equals
A) 3.84
B) 7.81
C) 5.99
D) 9.34

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
27
Exhibit 11-4
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. The p-value is
A) greater than 0.1
B) between 0.05 and 0.1
C) between 0.025 and 0.05
D) between 0.01 and .025
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. The p-value is
A) greater than 0.1
B) between 0.05 and 0.1
C) between 0.025 and 0.05
D) between 0.01 and .025

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
28
Exhibit 11-4
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. The expected frequency for the Business College is
A) 0.3
B) 0.35
C) 90
D) 105
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. The expected frequency for the Business College is
A) 0.3
B) 0.35
C) 90
D) 105

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
29
Exhibit 11-3
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 11-3. The number of degrees of freedom associated with this problem is
A) 4
B) 149
C) 1
D) 3
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 11-3. The number of degrees of freedom associated with this problem is
A) 4
B) 149
C) 1
D) 3

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
30
Exhibit 11-5
The table below gives beverage preferences for random samples of teens and adults.
We are asked to test for independence between age i.e., adult and teen) and drink preferences.
-Refer to Exhibit 11-5. The test statistic for this test of independence is
A) 0
B) 8.4
C) 62.5
D) 82.5
The table below gives beverage preferences for random samples of teens and adults.
We are asked to test for independence between age i.e., adult and teen) and drink preferences.
-Refer to Exhibit 11-5. The test statistic for this test of independence is
A) 0
B) 8.4
C) 62.5
D) 82.5

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
31
Exhibit 11-6
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal.
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-Refer to Exhibit 11-6. The expected frequency for each group is
A) 0.333
B) 0.50
C) 50
D) None of these alternatives is correct.
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal.
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-Refer to Exhibit 11-6. The expected frequency for each group is
A) 0.333
B) 0.50
C) 50
D) None of these alternatives is correct.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
32
Exhibit 11-4
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. This problem is an example of a
A) normally distributed variable
B) test for independence
C) Poisson distributed variable
D) multinomial population
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. This problem is an example of a
A) normally distributed variable
B) test for independence
C) Poisson distributed variable
D) multinomial population

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
33
Exhibit 11-3
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 11-3. The p-value is
A) less than .005
B) between .005 and .01
C) between .01 and .025
D) between .025 and .05
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 11-3. The p-value is
A) less than .005
B) between .005 and .01
C) between .01 and .025
D) between .025 and .05

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
34
Exhibit 11-4
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. The hypothesis is to be tested at the 5% level of significance. The critical value from the table equals
A) 1.645
B) 1.96
C) 5.991
D) 7.815
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. The hypothesis is to be tested at the 5% level of significance. The critical value from the table equals
A) 1.645
B) 1.96
C) 5.991
D) 7.815

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
35
Exhibit 11-4
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. The conclusion of the test is that the
A) proportions have changed significantly
B) proportions have not changed significantly
C) test is inconclusive
D) None of these alternatives is correct.
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. The conclusion of the test is that the
A) proportions have changed significantly
B) proportions have not changed significantly
C) test is inconclusive
D) None of these alternatives is correct.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
36
Exhibit 11-5
The table below gives beverage preferences for random samples of teens and adults.
We are asked to test for independence between age i.e., adult and teen) and drink preferences.
-Refer to Exhibit 11-5. The expected number of adults who prefer coffee is
A) 0.25
B) 0.33
C) 150
D) 200
The table below gives beverage preferences for random samples of teens and adults.
We are asked to test for independence between age i.e., adult and teen) and drink preferences.
-Refer to Exhibit 11-5. The expected number of adults who prefer coffee is
A) 0.25
B) 0.33
C) 150
D) 200

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
37
Exhibit 11-4
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. The calculated value for the test statistic equals
A) 0.01
B) 0.75
C) 4.29
D) 4.38
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College.
Refer to Exhibit 11-4. The calculated value for the test statistic equals
A) 0.01
B) 0.75
C) 4.29
D) 4.38

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
38
Exhibit 11-3
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 11-3. The test statistic is
A) 10.08
B) 54.02
C) 1.96
D) 1.645
In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below.
We are interested in determining whether or not the medication was effective in curing the common cold.
-Refer to Exhibit 11-3. The test statistic is
A) 10.08
B) 54.02
C) 1.96
D) 1.645

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
39
Exhibit 11-6
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal.
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-Refer to Exhibit 11-6. The number of degrees of freedom associated with this problem is
A) 2
B) 3
C) 300
D) 299
The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal.
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed.
-Refer to Exhibit 11-6. The number of degrees of freedom associated with this problem is
A) 2
B) 3
C) 300
D) 299

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
40
Exhibit 11-5
The table below gives beverage preferences for random samples of teens and adults.
We are asked to test for independence between age i.e., adult and teen) and drink preferences.
-Refer to Exhibit 11-5. The p-value is
A) between .1 and .05
B) between .05 and .025
C) between .025 and .01
D) less than 0.005
The table below gives beverage preferences for random samples of teens and adults.
We are asked to test for independence between age i.e., adult and teen) and drink preferences.
-Refer to Exhibit 11-5. The p-value is
A) between .1 and .05
B) between .05 and .025
C) between .025 and .01
D) less than 0.005

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
41
Exhibit 11-7
The results of a recent poll on the preference of shoppers regarding two products are shown below.
-Refer to Exhibit 11-7. The 95% confidence interval estimate for the difference between the populations favoring the products is
A) -0.024 to 0.064
B) 0.6 to 0.7
C) 0.024 to 0.7
D) 0.02 to 0.3
The results of a recent poll on the preference of shoppers regarding two products are shown below.
-Refer to Exhibit 11-7. The 95% confidence interval estimate for the difference between the populations favoring the products is
A) -0.024 to 0.064
B) 0.6 to 0.7
C) 0.024 to 0.7
D) 0.02 to 0.3

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
42
Exhibit 11-9
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-Refer to Exhibit 11-9. The 95% confidence interval for the difference between the two proportions is
A) 384 to 450
B) 0.48 to 0.5
C) 0.028 to 0.068
D) -0.068 to 0.028
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-Refer to Exhibit 11-9. The 95% confidence interval for the difference between the two proportions is
A) 384 to 450
B) 0.48 to 0.5
C) 0.028 to 0.068
D) -0.068 to 0.028

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
43
Exhibit 11-8
An insurance company selected samples of clients under 18 years of age and over 18 and recorded the number of accidents they had in the previous year. The results are shown below.
We are interested in determining if the accident proportions differ between the two age groups.
-Refer to Exhibit 11-8. The test statistic is
A) 0.96
B) 1.96
C) 2.96
D) 3.96
An insurance company selected samples of clients under 18 years of age and over 18 and recorded the number of accidents they had in the previous year. The results are shown below.
We are interested in determining if the accident proportions differ between the two age groups.
-Refer to Exhibit 11-8. The test statistic is
A) 0.96
B) 1.96
C) 2.96
D) 3.96

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
44
Among a sample of 50 M.D.'s medical doctors) in the city of Memphis, Tennessee, 10 indicated they make house calls; while among a sample of 100 M.D.'s in Atlanta, Georgia, 18 said they make house calls. Determine a 95% interval estimate for the difference between the proportion of doctors who make house calls in the two cities.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
45
A comparative study of organic and conventionally grown produce was checked for the presence of E. coli. Results are summarized below. Is there a significant difference in the proportion of E. Coli in organic vs. conventionally grown produce? Test at ? = 0.10.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
46
Of 200 UTC seniors surveyed, 60 were planning on attending Graduate School. At UTK, 400 seniors were surveyed and 100 indicated that they were planning to attend Graduate School.
a. Determine a 95% confidence interval estimate for the difference between the proportion of seniors at the two universities that were planning to attend Graduate School.
b. Is there conclusive evidence to prove that the proportion of students from UTC who plan to go to Graduate School is significantly more than those from UTK? Explain.
a. Determine a 95% confidence interval estimate for the difference between the proportion of seniors at the two universities that were planning to attend Graduate School.
b. Is there conclusive evidence to prove that the proportion of students from UTC who plan to go to Graduate School is significantly more than those from UTK? Explain.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
47
Of 300 female registered voters surveyed, 120 indicated they were planning to vote for the incumbent president; while of 400 male registered voters, 140 indicated they were planning to vote for the incumbent president.
a. Compute the test statistic.
b. At alpha = .05, test to see if there is a significant difference between the proportions of females and males who plan to vote for the incumbent president. Use the p-value approach.)
a. Compute the test statistic.
b. At alpha = .05, test to see if there is a significant difference between the proportions of females and males who plan to vote for the incumbent president. Use the p-value approach.)

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
48
Exhibit 11-8
An insurance company selected samples of clients under 18 years of age and over 18 and recorded the number of accidents they had in the previous year. The results are shown below.
We are interested in determining if the accident proportions differ between the two age groups.
-Refer to Exhibit 11-8. The pooled proportion is
A) 0.305
B) 0.300
C) 0.027
D) 0.450
An insurance company selected samples of clients under 18 years of age and over 18 and recorded the number of accidents they had in the previous year. The results are shown below.
We are interested in determining if the accident proportions differ between the two age groups.
-Refer to Exhibit 11-8. The pooled proportion is
A) 0.305
B) 0.300
C) 0.027
D) 0.450

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
49
Exhibit 11-9
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-We are interested in testing the following hypotheses. H0: P1- P2 = 0 Ha: P1- P2 ? 0
The test statistic Z is computed to be 2.0. The p-value for this test is
A) 0.9772
B) 1.9544
C) 0.0228
D) 0.0456
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-We are interested in testing the following hypotheses. H0: P1- P2 = 0 Ha: P1- P2 ? 0
The test statistic Z is computed to be 2.0. The p-value for this test is
A) 0.9772
B) 1.9544
C) 0.0228
D) 0.0456

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
50
Exhibit 11-8
An insurance company selected samples of clients under 18 years of age and over 18 and recorded the number of accidents they had in the previous year. The results are shown below.
We are interested in determining if the accident proportions differ between the two age groups.
-Refer to Exhibit 11-8 and let pu represent the proportion under and po the proportion over the age of 18. The null hypothesis is
A) pu - po ? 0.
B) pu - po ? 0 .
C) pu - po ? 0
D) pu - po = 0
An insurance company selected samples of clients under 18 years of age and over 18 and recorded the number of accidents they had in the previous year. The results are shown below.
We are interested in determining if the accident proportions differ between the two age groups.
-Refer to Exhibit 11-8 and let pu represent the proportion under and po the proportion over the age of 18. The null hypothesis is
A) pu - po ? 0.
B) pu - po ? 0 .
C) pu - po ? 0
D) pu - po = 0

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
51
Exhibit 11-7
The results of a recent poll on the preference of shoppers regarding two products are shown below.
-Refer to Exhibit 11-7. At 95% confidence, the margin of error is
A) 0.064
B) 0.044
C) 0.0225
D) 52
The results of a recent poll on the preference of shoppers regarding two products are shown below.
-Refer to Exhibit 11-7. At 95% confidence, the margin of error is
A) 0.064
B) 0.044
C) 0.0225
D) 52

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
52
Exhibit 11-8
An insurance company selected samples of clients under 18 years of age and over 18 and recorded the number of accidents they had in the previous year. The results are shown below.
We are interested in determining if the accident proportions differ between the two age groups.
-Refer to Exhibit 11-8. The p-value is
A) less than 0.001
B) more than 0.10
C) 0.0228
D) 0.3
An insurance company selected samples of clients under 18 years of age and over 18 and recorded the number of accidents they had in the previous year. The results are shown below.
We are interested in determining if the accident proportions differ between the two age groups.
-Refer to Exhibit 11-8. The p-value is
A) less than 0.001
B) more than 0.10
C) 0.0228
D) 0.3

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
53
During the primary elections of 1996, candidate A showed the following pre-election voter support in Tennessee and Mississippi.
Voters Surveyed Voters Favoring Candidate A
Tennessee 500 295
Mississippi 700 357
a. Develop a 95% confidence interval estimate for the difference between the proportion of voters favoring candidate A in the two states.
b. Is there conclusive evidence that one of the two states had a larger proportion of voters' support? If yes, which state? Explain.
Voters Surveyed Voters Favoring Candidate A
Tennessee 500 295
Mississippi 700 357
a. Develop a 95% confidence interval estimate for the difference between the proportion of voters favoring candidate A in the two states.
b. Is there conclusive evidence that one of the two states had a larger proportion of voters' support? If yes, which state? Explain.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
54
Exhibit 11-9
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-For a one-tailed test lower tail) at 99.7% confidence, Z =
A) ± 1.86
B) - 2.75
C) ±1.96
D) -1.645
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-For a one-tailed test lower tail) at 99.7% confidence, Z =
A) ± 1.86
B) - 2.75
C) ±1.96
D) -1.645

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
55
Of 150 Chattanooga residents surveyed, 60 indicated that they participated in a recycling program. In Knoxville, 120 residents were surveyed and 36 claimed to recycle.
a. Determine a 95% confidence interval estimate for the difference between the proportion of residents recycling in the two cities.
b. From your answer in Part a, is there sufficient evidence to conclude that there is a significant difference in the proportion of residents participating in a recycling program?
a. Determine a 95% confidence interval estimate for the difference between the proportion of residents recycling in the two cities.
b. From your answer in Part a, is there sufficient evidence to conclude that there is a significant difference in the proportion of residents participating in a recycling program?

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
56
Exhibit 11-9
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-For a two-tailed test at 98.5% confidence, Z =
A) ± 2.17
B) ± 1.96
C) ± 2.98
D) ± 2.43
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-For a two-tailed test at 98.5% confidence, Z =
A) ± 2.17
B) ± 1.96
C) ± 2.98
D) ± 2.43

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
57
Exhibit 11-9
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-We are interested in testing the following hypotheses. H0: P1- P2 ? 0
Ha: P1- P2 > 0
The test statistic Z is computed to be 0.58. The p-value for this test is
A) 0.7190
B) 0.2810
C) 0.5620
D) 0.5800
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-We are interested in testing the following hypotheses. H0: P1- P2 ? 0
Ha: P1- P2 > 0
The test statistic Z is computed to be 0.58. The p-value for this test is
A) 0.7190
B) 0.2810
C) 0.5620
D) 0.5800

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
58
Exhibit 11-7
The results of a recent poll on the preference of shoppers regarding two products are shown below.
-Refer to Exhibit 11-7. The point estimate for the difference between the two population proportions in favor of this product is
A) 52
B) 100
C) 0.44
D) 0.02
The results of a recent poll on the preference of shoppers regarding two products are shown below.
-Refer to Exhibit 11-7. The point estimate for the difference between the two population proportions in favor of this product is
A) 52
B) 100
C) 0.44
D) 0.02

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
59
Exhibit 11-9
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-Refer to Exhibit 11-9. The standard error of is
A) 0.48
B) 0.50
C) 0.03
D) 0.0243
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-Refer to Exhibit 11-9. The standard error of is
A) 0.48
B) 0.50
C) 0.03
D) 0.0243

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
60
Exhibit 11-9
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-Refer to Exhibit 11-9. The point estimate for the difference between the proportions is
A) -0.02
B) 0.048
C) 100
D) 66
The results of a recent poll on the preference of teenagers regarding the types of music they listen to are shown below.
-Refer to Exhibit 11-9. The point estimate for the difference between the proportions is
A) -0.02
B) 0.048
C) 100
D) 66

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
61
The results of a recent poll on the preference of voters regarding presidential candidates are shown below.
Candidate
Voters Surveyed
Voters Favoring This Candidate
A 400 192
B 450 225
At 95% confidence, test to determine whether or not there is a significant difference between the preferences for the two candidates.
Candidate
Voters Surveyed
Voters Favoring This Candidate
A 400 192
B 450 225
At 95% confidence, test to determine whether or not there is a significant difference between the preferences for the two candidates.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
62
A poll was taken this year asking college students if they considered themselves overweight. A similar poll was taken five years ago. Results are summarized below. Has the proportion increased significantly? Let α = 0.05.
Sample Size Number Considered
Themselves Overweight
Present Sample 300 150
Previous sample 275 121
Sample Size Number Considered
Themselves Overweight
Present Sample 300 150
Previous sample 275 121

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
63
In a sample of 100 Republicans, 60 favored the President's anti-drug program. While in a sample of 150 Democrats, 84 favored his program. At 95% confidence, test to see if there is a significant difference in the proportions of the Democrats and the Republicans who favored the President's anti-drug program.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
64
During the recent primary elections, the democratic presidential candidate showed the following pre-election voter support in Alabama and Mississippi.
State Voters Surveyed
Voters Favoring the Democratic Candidate
Alabama 800 440
Mississippi 600 360
a. We want to determine whether or not the proportions of voters favoring the Democratic candidate were the same in both states. Provide the hypotheses.
b. Compute the test statistic.
c. Determine the p-value; and at 95% confidence, test the above hypotheses.
State Voters Surveyed
Voters Favoring the Democratic Candidate
Alabama 800 440
Mississippi 600 360
a. We want to determine whether or not the proportions of voters favoring the Democratic candidate were the same in both states. Provide the hypotheses.
b. Compute the test statistic.
c. Determine the p-value; and at 95% confidence, test the above hypotheses.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
65
A medical journal reported the following frequencies of deaths due to cardiac arrest for each day of the week:
Cardiac Death by Day of the Week
 We want to determine whether the number of deaths is uniform over the week.
We want to determine whether the number of deaths is uniform over the week.
a. Compute the test statistic.
b. Using the p-value approach at 95% confidence, test for the uniformity of death over the week.
c. Using the critical value approach, perform the test for uniformity.
Cardiac Death by Day of the Week
 We want to determine whether the number of deaths is uniform over the week.
We want to determine whether the number of deaths is uniform over the week. a. Compute the test statistic.
b. Using the p-value approach at 95% confidence, test for the uniformity of death over the week.
c. Using the critical value approach, perform the test for uniformity.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
66
In 2013, forty percent of the students at a major university were Business majors, 35% were Engineering majors and the rest of the students were majoring in other fields. In a sample of 600 students from the same university taken in 2014, two hundred were Business majors, 220 were Engineering majors and the remaining students in the sample were majoring in other fields. At 95% confidence, test to see if there has been a significant change in the proportions between 2013 and 2014.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
67
The results of a recent poll on the preference of voters regarding the presidential candidates are shown below.
Voters Surveyed
Voters Favoring This Candidate
Candidate A 200 150
Candidate B 300 195
a. Develop a 90% confidence interval estimate for the difference between the proportion of voters favoring each candidate.
b. Does your confidence interval provide conclusive evidence that one of the candidates is favored more? Explain.
Voters Surveyed
Voters Favoring This Candidate
Candidate A 200 150
Candidate B 300 195
a. Develop a 90% confidence interval estimate for the difference between the proportion of voters favoring each candidate.
b. Does your confidence interval provide conclusive evidence that one of the candidates is favored more? Explain.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
68
Babies weighing less than 5.5 pounds at birth are considered "lowbirthweight babies." In the United States, 7.6% of newborns are low-birth-weight babies. The following information was accumulated from samples of new births taken from two counties.
a. Develop a 95% confidence interval estimate for the difference between the proportions of low-birth-weight babies in the two counties.
b. Is there conclusive evidence that one of the proportions is significantly more than the other? If yes, which county? Explain, using the results of part a). Do not perform any test.
a. Develop a 95% confidence interval estimate for the difference between the proportions of low-birth-weight babies in the two counties.
b. Is there conclusive evidence that one of the proportions is significantly more than the other? If yes, which county? Explain, using the results of part a). Do not perform any test.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
69
Among 1,000 managers with degrees in business administration, the following data have been accumulated as to their fields of concentration.
We want to determine if the position in management is independent of field major) of concentration.
a. Compute the test statistic.
b. Using the p-value approach at 90% confidence, test to determine if management position is independent of major.
c. Using the critical value approach, test the hypotheses. Let ? = 0.10.
We want to determine if the position in management is independent of field major) of concentration.
a. Compute the test statistic.
b. Using the p-value approach at 90% confidence, test to determine if management position is independent of major.
c. Using the critical value approach, test the hypotheses. Let ? = 0.10.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
70
Before the start of the Winter Olympics, it was expected that the percentages of medals awarded to the top contenders to be as follows.
 Midway through the Olympics, of the 120 medals awarded, the following distribution was observed.
Midway through the Olympics, of the 120 medals awarded, the following distribution was observed.
 We want to test to see if there is a significant difference between the expected and actual awards given.
We want to test to see if there is a significant difference between the expected and actual awards given.
a. Compute the test statistic.
b. Using the p-value approach, test to see if there is a significant difference between the expected and the actual values. Let α = .05.
c. At 95% confidence, test for a significant difference using the critical value approach.
 Midway through the Olympics, of the 120 medals awarded, the following distribution was observed.
Midway through the Olympics, of the 120 medals awarded, the following distribution was observed. We want to test to see if there is a significant difference between the expected and actual awards given.
We want to test to see if there is a significant difference between the expected and actual awards given. a. Compute the test statistic.
b. Using the p-value approach, test to see if there is a significant difference between the expected and the actual values. Let α = .05.
c. At 95% confidence, test for a significant difference using the critical value approach.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
71
From a poll of 800 television viewers, the following data have been accumulated as to their levels of education and their preference of television stations. We are interested in determining if the selection of a TV station is independent of the level of education.
Educational Level
a. State the null and the alternative hypotheses.
b. Show the contingency table of the expected frequencies.
c. Compute the test statistic.
d. The null hypothesis is to be tested at 95% confidence. Determine the critical value for this test.
e. Determine the p-value and perform the test.
Educational Level
a. State the null and the alternative hypotheses.
b. Show the contingency table of the expected frequencies.
c. Compute the test statistic.
d. The null hypothesis is to be tested at 95% confidence. Determine the critical value for this test.
e. Determine the p-value and perform the test.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
72
Before the presidential debates, it was expected that the percentages of registered voters in favor of various candidates would be as follows.
 After the presidential debates, a random sample of 1200 voters showed that 540 favored the Democratic candidate; 480 were in favor of the Republican candidate; 40 were in favor of the Independent candidate, and 140 were undecided. We want to see if the proportion of voters has changed.
After the presidential debates, a random sample of 1200 voters showed that 540 favored the Democratic candidate; 480 were in favor of the Republican candidate; 40 were in favor of the Independent candidate, and 140 were undecided. We want to see if the proportion of voters has changed.
a. Compute the test statistic.
b. Use the p-value approach to test the hypotheses. Let α = .05.
c. Using the critical value approach, test the hypotheses. Let α = .05.
 After the presidential debates, a random sample of 1200 voters showed that 540 favored the Democratic candidate; 480 were in favor of the Republican candidate; 40 were in favor of the Independent candidate, and 140 were undecided. We want to see if the proportion of voters has changed.
After the presidential debates, a random sample of 1200 voters showed that 540 favored the Democratic candidate; 480 were in favor of the Republican candidate; 40 were in favor of the Independent candidate, and 140 were undecided. We want to see if the proportion of voters has changed. a. Compute the test statistic.
b. Use the p-value approach to test the hypotheses. Let α = .05.
c. Using the critical value approach, test the hypotheses. Let α = .05.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
73
In a sample of 40 Democrats, 6 opposed the President's foreign policy, while of 50 Republicans, 8 were opposed to his policy. Determine a 90% confidence interval estimate for the difference between the proportions of the opinions of the individuals in the two parties.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
74
Before the rush began for Christmas shopping, a department store had noted that the percentage of its customers who use the store's credit card, the percentage of those who use a major credit card, and the percentage of those who pay cash are the same. During the Christmas rush in a sample of 150 shoppers, 46 used the store's credit card; 43 used a major credit card; and 61 paid cash. With α = 0.05, test to see if the methods of payment have changed during the Christmas rush.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
75
In the last presidential election, before the candidates started their major campaigns, the percentages of registered voters who favored the various candidates were as follows.
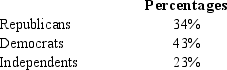 After the major campaigns began, a random sample of 400 voters showed that 172 favored the Republican candidate; 164 were in favor of the Democratic candidate; and 64 favored the Independent candidate. We are interested in determining whether the proportion of voters who favored the various candidates had changed.
After the major campaigns began, a random sample of 400 voters showed that 172 favored the Republican candidate; 164 were in favor of the Democratic candidate; and 64 favored the Independent candidate. We are interested in determining whether the proportion of voters who favored the various candidates had changed.
a. Compute the test statistic.
b. Using the p-value approach, test to see if the proportions have changed.
c. Using the critical value approach, test the hypotheses.
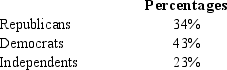 After the major campaigns began, a random sample of 400 voters showed that 172 favored the Republican candidate; 164 were in favor of the Democratic candidate; and 64 favored the Independent candidate. We are interested in determining whether the proportion of voters who favored the various candidates had changed.
After the major campaigns began, a random sample of 400 voters showed that 172 favored the Republican candidate; 164 were in favor of the Democratic candidate; and 64 favored the Independent candidate. We are interested in determining whether the proportion of voters who favored the various candidates had changed. a. Compute the test statistic.
b. Using the p-value approach, test to see if the proportions have changed.
c. Using the critical value approach, test the hypotheses.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
76
The results of a recent study regarding smoking and three types of illness are shown in the following table.
We are interested in determining whether or not illness is independent of smoking.
a. State the null and alternative hypotheses to be tested.
b. Show the contingency table of the expected frequencies.
c. Compute the test statistic.
d. The null hypothesis is to be tested at 95% confidence. Determine the critical value for this test. What do you conclude?
e. Determine the p-value and perform the test.
We are interested in determining whether or not illness is independent of smoking.
a. State the null and alternative hypotheses to be tested.
b. Show the contingency table of the expected frequencies.
c. Compute the test statistic.
d. The null hypothesis is to be tested at 95% confidence. Determine the critical value for this test. What do you conclude?
e. Determine the p-value and perform the test.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
77
The reliability of two types of machines used in the same manufacturing process is to be tested. The first machine failed to operate correctly in 90 out of 300 trials while the second type failed to operate correctly in 50 out of 250 trials.
a. Give a point estimate for the difference between the population proportions of these machines.
b. Calculate the pooled estimate of the population proportion.
c. Carry out a hypothesis test to check whether there is a statistically significant difference in the reliability for the two types of machines using a .10 level of significance.
a. Give a point estimate for the difference between the population proportions of these machines.
b. Calculate the pooled estimate of the population proportion.
c. Carry out a hypothesis test to check whether there is a statistically significant difference in the reliability for the two types of machines using a .10 level of significance.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
78
Last school year, in the school of Business Administration, 30% were Accounting majors, 24% Management majors, 26% Marketing majors, and 20% Economics majors. A sample of 300 students taken from this year's students of the school showed the following number of students in each major:
 We want to see if there has been a significant change in the number of students in each major.
We want to see if there has been a significant change in the number of students in each major.
a. Compute the test statistic.
b. Has there been any significant change in the number of students in each major between the last school year and this school year. Use the p-value approach and let α = .05.
 We want to see if there has been a significant change in the number of students in each major.
We want to see if there has been a significant change in the number of students in each major. a. Compute the test statistic.
b. Has there been any significant change in the number of students in each major between the last school year and this school year. Use the p-value approach and let α = .05.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
79
In a random sample of 200 Republicans, 160 opposed the new tax laws. While in a sample of 120 Democrats, 84 opposed the new tax laws. Determine a 95% confidence interval estimate for the difference between the proportions of Republicans and Democrats opposed to this new law.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
80
From production line A, a sample of 500 items is selected at random, and it is determined that 30 items are defective. In a sample of 300 items from production process B which produces identical items to line A), there are 12 defective items. Determine a 95% confidence interval estimate for the difference between the proportion of defectives in the two lines.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck


