Deck 4: Basic Estimation Techniques

Question 1

In a linear regression equation of the form Y = a + bX, the intercept parameter a shows

A) the value of X when Y is zero.
B) the value of Y when X is zero.
C) the amount that Y changes when X changes by one unit.
D) the amount that X changes when Y changes by one unit.

Answer 1

the value of Y when X is zero.

Question 2

The linear regression equation, Y = a + bX, was estimated. The following computer printout was
obtained:
$\begin{array}{rllll}\text { DEPENDENT VARIABLE: } & \text { Y } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ON F } \\\text { OBSERVATIONS: } &18 & 0.3066 & 7.076 & 0.0171\end{array}$

$\begin{array}{lllll}\text { VARIABLE } & \begin{array}{llll}\text { PARAMETER } \\\text { ESTIMATE }\end{array} & \begin{array}{l}\text { STANDARD } \\\text { ERROR }\end{array} & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & 15.48 & 5.09 & 3.04 & 0.0008\\X&-21.36&8.03&-2.66&0.0171\end{array}$

-Which of the following statements is correct at the 1% level of significance?

A) Both $\hat { a }$ and
$\hat { b }$ are statistically significant.
B) Neither $\hat { a }$ nor
$\hat { b }$ is statistically significant.
C) $\hat { a }$ is statistically significant, but
$\hat { b }$ is not.
D) $\hat { b }$ is statistically significant, but
$\hat { a }$ is not.

Answer 2

$\hat { a }$ is statistically significant, but
$\hat { b }$ is not.

Question 3

In a linear regression equation Y = a + bX, the fitted or predicted value of Y is

A) the value of Y obtained by substituting specific values of X into the sample regression equation.
B) the value of X associated with a particular value of Y.
C) the value of X that the regression equation predicts.
D) the values of the parameters predicted by the estimators.
E) the value of Y associated with a particular value of X in the sample.

Answer 3

the value of Y obtained by substituting specific values of X into the sample regression equation.

Question 4

The sample regression line

A) shows the actual (or true) relation between the dependent and independent variables.
B) is used to estimate the population regression line.
C) connects the data points in a sample.
D) is estimated by the population regression line.
E) maximizes the sum of the squared differences between the data points in a sample and the sample regression line.

Question 5

The linear regression equation, Y = a + bX, was estimated. The following computer printout was
obtained:
$\begin{array}{rllll}\text { DEPENDENT VARIABLE: } & \text { Y } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ON F } \\\text { OBSERVATIONS: } &18 & 0.3066 & 7.076 & 0.0171\end{array}$

$\begin{array}{lllll}\text { VARIABLE } & \begin{array}{llll}\text { PARAMETER } \\\text { ESTIMATE }\end{array} & \begin{array}{l}\text { STANDARD } \\\text { ERROR }\end{array} & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & 15.48 & 5.09 & 3.04 & 0.0008\\X&-21.36&8.03&-2.66&0.0171\end{array}$

-If X equals 20, what is the predicted value of Y?

A) 186.42
B) 165.69
C) -186.42
D) -411.72

Question 6

The critical value of t is the value that a t-statistic must exceed in order to

A) reject the hypothesis that the true value of a parameter equals zero.
B) accept the hypothesis that the estimated value of parameter equals the true value.
C) reject the hypothesis that the estimated value of the parameter equals the true value.
D) reject the hypothesis that the estimated value of the parameter exceeds the true value.

Question 7

The linear regression equation, Y = a + bX, was estimated. The following computer printout was
obtained:
$\begin{array}{rllll}\text { DEPENDENT VARIABLE: } & \text { Y } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ON F } \\\text { OBSERVATIONS: } &18 & 0.3066 & 7.076 & 0.0171\end{array}$

$\begin{array}{lllll}\text { VARIABLE } & \begin{array}{llll}\text { PARAMETER } \\\text { ESTIMATE }\end{array} & \begin{array}{l}\text { STANDARD } \\\text { ERROR }\end{array} & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & 15.48 & 5.09 & 3.04 & 0.0008\\X&-21.36&8.03&-2.66&0.0171\end{array}$

-The exact level of significance of $\hat { b }$ is

A) 0.171 percent.
B) 1 percent.
C) 1.71 percent.
D) 2.66 percent.
E) 2.921 percent.

Question 8

The linear regression equation, Y = a + bX, was estimated. The following computer printout was
obtained:
$\begin{array}{rllll}\text { DEPENDENT VARIABLE: } & \text { Y } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ON F } \\\text { OBSERVATIONS: } &18 & 0.3066 & 7.076 & 0.0171\end{array}$

$\begin{array}{lllll}\text { VARIABLE } & \begin{array}{llll}\text { PARAMETER } \\\text { ESTIMATE }\end{array} & \begin{array}{l}\text { STANDARD } \\\text { ERROR }\end{array} & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & 15.48 & 5.09 & 3.04 & 0.0008\\X&-21.36&8.03&-2.66&0.0171\end{array}$

-What is the critical value of t at the 1% level of significance?

A) 1.746
B) 2.120
C) 2.878
D) 2.921

Question 9

A parameter estimate is said to be statistically significant if there is sufficient evidence that the

A) sample regression equals the population regression.
B) parameter estimated from the sample equals the true value of the parameter.
C) value of the t-ratio equals the critical value.
D) true value of the parameter does not equal zero.

Question 10

The method of least squares

A) can be used to estimate the explanatory variables in a linear regression equation.
B) can be used to estimate the slope parameters of a linear equation.
C) minimizes the distance between the population regression line and the sample regression line.
D) all of the above

Question 11

The linear regression equation, Y = a + bX, was estimated. The following computer printout was
obtained:
$\begin{array}{rllll}\text { DEPENDENT VARIABLE: } & \text { Y } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ON F } \\\text { OBSERVATIONS: } &18 & 0.3066 & 7.076 & 0.0171\end{array}$

$\begin{array}{lllll}\text { VARIABLE } & \begin{array}{llll}\text { PARAMETER } \\\text { ESTIMATE }\end{array} & \begin{array}{l}\text { STANDARD } \\\text { ERROR }\end{array} & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & 15.48 & 5.09 & 3.04 & 0.0008\\X&-21.36&8.03&-2.66&0.0171\end{array}$

-The value of the R² statistic indicates that

A) 0.3066% of the total variation in Y is explained by the regression equation.
B) 0.3066% of the total variation in X is explained by the regression equation.
C) 30.66% of the total variation in Y is explained by the regression equation.
D) 30.66% of the total variation in X is explained by the regression equation.

Question 12

In the linear model $Y = a + b X + c Z$ , a test of the hypothesis that parameter c equals zero is

A) an F-test.
B) an R²-test.
C) a zero-statistic.
D) a t-test.
E) a Z-test.

Question 13

In a regression equation, the ______ captures the effects of factors that might influence the dependent variable but aren't used as explanatory variables.

A) intercept
B) slope parameter
C) R-square
D) random error term

Question 14

Which of the following is an example of a time-series data set?

A) amount of labor employed in each factory in the U.S. in 2010.
B) amount of labor employed yearly in a specific factory from 1990 through 2010.
C) average amount of labor employed at specific times of the day at a specific factory in 2010.
D) All of the above are time-series data sets.

Question 15

An estimator is unbiased if it produces

A) a parameter from the sample that equals the true parameter.
B) estimates of a parameter that are close to the true parameter.
C) estimates of a parameter that are statistically significant.
D) estimates of a parameter that are on average equal to the true parameter.
E) both b and c

Question 16

In a linear regression equation of the form Y = a + bX, the slope parameter b shows

A) $\Delta$ X / $\Delta$ Y.
B) $\Delta$ Y / $\Delta$ X.
C) $\Delta$ Y / $\Delta$ b.
D) $\Delta$ X / $\Delta$ b.
E) none of the above

Question 17

The linear regression equation, Y = a + bX, was estimated. The following computer printout was
obtained:
$\begin{array}{rllll}\text { DEPENDENT VARIABLE: } & \text { Y } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ON F } \\\text { OBSERVATIONS: } &18 & 0.3066 & 7.076 & 0.0171\end{array}$

$\begin{array}{lllll}\text { VARIABLE } & \begin{array}{llll}\text { PARAMETER } \\\text { ESTIMATE }\end{array} & \begin{array}{l}\text { STANDARD } \\\text { ERROR }\end{array} & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & 15.48 & 5.09 & 3.04 & 0.0008\\X&-21.36&8.03&-2.66&0.0171\end{array}$

-The parameter estimate of b indicates

A) X increases by 8.03 units when Y increases by one unit.
B) X decreases by 21.36 units when Y increases by one unit.
C) Y decreases by 2.66 units when X increases by one unit.
D) a 10-unit decrease in X results in a 213.6 unit increase in Y.

Question 18

To test whether the overall regression equation is statistically significant one uses

A) the t-statistic.
B) the R²-statistic.
C) the F-statistic.
D) the standard error statistic.

Question 19

If an analyst believes that more than one explanatory variable explains the variation in the dependent variable, what model should be used?

A) a simple linear regression model
B) a multiple regression model
C) a nonlinear regression model
D) a log-linear model

Question 20

The linear regression equation, Y = a + bX, was estimated. The following computer printout was
obtained:
$\begin{array}{rllll}\text { DEPENDENT VARIABLE: } & \text { Y } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ON F } \\\text { OBSERVATIONS: } &18 & 0.3066 & 7.076 & 0.0171\end{array}$

$\begin{array}{lllll}\text { VARIABLE } & \begin{array}{llll}\text { PARAMETER } \\\text { ESTIMATE }\end{array} & \begin{array}{l}\text { STANDARD } \\\text { ERROR }\end{array} & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & 15.48 & 5.09 & 3.04 & 0.0008\\X&-21.36&8.03&-2.66&0.0171\end{array}$

-The parameter estimate of a indicates

A) when X is zero, Y is 5.09.
B) when X is zero, Y is 15.48.
C) when Y is zero, X is -21.36.
D) when Y is zero, X is 8.03.

Question 21

Suppose you are testing the statistical significance (at the 1% significance level) of a parameter estimate from the estimated regression model: M = a + bR + cI
Which is estimated using a cross-section data set on 22 firms. The critical value of the appropriate test statistic is

A) t_critical = 2.861.
B) t_critical = -.845.
C) t_critical = 2.845.
D) F_critical = 5.93.
E) F_critical = 19.44.

Question 22

A firm is experiencing theft problems at its warehouse. A consultant to the firm believes that the dollar loss from theft each week (T) depends on the number of security guards (G) and on the unemployment rate in the county where the warehouse is located (U measured as a percent). In order to test this hypothesis, the consultant estimated the regression equation T = a + bG + cU and obtained the following results:
$$\begin{array} { c l l l l l } \text { DEPENDENT VARIAELE: } & \text { T } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & 27 & \mathbf { 0 . 7 7 9 3 } & 42.38 & \mathbf { 0 . 0 0 0 1 } & \\& & \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & & \text { ESTMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & & 5150.43 & 1740.72 & \mathbf { 2 . 9 6 } & \mathbf { 0 . 0 0 6 8 } \\\text { G } & & - 480.92 & 130.65 & - \mathbf { 3 . 6 8 } & \mathbf { 0 . 0 0 1 2 } \\\text { U } & & 211.0 & 75.0 & \mathbf { 2 . 8 1 } & \mathbf { 0 . 0 0 9 5 }\end{array}$$

-If the firm hires 6 guards and the unemployment rate in the county is 10% (U = 10), what is the predicted dollar loss to theft per week?

A) $4,375 per week
B) $5,150 per week
C) $8,300 per week
D) $9,955 per week

Question 23

A firm is experiencing theft problems at its warehouse. A consultant to the firm believes that the dollar loss from theft each week (T) depends on the number of security guards (G) and on the unemployment rate in the county where the warehouse is located (U measured as a percent). In order to test this hypothesis, the consultant estimated the regression equation T = a + bG + cU and obtained the following results:
$$\begin{array} { c l l l l l } \text { DEPENDENT VARIAELE: } & \text { T } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & 27 & \mathbf { 0 . 7 7 9 3 } & 42.38 & \mathbf { 0 . 0 0 0 1 } & \\& & \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & & \text { ESTMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & & 5150.43 & 1740.72 & \mathbf { 2 . 9 6 } & \mathbf { 0 . 0 0 6 8 } \\\text { G } & & - 480.92 & 130.65 & - \mathbf { 3 . 6 8 } & \mathbf { 0 . 0 0 1 2 } \\\text { U } & & 211.0 & 75.0 & \mathbf { 2 . 8 1 } & \mathbf { 0 . 0 0 9 5 }\end{array}$$

-Which of the following is correct at the 1% level of significance?

A) The regression equation as a whole is statistically significant because the p-value of F is smaller than 0.01.
B) The estimates of the parameters a, b, and c are all statistically significant because the absolute values of their t-ratios exceed 2.797.
C) The estimates of the parameters a, b, and c are all statistically significant because the p- values for, $\hat { a }$ , $\hat { b }$ and $\hat { c }$ are all less than 0.01.
D) The critical value of t is 2.797.
E) all of the above

Question 24

If the p-value is 10%, then the

A) level of significance is 10%.
B) level of confidence is 90%.
C) probability of a Type I error is 90%.
D) both a and b
E) all of the above

Question 25

Refer to the following nonlinear model which relates W to P, Q, and R:
$W = a P ^ { b } Q ^ { c } R ^ { d }$
The computer output form the regression analysis is:
$$\begin{array} { r l l l l l } \text { DEPENDENTVARIAELE: } & \text { LNW } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 19 } & \mathbf { 0 . 9 0 2 3 } & 43.12 & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & \mathbf { 2 . 5 0 } & \mathbf { 0 . 4 5 } & \mathbf { 5 . 5 6 } & \mathbf { 0 . 0 0 0 1 } \\\text { LNP } & - 5.10 & 1.75 & - \mathbf { 2 . 9 1 } & \mathbf { 0 . 0 1 1 3 } \\\text { LNQ } & 12.4 & \mathbf { 3 . 2 } & \mathbf { 3 . 8 3 } & \mathbf { 0 . 0 0 1 7 } \\\text { LNR } & \mathbf { - 6 . 0 0 } & 1.5 & - 400 & \mathbf { 0 . 0 0 1 0 }\end{array}$$

-The estimated value of a is

A) 0.916
B) 12.182
C) 2.50
D) 2.66

Question 26

Suppose you are testing the statistical significance (at the 5% significance level) of a parameter estimate from the estimated regression equation: Y = a + bR + cS + dW
Which is estimated using a time-series sample containing monthly observations over a 30-month time period. The critical value of the appropriate test statistic is

A) t_critical = 2.042.
B) t_critical = 2.056.
C) F_critical = 4.22.
D) F_critical = 7.76.

Question 27

Refer to the following computer output from estimating the parameters of the nonlinear model
$$\begin{array} { r l l l l l } \text { DEPENDENT VARIAELE: } & \text { LNY } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 32 } & \mathbf { 0 . 7 7 5 6 } & \mathbf { 3 2 . 4 4 } & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTEREEPT } & \mathbf { - 0 . 5 9 3 1 } & \mathbf { 0 . 3 2 } & \mathbf { - 2 . 1 7 } & \mathbf { 0 . 0 3 9 0 } \\\text { LNRR } & \mathbf { 4 . 6 5 } & 1.36 & \mathbf { 3 . 4 3 } & \mathbf { 0 . 0 0 1 9 } \\\text { LNS } & \mathbf { - 0 . 4 4 } & \mathbf { 0 . 2 4 } & - 1.83 & \mathbf { 0 . 0 7 7 4 } \\\text { LNT } & \mathbf { 8 . 2 8 } & \mathbf { 4 . 6 } & \mathbf { 1 . 8 0 } & \mathbf { 0 . 0 8 2 6 }\end{array}$$

-The nonlinear relation can be transformed into the following linear regression model:

A) $Y = \ln \left( a R ^ { b } S ^ { c } T ^ { d } \right)$
B) $\ln Y = \ln \left( a R ^ { \mathrm { b } } S ^ { \mathrm { c } } T ^ { \mathrm { d } } \right)$
C) $\ln Y = \ln a \cdot \ln R \cdot \ln S \cdot \ln T$
D) $\ln Y = \ln a + b \ln R + c \ln S + d \ln T$

Question 28

Refer to the following nonlinear model which relates W to P, Q, and R:
$W = a P ^ { b } Q ^ { c } R ^ { d }$
The computer output form the regression analysis is:
$$\begin{array} { r l l l l l } \text { DEPENDENTVARIAELE: } & \text { LNW } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 19 } & \mathbf { 0 . 9 0 2 3 } & 43.12 & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & \mathbf { 2 . 5 0 } & \mathbf { 0 . 4 5 } & \mathbf { 5 . 5 6 } & \mathbf { 0 . 0 0 0 1 } \\\text { LNP } & - 5.10 & 1.75 & - \mathbf { 2 . 9 1 } & \mathbf { 0 . 0 1 1 3 } \\\text { LNQ } & 12.4 & \mathbf { 3 . 2 } & \mathbf { 3 . 8 3 } & \mathbf { 0 . 0 0 1 7 } \\\text { LNR } & \mathbf { - 6 . 0 0 } & 1.5 & - 400 & \mathbf { 0 . 0 0 1 0 }\end{array}$$

-If R decreases by 12% (all other things constant), W will

A) decrease by 72%.
B) decrease by 6%.
C) increase by 6%.
D) increase by 72%.

Question 29

Refer to the following computer output from estimating the parameters of the nonlinear model
$$\begin{array} { r l l l l l } \text { DEPENDENT VARIAELE: } & \text { LNY } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 32 } & \mathbf { 0 . 7 7 5 6 } & \mathbf { 3 2 . 4 4 } & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTEREEPT } & \mathbf { - 0 . 5 9 3 1 } & \mathbf { 0 . 3 2 } & \mathbf { - 2 . 1 7 } & \mathbf { 0 . 0 3 9 0 } \\\text { LNRR } & \mathbf { 4 . 6 5 } & 1.36 & \mathbf { 3 . 4 3 } & \mathbf { 0 . 0 0 1 9 } \\\text { LNS } & \mathbf { - 0 . 4 4 } & \mathbf { 0 . 2 4 } & - 1.83 & \mathbf { 0 . 0 7 7 4 } \\\text { LNT } & \mathbf { 8 . 2 8 } & \mathbf { 4 . 6 } & \mathbf { 1 . 8 0 } & \mathbf { 0 . 0 8 2 6 }\end{array}$$

-The estimated value of a is

A) -0.6931
B) 0.50
C) -3.67
D) 2.66

Question 30

In the nonlinear function $Y = a X ^ { b } Z ^ { 2 }$ , the parameter c measures

A) If $\Delta$ Y / $\Delta$ Z.
B) the percent change in Y for a 1 percent change in Z.
C) the elasticity of Y with respect to Z.
D) both a and c
E) both b and c

Question 31

A firm is experiencing theft problems at its warehouse. A consultant to the firm believes that the dollar loss from theft each week (T) depends on the number of security guards (G) and on the unemployment rate in the county where the warehouse is located (U measured as a percent). In order to test this hypothesis, the consultant estimated the regression equation T = a + bG + cU and obtained the following results:
$$\begin{array} { c l l l l l } \text { DEPENDENT VARIAELE: } & \text { T } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & 27 & \mathbf { 0 . 7 7 9 3 } & 42.38 & \mathbf { 0 . 0 0 0 1 } & \\& & \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & & \text { ESTMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & & 5150.43 & 1740.72 & \mathbf { 2 . 9 6 } & \mathbf { 0 . 0 0 6 8 } \\\text { G } & & - 480.92 & 130.65 & - \mathbf { 3 . 6 8 } & \mathbf { 0 . 0 0 1 2 } \\\text { U } & & 211.0 & 75.0 & \mathbf { 2 . 8 1 } & \mathbf { 0 . 0 0 9 5 }\end{array}$$

-Hiring one more guard per week will decrease the losses due to theft at the warehouse by _________ per week.

A) $5,150
B) $211
C) $130
D) $480.92

Question 32

Refer to the following computer output from estimating the parameters of the nonlinear model
$$\begin{array} { r l l l l l } \text { DEPENDENT VARIAELE: } & \text { LNY } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 32 } & \mathbf { 0 . 7 7 5 6 } & \mathbf { 3 2 . 4 4 } & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTEREEPT } & \mathbf { - 0 . 5 9 3 1 } & \mathbf { 0 . 3 2 } & \mathbf { - 2 . 1 7 } & \mathbf { 0 . 0 3 9 0 } \\\text { LNRR } & \mathbf { 4 . 6 5 } & 1.36 & \mathbf { 3 . 4 3 } & \mathbf { 0 . 0 0 1 9 } \\\text { LNS } & \mathbf { - 0 . 4 4 } & \mathbf { 0 . 2 4 } & - 1.83 & \mathbf { 0 . 0 7 7 4 } \\\text { LNT } & \mathbf { 8 . 2 8 } & \mathbf { 4 . 6 } & \mathbf { 1 . 8 0 } & \mathbf { 0 . 0 8 2 6 }\end{array}$$

-Which of the parameter estimates are statistically significant at the 90% level of confidence?

A) All the parameter estimates are statistically significant.
B) All parameter estimates except $\hat { a }$ and
$\hat { b }$ are statistically significant.
C) $\hat { a }$ is not statistically significant, but all the rest of the parameter estimates are significant.
D) $\hat { c }$ is not statistically significant, but all the rest of the parameter estimates are significant.

Question 33

Refer to the following nonlinear model which relates W to P, Q, and R:
$W = a P ^ { b } Q ^ { c } R ^ { d }$
The computer output form the regression analysis is:
$$\begin{array} { r l l l l l } \text { DEPENDENTVARIAELE: } & \text { LNW } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 19 } & \mathbf { 0 . 9 0 2 3 } & 43.12 & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & \mathbf { 2 . 5 0 } & \mathbf { 0 . 4 5 } & \mathbf { 5 . 5 6 } & \mathbf { 0 . 0 0 0 1 } \\\text { LNP } & - 5.10 & 1.75 & - \mathbf { 2 . 9 1 } & \mathbf { 0 . 0 1 1 3 } \\\text { LNQ } & 12.4 & \mathbf { 3 . 2 } & \mathbf { 3 . 8 3 } & \mathbf { 0 . 0 0 1 7 } \\\text { LNR } & \mathbf { - 6 . 0 0 } & 1.5 & - 400 & \mathbf { 0 . 0 0 1 0 }\end{array}$$

-The nonlinear relation can be transformed into the following linear regression model:

A) $W = \ln \left( a P ^ { b } Q ^ { c } R ^ { \mathrm { h } } \right)$
B) $\ln W = \ln \left( a P ^ { \mathrm { b } } Q ^ { \mathrm { c } } R ^ { \mathrm { d } } \right)$
C) $\ln W = \ln a \cdot \ln P \cdot \ln Q \cdot \ln R$
D) $\ln W = \ln a + b \ln P + c \ln Q + d \ln R$

Question 34

A firm is experiencing theft problems at its warehouse. A consultant to the firm believes that the dollar loss from theft each week (T) depends on the number of security guards (G) and on the unemployment rate in the county where the warehouse is located (U measured as a percent). In order to test this hypothesis, the consultant estimated the regression equation T = a + bG + cU and obtained the following results:
$$\begin{array} { c l l l l l } \text { DEPENDENT VARIAELE: } & \text { T } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & 27 & \mathbf { 0 . 7 7 9 3 } & 42.38 & \mathbf { 0 . 0 0 0 1 } & \\& & \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & & \text { ESTMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & & 5150.43 & 1740.72 & \mathbf { 2 . 9 6 } & \mathbf { 0 . 0 0 6 8 } \\\text { G } & & - 480.92 & 130.65 & - \mathbf { 3 . 6 8 } & \mathbf { 0 . 0 0 1 2 } \\\text { U } & & 211.0 & 75.0 & \mathbf { 2 . 8 1 } & \mathbf { 0 . 0 0 9 5 }\end{array}$$

-Aone percent increase in the level of unemployment in the county results in an increase in losses due to theft of __________ more losses per week.

A) $75
B) $211
C) $280
D) $460

Question 35

Refer to the following computer output from estimating the parameters of the nonlinear model
$$\begin{array} { r l l l l l } \text { DEPENDENT VARIAELE: } & \text { LNY } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 32 } & \mathbf { 0 . 7 7 5 6 } & \mathbf { 3 2 . 4 4 } & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTEREEPT } & \mathbf { - 0 . 5 9 3 1 } & \mathbf { 0 . 3 2 } & \mathbf { - 2 . 1 7 } & \mathbf { 0 . 0 3 9 0 } \\\text { LNRR } & \mathbf { 4 . 6 5 } & 1.36 & \mathbf { 3 . 4 3 } & \mathbf { 0 . 0 0 1 9 } \\\text { LNS } & \mathbf { - 0 . 4 4 } & \mathbf { 0 . 2 4 } & - 1.83 & \mathbf { 0 . 0 7 7 4 } \\\text { LNT } & \mathbf { 8 . 2 8 } & \mathbf { 4 . 6 } & \mathbf { 1 . 8 0 } & \mathbf { 0 . 0 8 2 6 }\end{array}$$

-If R = 1, S = 2, and T = 3, what value do you expect Y will have?

A) 143
B) 1,345
C) 3,289
D) 6,578
E) -4,559

Question 36

Tests for statistical significance must be performed

A) because the TRUE values of the intercept and slope parameters are random variables.
B) because the ESTIMATED values of the intercept and slope parameters are not, in general, equal to the true values of the intercept and slope parameters.
C) because the computed t-ratios are random variables and may be too large to provide evidence that b is not equal to zero.
D) in order to determine whether or not the parameter estimates are far enough away from zero to conclude that the true parameter values are not equal to zero.
E) both b and d

Question 37

Refer to the following nonlinear model which relates W to P, Q, and R:
$W = a P ^ { b } Q ^ { c } R ^ { d }$
The computer output form the regression analysis is:
$$\begin{array} { r l l l l l } \text { DEPENDENTVARIAELE: } & \text { LNW } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 19 } & \mathbf { 0 . 9 0 2 3 } & 43.12 & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & \mathbf { 2 . 5 0 } & \mathbf { 0 . 4 5 } & \mathbf { 5 . 5 6 } & \mathbf { 0 . 0 0 0 1 } \\\text { LNP } & - 5.10 & 1.75 & - \mathbf { 2 . 9 1 } & \mathbf { 0 . 0 1 1 3 } \\\text { LNQ } & 12.4 & \mathbf { 3 . 2 } & \mathbf { 3 . 8 3 } & \mathbf { 0 . 0 0 1 7 } \\\text { LNR } & \mathbf { - 6 . 0 0 } & 1.5 & - 400 & \mathbf { 0 . 0 0 1 0 }\end{array}$$

-Which of the parameter estimates are statistically significant at the 5% level of significance?

A) All the parameter estimates are statistically significant.
B) All parameter estimates except $\hat { a }$ and
$\hat { b }$ are statistically significant.
C) $\hat { a }$ is not statistically significant, but all the rest of the parameter estimates are significant.
D) $\hat {c}$ is not statistically significant, but all the rest of the parameter estimates are significant.

Question 38

Refer to the following computer output from estimating the parameters of the nonlinear model
$$\begin{array} { r l l l l l } \text { DEPENDENT VARIAELE: } & \text { LNY } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 32 } & \mathbf { 0 . 7 7 5 6 } & \mathbf { 3 2 . 4 4 } & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTEREEPT } & \mathbf { - 0 . 5 9 3 1 } & \mathbf { 0 . 3 2 } & \mathbf { - 2 . 1 7 } & \mathbf { 0 . 0 3 9 0 } \\\text { LNRR } & \mathbf { 4 . 6 5 } & 1.36 & \mathbf { 3 . 4 3 } & \mathbf { 0 . 0 0 1 9 } \\\text { LNS } & \mathbf { - 0 . 4 4 } & \mathbf { 0 . 2 4 } & - 1.83 & \mathbf { 0 . 0 7 7 4 } \\\text { LNT } & \mathbf { 8 . 2 8 } & \mathbf { 4 . 6 } & \mathbf { 1 . 8 0 } & \mathbf { 0 . 0 8 2 6 }\end{array}$$

-If S increases by 8% (all other things constant), Y will

A) decrease by 3.52%.
B) decrease by 0.44%.
C) decrease by 4.4%.
D) increase by 0.44%.
E) decrease by 2.4%.

Question 39

Refer to the following nonlinear model which relates W to P, Q, and R:
$W = a P ^ { b } Q ^ { c } R ^ { d }$
The computer output form the regression analysis is:
$$\begin{array} { r l l l l l } \text { DEPENDENTVARIAELE: } & \text { LNW } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 19 } & \mathbf { 0 . 9 0 2 3 } & 43.12 & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & \mathbf { 2 . 5 0 } & \mathbf { 0 . 4 5 } & \mathbf { 5 . 5 6 } & \mathbf { 0 . 0 0 0 1 } \\\text { LNP } & - 5.10 & 1.75 & - \mathbf { 2 . 9 1 } & \mathbf { 0 . 0 1 1 3 } \\\text { LNQ } & 12.4 & \mathbf { 3 . 2 } & \mathbf { 3 . 8 3 } & \mathbf { 0 . 0 0 1 7 } \\\text { LNR } & \mathbf { - 6 . 0 0 } & 1.5 & - 400 & \mathbf { 0 . 0 0 1 0 }\end{array}$$

-If P = 0.5, Q = 1.5, and R = 0.8, what value do you expect W will have?

A) 16,712
B) 243,200
C) 1,345
D) 3,289

Question 40

Refer to the following computer output from estimating the parameters of the nonlinear model
$$\begin{array} { r l l l l l } \text { DEPENDENT VARIAELE: } & \text { LNY } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 32 } & \mathbf { 0 . 7 7 5 6 } & \mathbf { 3 2 . 4 4 } & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTEREEPT } & \mathbf { - 0 . 5 9 3 1 } & \mathbf { 0 . 3 2 } & \mathbf { - 2 . 1 7 } & \mathbf { 0 . 0 3 9 0 } \\\text { LNRR } & \mathbf { 4 . 6 5 } & 1.36 & \mathbf { 3 . 4 3 } & \mathbf { 0 . 0 0 1 9 } \\\text { LNS } & \mathbf { - 0 . 4 4 } & \mathbf { 0 . 2 4 } & - 1.83 & \mathbf { 0 . 0 7 7 4 } \\\text { LNT } & \mathbf { 8 . 2 8 } & \mathbf { 4 . 6 } & \mathbf { 1 . 8 0 } & \mathbf { 0 . 0 8 2 6 }\end{array}$$

-If R decreases by 10% (all other things constant), Y will

A) increase by 4.66%.
B) increase by 46.6%.
C) decrease by 4.66%.
D) decrease by 46.6%.

Question 41

The linear regression equation G = a + bD is estimated using 24 observations on R and W. The least-squares estimate of b is -22.5, and the standard error of the estimate is 8.36. Perform a t-test for statistical significance of $\hat { b }$ at the 1% level of significance.
a. There are _____ degrees of freedom for the t-test.
b. The value of the t-statistic is _________. The critical t-value for the test is _________.
c. The parameter estimate
$\hat { b }$ _________ (is, is not) statistically significant at the 1% level.

Question 42

Refer to the following nonlinear model which relates W to P, Q, and R:
$W = a P ^ { b } Q ^ { c } R ^ { d }$
The computer output form the regression analysis is:
$$\begin{array} { r l l l l l } \text { DEPENDENTVARIAELE: } & \text { LNW } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 19 } & \mathbf { 0 . 9 0 2 3 } & 43.12 & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & \mathbf { 2 . 5 0 } & \mathbf { 0 . 4 5 } & \mathbf { 5 . 5 6 } & \mathbf { 0 . 0 0 0 1 } \\\text { LNP } & - 5.10 & 1.75 & - \mathbf { 2 . 9 1 } & \mathbf { 0 . 0 1 1 3 } \\\text { LNQ } & 12.4 & \mathbf { 3 . 2 } & \mathbf { 3 . 8 3 } & \mathbf { 0 . 0 0 1 7 } \\\text { LNR } & \mathbf { - 6 . 0 0 } & 1.5 & - 400 & \mathbf { 0 . 0 0 1 0 }\end{array}$$

-If P = Q = R = 1, what value do you expect W will have?

A) 0
B) 1
C) 12.182
D) 2.50

Question 43

A simple linear regression equation relates G and D as follows:
G = a + bD
a. The explanatory variable is _______, and the dependent variable is ________.
b. The slope parameter is ______, and the intercept parameter _______.
c. When D is zero, G equals _______.
d. For each one-unit increase in D, the change in R is ______ units.

Question 44

A manager wishes to estimate an average cost equation of the following form:

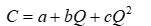
where Q is the level of output. Letting Z = Q² and using least-squares estimation, the manager obtains the following computer output:

$$\begin{array} { | c l l l l l | } \hline \text { DEPENDENT VARIABLE: } & \text { C } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ON F } \\\text { OBSERVATIONS: } & 28 & 0.7679 & 26.47 & 0.0001 & \\ \text { VARIABLE } & \begin{array} { l } \text { PARAMETER } \\\text { ESTIMATE }\end{array} & \begin{array} { l } \text { STANDARD } \\\text { ERROR }\end{array}& \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT }& 200 & 38.00 & 5.26 & 0.0001 \\\text { Q } & - 12.00 & 4.36 & - 2.75 & 0.0111 \\ \text { Z } & 0.50 & 0.16 & 3.13 & 0.0046 \\\hline\end{array}$$

-When output is 40 units, what is average cost?

A) $200
B) $280
C) $360
D) $480
E) $520

Question 45

In a multiple regression model, the coefficients on the independent variables measure

A) the percent of the variation in the dependent variable explained by a change in that independent variable, all other influences held constant.
B) the change in the dependent variable from a one-unit change in that independent variable, all other influences held constant.
C) the change in that independent variable from a one-unit change in the dependent variable, all other influences held constant.
D) the change in the dependent variable explained by the random error, all other influences held constant.

Question 46

The quadratic equation Y = a + bX +cX² can be estimated using linear regression by estimating

A) Y = a + bX + ZX where Z = c²
B) Y = a + ZX where Z = (b + c)
C) Y = a + bZ where Z = X²
D) Y = a + ZX where Z = (b + c)²
E) none of the above will work

Question 47

A manager wishes to estimate an average cost equation of the following form:

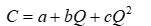
where Q is the level of output. Letting Z = Q² and using least-squares estimation, the manager obtains the following computer output:

$$\begin{array} { | c l l l l l | } \hline \text { DEPENDENT VARIABLE: } & \text { C } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ON F } \\\text { OBSERVATIONS: } & 28 & 0.7679 & 26.47 & 0.0001 & \\ \text { VARIABLE } & \begin{array} { l } \text { PARAMETER } \\\text { ESTIMATE }\end{array} & \begin{array} { l } \text { STANDARD } \\\text { ERROR }\end{array}& \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT }& 200 & 38.00 & 5.26 & 0.0001 \\\text { Q } & - 12.00 & 4.36 & - 2.75 & 0.0111 \\ \text { Z } & 0.50 & 0.16 & 3.13 & 0.0046 \\\hline\end{array}$$

-The value of R² indicates that _______ of the total variation in C is explained by the regression equation.

A) 0.7679%
B) 76.79%
C) 7.679%
D) 7679%

Question 48

A manager wishes to estimate an average cost equation of the following form:

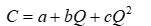
where Q is the level of output. Letting Z = Q² and using least-squares estimation, the manager obtains the following computer output:

$$\begin{array} { | c l l l l l | } \hline \text { DEPENDENT VARIABLE: } & \text { C } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ON F } \\\text { OBSERVATIONS: } & 28 & 0.7679 & 26.47 & 0.0001 & \\ \text { VARIABLE } & \begin{array} { l } \text { PARAMETER } \\\text { ESTIMATE }\end{array} & \begin{array} { l } \text { STANDARD } \\\text { ERROR }\end{array}& \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT }& 200 & 38.00 & 5.26 & 0.0001 \\\text { Q } & - 12.00 & 4.36 & - 2.75 & 0.0111 \\ \text { Z } & 0.50 & 0.16 & 3.13 & 0.0046 \\\hline\end{array}$$

-Which of the parameter estimates are statistically significant at the 1% significance level?

A) All the parameter estimates are statistically significant.
B) All parameter estimates except $\hat { b }$ are statistically significant.
C) $\hat { a }$ is not statistically significant, but all the rest of the parameter estimates are significant.
D) $\hat { c }$ is not statistically significant, but all the rest of the parameter estimates are significant.

Question 49

Refer to the following nonlinear model which relates W to P, Q, and R:
$W = a P ^ { b } Q ^ { c } R ^ { d }$
The computer output form the regression analysis is:
$$\begin{array} { r l l l l l } \text { DEPENDENTVARIAELE: } & \text { LNW } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 19 } & \mathbf { 0 . 9 0 2 3 } & 43.12 & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & \mathbf { 2 . 5 0 } & \mathbf { 0 . 4 5 } & \mathbf { 5 . 5 6 } & \mathbf { 0 . 0 0 0 1 } \\\text { LNP } & - 5.10 & 1.75 & - \mathbf { 2 . 9 1 } & \mathbf { 0 . 0 1 1 3 } \\\text { LNQ } & 12.4 & \mathbf { 3 . 2 } & \mathbf { 3 . 8 3 } & \mathbf { 0 . 0 0 1 7 } \\\text { LNR } & \mathbf { - 6 . 0 0 } & 1.5 & - 400 & \mathbf { 0 . 0 0 1 0 }\end{array}$$

-The value of R² tells us that

A) 0.9023% of the total variation in ln W is explained by the regression equation.
B) 90.23% of the total variation in ln W is explained by the regression equation.
C) 0.9023% of the total variation in P, W, and R is explained by the regression equation.
D) 0.9023% of the total variation in ln P, ln Q, and ln R is explained by the regression equation.

Question 50

A manager wishes to estimate an average cost equation of the following form:

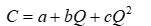
where Q is the level of output. Letting Z = Q² and using least-squares estimation, the manager obtains the following computer output:

$$\begin{array} { | c l l l l l | } \hline \text { DEPENDENT VARIABLE: } & \text { C } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ON F } \\\text { OBSERVATIONS: } & 28 & 0.7679 & 26.47 & 0.0001 & \\ \text { VARIABLE } & \begin{array} { l } \text { PARAMETER } \\\text { ESTIMATE }\end{array} & \begin{array} { l } \text { STANDARD } \\\text { ERROR }\end{array}& \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT }& 200 & 38.00 & 5.26 & 0.0001 \\\text { Q } & - 12.00 & 4.36 & - 2.75 & 0.0111 \\ \text { Z } & 0.50 & 0.16 & 3.13 & 0.0046 \\\hline\end{array}$$

-When output is 20 units, what is average cost?

A) $160
B) $200
C) $280
D) $340
E) $360

Question 51

Refer to the following nonlinear model which relates W to P, Q, and R:
$W = a P ^ { b } Q ^ { c } R ^ { d }$
The computer output form the regression analysis is:
$$\begin{array} { r l l l l l } \text { DEPENDENTVARIAELE: } & \text { LNW } & \text { R-SQUARE } & \text { F-RATIO } & \text { P-VALUE ONF } \\\text { OESERVATIONS: } & \text { 19 } & \mathbf { 0 . 9 0 2 3 } & 43.12 & \mathbf { 0 . 0 0 0 1 } & \\\\& \text { PARAMETER } & \text { STANDARD } & & \\\text { VARIAELE } & \text { ESTMMATE } & \text { ERROR } & \text { T-RATIO } & \text { P-VALUE } \\\text { INTERCEPT } & \mathbf { 2 . 5 0 } & \mathbf { 0 . 4 5 } & \mathbf { 5 . 5 6 } & \mathbf { 0 . 0 0 0 1 } \\\text { LNP } & - 5.10 & 1.75 & - \mathbf { 2 . 9 1 } & \mathbf { 0 . 0 1 1 3 } \\\text { LNQ } & 12.4 & \mathbf { 3 . 2 } & \mathbf { 3 . 8 3 } & \mathbf { 0 . 0 0 1 7 } \\\text { LNR } & \mathbf { - 6 . 0 0 } & 1.5 & - 400 & \mathbf { 0 . 0 0 1 0 }\end{array}$$

-If Q increases by 8% (all other things constant), W will

A) decrease by 99.2%.
B) decrease by 12.5%.
C) increase by 0.99%.
D) increase by 99.2%.