Deck 5: Normal, Binomial, Poisson, and Exponential Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/125
Play
Full screen (f)
Deck 5: Normal, Binomial, Poisson, and Exponential Distributions
1
The standard deviation 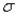 of a probability distribution is a measure of:
of a probability distribution is a measure of:
A) variability of the distribution
B) central location
C) relative likelihood
D) skewness of the distribution
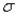 of a probability distribution is a measure of:
of a probability distribution is a measure of:A) variability of the distribution
B) central location
C) relative likelihood
D) skewness of the distribution
variability of the distribution
2
If the value of the standard normal random variable Z is positive, then the original score is where in relationship to the mean?
A) equal to the mean
B) to the left of the mean
C) to the right of the mean
D) none of these choices
A) equal to the mean
B) to the left of the mean
C) to the right of the mean
D) none of these choices
to the right of the mean
3
The normal distribution is a:
A) discrete distribution with two parameters
B) binomial distribution with only one parameter
C) density function of a discrete random variable
D) continuous distribution with two parameters
A) discrete distribution with two parameters
B) binomial distribution with only one parameter
C) density function of a discrete random variable
D) continuous distribution with two parameters
continuous distribution with two parameters
4
Given that Z is a standard normal random variable, P(-1.0 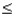 Z
Z 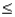 1.5) is:
1.5) is:
A) 0.7745
B) 0.8413
C) 0.0919
D) 0.9332
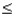 Z
Z 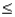 1.5) is:
1.5) is:A) 0.7745
B) 0.8413
C) 0.0919
D) 0.9332

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
5
A random variable X is standardized when each value of X has the mean of X subtracted from it, and the difference is divided by the standard deviation of X.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
6
One reason for standardizing random variables is to measure variables with:
A) different means and standard deviations on a non-standard scale
B) different means and standard deviations on a single scale
C) dissimilar means and standard deviations in like terms
D) similar means and standard deviations on two scales
A) different means and standard deviations on a non-standard scale
B) different means and standard deviations on a single scale
C) dissimilar means and standard deviations in like terms
D) similar means and standard deviations on two scales

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
7
The standard normal distribution has a mean and a standard deviation respectively equal to:
A) 0 and 0
B) 1 and 1
C) 1 and 0
D) 0 and 1
A) 0 and 0
B) 1 and 1
C) 1 and 0
D) 0 and 1

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
8
Using the standard normal distribution, the Z-score representing the 5th percentile is 1.645.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
9
The mean 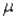 of a probability distribution is a measure of:
of a probability distribution is a measure of:
A) variability of the distribution
B) central location
C) relative likelihood
D) skewness of the distribution
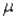 of a probability distribution is a measure of:
of a probability distribution is a measure of:A) variability of the distribution
B) central location
C) relative likelihood
D) skewness of the distribution

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
10
If the random variable X is normally distributed with mean 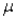 and standard deviation
and standard deviation 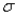 , then the random variable Z defined by
, then the random variable Z defined by 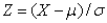 is also normally distributed with mean 0 and standard deviation 1.
is also normally distributed with mean 0 and standard deviation 1.
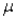 and standard deviation
and standard deviation 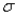 , then the random variable Z defined by
, then the random variable Z defined by 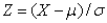 is also normally distributed with mean 0 and standard deviation 1.
is also normally distributed with mean 0 and standard deviation 1.
Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
11
The total area under the normal distribution curve is equal to one.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
12
Which equation shows the process of standardizing?
A)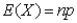
B)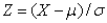
C)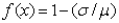
D)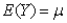
A)
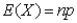
B)
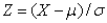
C)
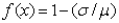
D)
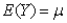

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following might not be appropriately modeled with a normal distribution?
A) the daily low temperature in Anchorage, Alaska
B) the returns on a stock
C) the daily change in inventory at a computer manufacturer
D) the salaries of employees at a large company
A) the daily low temperature in Anchorage, Alaska
B) the returns on a stock
C) the daily change in inventory at a computer manufacturer
D) the salaries of employees at a large company

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
14
Given that the random variable X is normally distributed with a mean of 80 and a standard deviation of 10, P(85 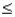 X
X 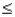 90) is:
90) is:
A) 0.5328
B) 0.3413
C) 0.1915
D) 0.1498
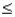 X
X 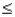 90) is:
90) is:A) 0.5328
B) 0.3413
C) 0.1915
D) 0.1498

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
15
If X is a normal random variable with a standard deviation of 10, then 3X has a standard deviation equal to:
A) 10
B) 13
C) 30
D) 90
A) 10
B) 13
C) 30
D) 90

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
16
Given that Z is a standard normal variable, the value z for which P(Z 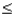 z) = 0.2580 is:
z) = 0.2580 is:
A) 0.70
B) 0.758
C) -0.65
D) 0.242
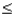 z) = 0.2580 is:
z) = 0.2580 is:A) 0.70
B) 0.758
C) -0.65
D) 0.242

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
17
If we plot a continuous probability distribution f(x), the total probability under the curve is:
A) -1
B) 0
C) 1
D) 100
A) -1
B) 0
C) 1
D) 100

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
18
What two dollar amounts, equidistant from the mean of $30, such that 98% of all customer purchases are between these values?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
19
The higher the value of the density function f(x), _____.
A) the less likely the value x
B) the more likely the value x
C) the less likely the distribution is normal
D) none of these choices is likely
A) the less likely the value x
B) the more likely the value x
C) the less likely the distribution is normal
D) none of these choices is likely

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
20
A continuous probability distribution is characterized by:
A) a list of possible values
B) counts
C) an array of individual values
D) a continuum of possible values
A) a list of possible values
B) counts
C) an array of individual values
D) a continuum of possible values

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
21
There is a 1% chance that this company will sell more than what number of cars during the next year?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
22
What number of cars, equidistant from the mean, such that 98% of car sales are between these values?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
23
The mean and standard deviation of a normally distributed random variable that has been "standardized" are zero and one, respectively.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
24
Calculate the mean, variance, and standard deviation for the entire year (assume 52 weeks in the year).

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
25
If the restaurant stocks 600 hamburgers and 150 chicken sandwiches for a given day, what is the probability that it will run out of hamburgers or chicken sandwiches (or both) that day? Assume that the demands for hamburgers and chicken sandwiches are probabilistically independent.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
26
What two dollar amounts, equidistant from the mean of $30, such that 90% of all customer purchases are between these values?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
27
What is the probability that this company will sell between 2.0 and 2.15 million cars next year?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
28
Using the standard normal distribution, the Z- score representing the 99th percentile is 2.326.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
29
How many chicken sandwiches must the restaurant stock to be 99% sure of not running out on a given day?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
30
What number of cars, equidistant from the mean, such that 90% of car sales are between these values?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
31
Using the standard normal curve, the Z- score representing the 75th percentile is 0.674.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
32
What is the probability that a randomly selected customer will spend less than $15?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
33
What is the probability that a randomly selected customer will spend $20 or more?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
34
What is the probability that a randomly selected customer will spend $30 or more?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
35
There is a 5% chance that GM will sell more than what number of cars during the next year?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
36
Using the standard normal curve, the Z- score representing the 10th percentile is 1.28.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
37
What is the probability that a randomly selected customer will spend between $20 and $35?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
38
What is the probability that this company will sell more than 2 million cars next year?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
39
A random variable X is normally distributed with a mean of 175 and a standard deviation of 50. Given that X = 150, its corresponding Z- score is -0.50.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
40
What is the probability that GM will sell between 2.0 and 2.3 million cars during the next year?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
41
A restaurant stocks 600 hamburgers and 150 chicken sandwiches for a given day. Assume that the demands for hamburgers and chicken sandwiches are probabilistically independent. Why is the independence assumption in this scenario probably not realistic? Using a more realistic assumption, do you think the probability would increase or decrease?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
42
What is the probability of getting a score higher than 85 on this exam?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
43
Only 5% of the students taking the test scored higher than what value?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
44
What percentage of students scored between 81 and 89 on this exam?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
45
According to the empirical rule, how many observations lie within +/- 2 standard deviation from the mean?
A) 50%
B) 68%
C) 95%
D) almost all
A) 50%
B) 68%
C) 95%
D) almost all

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
46
The variance of a binomial distribution is given by the formula 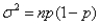 , where n is the number of trials, and p is the probability of success in any trial.
, where n is the number of trials, and p is the probability of success in any trial.
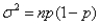 , where n is the number of trials, and p is the probability of success in any trial.
, where n is the number of trials, and p is the probability of success in any trial.
Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
47
The results of tossing a coin can be portrayed in a(n):
A) binomial distribution
B) normal distribution
C) exponential distribution
D) Poisson distribution
A) binomial distribution
B) normal distribution
C) exponential distribution
D) Poisson distribution

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
48
A binomial distribution with n number of trials, and probability of success p can be approximated well by a normal distribution with mean np and variance 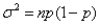 if np > 5 and n(1-p) > 5.
if np > 5 and n(1-p) > 5.
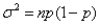 if np > 5 and n(1-p) > 5.
if np > 5 and n(1-p) > 5.
Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
49
For a given probability of success p that is not too close to 0 or 1, the binomial distribution tends to take on more of a symmetric bell shape as the number of trials n increases.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
50
The binomial distribution is a discrete distribution that deals with a sequence of identical trials, each of which has only two possible outcomes.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
51
The binomial distribution is a continuous distribution that is not far behind the normal distribution in order of importance.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
52
According to the empirical rule, how many observations lie within +/- 3 standard deviation from the mean?
A) 50%
B) 68%
C) 95%
D) almost all
A) 50%
B) 68%
C) 95%
D) almost all

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
53
The variance of a binomial distribution for which n = 100 and p = 0.20 is:
A) 100
B) 80
C) 20
D) 16
A) 100
B) 80
C) 20
D) 16

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
54
The binomial probability distribution is used with:
A) a discrete random variable
B) a continuous random variable
C) either a discrete or a continuous random variable, depending on the variance
D) either a discrete or a continuous random variable, depending on the sample size
A) a discrete random variable
B) a continuous random variable
C) either a discrete or a continuous random variable, depending on the variance
D) either a discrete or a continuous random variable, depending on the sample size

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
55
The binomial random variable represents the number of successes that occur in a specific period of time.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
56
According to the empirical rule, how many observations lie within +/- 1 standard deviation from the mean?
A) 50%
B) 68%
C) 95%
D) almost all
A) 50%
B) 68%
C) 95%
D) almost all

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
57
The density function specifies the probability distribution of a continuous random variable.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
58
Sampling done without replacement means that:
A) only certain members of the population can be sampled
B) each member of the population can be sampled repeatedly
C) each member of the population can be sampled only once
D) each member of the population can be sampled twice
A) only certain members of the population can be sampled
B) each member of the population can be sampled repeatedly
C) each member of the population can be sampled only once
D) each member of the population can be sampled twice

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
59
We assume that the outcomes of successive trials in a binomial experiment are:
A) probabilistically independent
B) probabilistically dependent
C) identical from trial to trial
D) random number between 0 and 1
A) probabilistically independent
B) probabilistically dependent
C) identical from trial to trial
D) random number between 0 and 1

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
60
How many hamburgers must the restaurant stock to be 99% sure of not running out on a given day?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
61
Find the probability distribution of X.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
62
Let Y be the number of the 12 male adults who are less than 62 inches tall. Determine the mean and standard deviation of Y.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
63
What is the probability that exactly two of the 20 new microwaves sold will require a warranty repair in the first 90 days?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
64
What is the probability that only one of the 20 new microwaves sold will require a warranty repair in the first 90 days?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
65
Find P(X < 3).

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
66
What is the probability that at most two of the 20 new microwaves sold will require a warranty repair in the first 90 days?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
67
What is the probability that exactly half the male adults will be less than 62 inches tall?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
68
What is the probability that between two and four (inclusive) of the 20 new microwaves sold will require a warranty repair in the first 90 days?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
69
What is the probability that less than two of the 20 new microwaves sold will require a warranty repair in the first 90 days?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
70
Find P(2 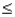 X
X 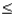 4).
4).
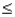 X
X 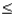 4).
4).
Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
71
What is the probability that none of the 20 new microwaves sold will require a warranty repair in the first 90 days?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
72
What is the probability that more than one of the 20 new microwaves sold will require a warranty repair in the first 90 days?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
73
The binomial distribution deals with consecutive trials, each of which has two possible outcomes.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
74
What is the probability that at least one of the 20 new microwaves sold will require a warranty repair in the first 90 days?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
75
What is the expected number of the new microwaves sold that will require a warranty repair in the first 90 days?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
76
The variance of a binomial distribution for which n = 50 and p = 0.20 is 8.0.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
77
Find the mean and the variance of X.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
78
What is the standard deviation of the number of the new microwaves sold that will require a warranty repair in the first 90 days?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
79
What type of probability distribution will most likely be used to analyze warranty repair needs on new microwaves in this situation?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
80
What is the probability that between three and six (exclusive) of the 20 new microwaves sold will require a warranty repair in the first 90 days?

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck


