Deck 16: Simulation Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/102
Play
Full screen (f)
Deck 16: Simulation Models
1
Customer loyalty models are an example of which category of simulation application?
A) operations models
B) financial models
C) marketing models
D) games of chance
E) none of these choices
A) operations models
B) financial models
C) marketing models
D) games of chance
E) none of these choices
marketing models
2
Which of the following is typically not an application of simulation models?
A) operations models
B) financial models
C) marketing models
D) value of Information models
E) none of these choices
A) operations models
B) financial models
C) marketing models
D) value of Information models
E) none of these choices
value of Information models
3
Which two random variables are typically simulated as inputs in bidding models?
A) number of bidding competitors and bid amount
B) number of bidding competitors and bid profit
C) individual bid amounts and net bidding profits
D) mean number of bidding competitors and net bidding profit
E) none of these choices
A) number of bidding competitors and bid amount
B) number of bidding competitors and bid profit
C) individual bid amounts and net bidding profits
D) mean number of bidding competitors and net bidding profit
E) none of these choices
number of bidding competitors and bid amount
4
Suppose we have a 0-1 output for whether a bidder wins a contract in a bidding model (0=bidder does not win contract, and 1=bidder wins contract). From the mean of this output, what can we determine?
A) the mean number of bidders
B) the average winning bid
C) the probability that the bidder will win the contract
D) the standard deviation of the next highest competitor's bid
E) none of these choices
A) the mean number of bidders
B) the average winning bid
C) the probability that the bidder will win the contract
D) the standard deviation of the next highest competitor's bid
E) none of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
5
You would like to develop a simulation model for estimating the time until failure of a product. Which distribution is most appropriate for your model?
A) binomial
B) gamma
C) normal
D) chi-square
A) binomial
B) gamma
C) normal
D) chi-square

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following functions is not appropriate in cases where a single simulation is run?
A) RISKMIN
B) RISKMAX
C) RISKPERCENTILE
D) RISKSIMTABLE
E) none of these choices
A) RISKMIN
B) RISKMAX
C) RISKPERCENTILE
D) RISKSIMTABLE
E) none of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
7
What is an example of a financial application in which simulation cannot be applied?
A) future stock prices
B) customer preferences for different attributes of products
C) future interest rates
D) future cash flows
A) future stock prices
B) customer preferences for different attributes of products
C) future interest rates
D) future cash flows

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
8
The value at risk (VAR) is typically defined as the:
A) 5th percentile of NPV distribution
B) 10th percentile of NPV distribution
C) 50th percentile of NPV distribution
D) 90th percentile of NPV distribution
E) 95th percentile of NPV distribution
A) 5th percentile of NPV distribution
B) 10th percentile of NPV distribution
C) 50th percentile of NPV distribution
D) 90th percentile of NPV distribution
E) 95th percentile of NPV distribution

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
9
Which function is not an @RISK statistical function?
A) RISKMIN
B) RISKMAX
C) RISKPERCENTILE
D) RISKSIMTABLE
A) RISKMIN
B) RISKMAX
C) RISKPERCENTILE
D) RISKSIMTABLE

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
10
Suppose we compare the difference between the NPV of a financial model in which the means are entered for all input random variables and the NPV of a financial model in which the most likely values are entered for all input random variables. A large difference between the NPV's demonstrate:
A) the value at risk (VAR)
B) the effect of randomness
C) the flaw of averages
D) the bias of the analyst
E) none of these choices
A) the value at risk (VAR)
B) the effect of randomness
C) the flaw of averages
D) the bias of the analyst
E) none of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
11
In a manufacturing model, we might simulate the number of days to produce a batch and the yield from each batch. The number of days would typically be a ____ distribution and the yield would be a ____ distribution.
A) continuous; discrete
B) continuous; continuous
C) discrete; continuous
D) discrete; discrete
A) continuous; discrete
B) continuous; continuous
C) discrete; continuous
D) discrete; discrete

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following is a popular distribution, especially when a right-skewed distribution of a nonnegative quantity is desired?
A) t-distribution
B) chi-square distribution
C) gamma distribution
D) normal distribution
E) all of these choices
A) t-distribution
B) chi-square distribution
C) gamma distribution
D) normal distribution
E) all of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
13
In cash flow models, we are typically interested in investigating:
A) the value at risk (VAR)
B) the net present value (NPV)
C) the amount of loans required to maintain a minimum cash balance
D) the interest on loans taken out by a firm
E) none of these choices
A) the value at risk (VAR)
B) the net present value (NPV)
C) the amount of loans required to maintain a minimum cash balance
D) the interest on loans taken out by a firm
E) none of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
14
Financial analysts may attempt to determine which of the following with simulation models?
A) mean and variance of a project NPV
B) probability that a project with have a negative NPV
C) probability that a company will have to borrow a certain amount during the next year
D) mean and variance of a company's profit during the next fiscal year
E) all of these choices
A) mean and variance of a project NPV
B) probability that a project with have a negative NPV
C) probability that a company will have to borrow a certain amount during the next year
D) mean and variance of a company's profit during the next fiscal year
E) all of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
15
Bidding for contracts is an example of which category of simulation model application?
A) operations models
B) financial models
C) marketing models
D) games of chance
E) none of these choices
A) operations models
B) financial models
C) marketing models
D) games of chance
E) none of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
16
The amount of variability of a financial output caused by different inputs can be investigated using:
A) the NPV function
B) a histogram of the NPV
C) a tornado graph of NPV
D) the value at risk (VAR)
E) all of these choices
A) the NPV function
B) a histogram of the NPV
C) a tornado graph of NPV
D) the value at risk (VAR)
E) all of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
17
Which @RISK function can be used to find the probability of a particular value in an output distribution?
A) RISKMIN
B) RISKMAX
C) RISKPERCENTILE
D) RISKTARGET
E) none of these choices
A) RISKMIN
B) RISKMAX
C) RISKPERCENTILE
D) RISKTARGET
E) none of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
18
Financial analysts often investigate the value at risk (VAR) with simulation models. VAR is an indicator of:
A) how much to bid for a project
B) the expected amount of loss for a project
C) what is nearly the worst possible outcome for a project
D) the required amount of investment required for a project
E) none of these choices
A) how much to bid for a project
B) the expected amount of loss for a project
C) what is nearly the worst possible outcome for a project
D) the required amount of investment required for a project
E) none of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
19
Cash balance models are an example of which category of simulation application?
A) operations models
B) financial models
C) marketing models
D) games of chance
E) none of these choices
A) operations models
B) financial models
C) marketing models
D) games of chance
E) none of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
20
Which function is often required in simulations where we must model a process over multiple time periods and take the uncertain timing of events into account?
A) RISKMIN
B) RISKMAX
C) NPV
D) IF
E) none of these choices
A) RISKMIN
B) RISKMAX
C) NPV
D) IF
E) none of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
21
Uncertain timing and the events that follow in process modeling can be modeled using IF statements.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
22
We can use the RISKSIMTABLE function to summarize the results of a single simulation of product lifetime.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
23
In Excel®, we can use the RAND function inside an IF function to simulate whether some event occurs or does not occur.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
24
Using @RISK summary functions such as RISKMEAN, RISKPERCENTILE, and others allows us to capture simulation results in the same worksheet as the simulation model.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
25
In warranty cost models, the key input random variable is product lifetime.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
26
Although we can determine the optimal bid and the expected profit from that bid in a bidding simulation, we usually cannot determine the probability of winning.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
27
The primary objective in simulation models of bidding for contracts is to determine the optimal bid.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
28
The random nature of games of chance make them poor candidates for simulation.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
29
A common distribution for modeling product lifetimes is the binomial distribution.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
30
In investment models, a useful approach for generating future returns and inflation factors from historical data is:
A) the NPV approach
B) the scenario approach
C) the averaging approach
D) the trend analysis approach
E) none of these choices
A) the NPV approach
B) the scenario approach
C) the averaging approach
D) the trend analysis approach
E) none of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
31
Churn is an example of the type of uncertain variable we deal with in financial models.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
32
The main topic of investigation in marketing and sales models is the:
A) amount invested in marketing
B) timing of marketing
C) profit from sales
D) timing of sales
E) tradeoff between marketing and sales
A) amount invested in marketing
B) timing of marketing
C) profit from sales
D) timing of sales
E) tradeoff between marketing and sales

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
33
RISKTARGET is a function that allows us to determine the cumulative probability of a particular value in an output distribution, such as the probability of meeting a due date in manufacturing.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
34
A key input variable in many marketing models of customer loyalty is the:
A) mean profit per customer
B) number of customers
C) churn rate
D) time horizon
E) all of these choices
A) mean profit per customer
B) number of customers
C) churn rate
D) time horizon
E) all of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
35
In a manufacturing setting, a discrete distribution is natural for modeling the number of days to produce a batch, and a continuous distribution is appropriate for modeling the yield from a batch.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
36
In a bidding model, once we have a bidding strategy that maximizes the expected profit, we should no longer consider the bidder's aversion to risk.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
37
In a marketing and sales model, what might be a good choice for a discrete distribution to model the random timing of sales?
A) logarithmic distribution
B) normal distribution
C) binomial distribution
D) exponential distribution
E) Poisson distribution
A) logarithmic distribution
B) normal distribution
C) binomial distribution
D) exponential distribution
E) Poisson distribution

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
38
In bidding models, the simulation input variable is the number of competitors who will bid.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
39
Which tasks are considered to be marketing applications of simulation modeling?
A) determining the effect of entry of new brands into the market
B) discovering customer preferences for different attributes of products
C) investigating brand-switching behavior of customers
D) investigating the effect of advertising on sales
E) all of these choices
A) determining the effect of entry of new brands into the market
B) discovering customer preferences for different attributes of products
C) investigating brand-switching behavior of customers
D) investigating the effect of advertising on sales
E) all of these choices

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
40
RISKMAX and RISKMIN are can be used to find the probability of meeting a given due date in a manufacturing model.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
41
Using the information from the pro forma and the distribution of the NPV, determine the chances the firm could loose money on this project, given the price uncertainty.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
42
Given the information in the pro forma, the NPV, and the risk of a loss, would you invest in this project?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
43
A firm is considering investing $0.9M in a typical industrial manufacturing application with a three-year production planning cycle under a forecasted market price environment. A simple three-period project pro forma cash flow sheet for this project is shown below: 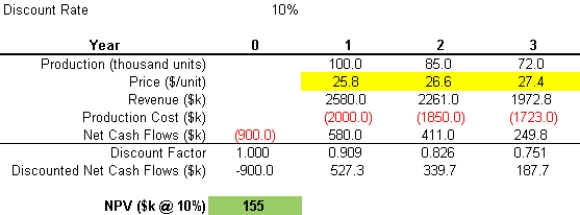 In the pro forma, the production and price forecast in each period translate to revenue, which can then be netted of production costs to arrive at the expected cash flow in each period. The cash flows are then discounted at a rate that is commensurate with the riskiness of the project (here, assumed to be 10%).
In the pro forma, the production and price forecast in each period translate to revenue, which can then be netted of production costs to arrive at the expected cash flow in each period. The cash flows are then discounted at a rate that is commensurate with the riskiness of the project (here, assumed to be 10%).
The Net Present Value (NPV) is the sum of the discounted cash flows. What is the NPV of the project, including the required investment?
 In the pro forma, the production and price forecast in each period translate to revenue, which can then be netted of production costs to arrive at the expected cash flow in each period. The cash flows are then discounted at a rate that is commensurate with the riskiness of the project (here, assumed to be 10%).
In the pro forma, the production and price forecast in each period translate to revenue, which can then be netted of production costs to arrive at the expected cash flow in each period. The cash flows are then discounted at a rate that is commensurate with the riskiness of the project (here, assumed to be 10%).The Net Present Value (NPV) is the sum of the discounted cash flows. What is the NPV of the project, including the required investment?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
44
In marketing models of customer loyalty, we are typically interested in modeling the rate of customer retention, called churn.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose that the forecasted price levels shown in the pro forma cash flow sheet are not deterministic, but rather, are expected to fluctuate due to market forces. The prices are expected to be normally distributed in each year, with the means equal to the expected values shown in the pro forma, but with standard deviations of $5.2, $5.3, and $5.5 in years 1, 2, and 3, respectively. Enter this pro forma in an Excel worksheet, with the appropriate @RISK functions for the random prices, and simulate 1,000 iterations. What is the expected NPV now? Would you recommend investing in this project? Explain.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
46
In financial simulation models, the value at risk (VAR) is the 5th percentile of an output distribution, and it indicates nearly the worst possible outcome.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
47
Using the information from the pro forma, determine the standard deviation of the NPV. What does it indicate?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
48
In investment models, we typically must simulate the random investment weights.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
49
A key objective in cash flow models is often to determine the amount of debt that must be taken out to maintain a minimum cash balance.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
50
A tornado graph lets us see which random input has the greatest effect on a specified output in a financial model.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
51
Simulate Amanda's portfolio over the next 30 years and determine how much she can expect to have in her account at the end of that period. At the beginning of each year, compute the beginning balance in Amanda's account. Note that this balance is either 0 (for year 1) or equal to the ending balance of the previous year. The contribution of $5,000 is then added to calculate the new balance. The market return for each year is given by a normal random variable with the parameters above (assume the market returns in each year are independent of the other years). The ending balance for each year is then equal to the beginning balance, augmented by the contribution, and multiplied by (1+Market return). Suppose Amanda will stop investing in the stock market and transfer all of her retirement into a savings account if and when she reaches $500,000. When can she expect to reach this goal?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
52
Simulate Amanda's portfolio over the next 30 years and determine how much she can expect to have in her account at the end of that period. At the beginning of each year, compute the beginning balance in Amanda's account. Note that this balance is either 0 (for year 1) or equal to the ending balance of the previous year. The contribution of $5,000 is then added to calculate the new balance. The market return for each year is given by a normal random variable with the parameters above (assume the market returns in each year are independent of the other years). The ending balance for each year is then equal to the beginning balance, augmented by the contribution, and multiplied by (1+Market return).

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
53
Simulate Amanda's portfolio over the next 30 years and determine how much she can expect to have in her account at the end of that period. At the beginning of each year, compute the beginning balance in Amanda's account. Note that this balance is either 0 (for year 1) or equal to the ending balance of the previous year. The contribution of $5,000 is then added to calculate the new balance. The market return for each year is given by a normal random variable with the parameters above (assume the market returns in each year are independent of the other years). The ending balance for each year is then equal to the beginning balance, augmented by the contribution, and multiplied by (1+Market return). What is the standard deviation of the ending balance? What does the distribution look like? What should Amanda infer from this?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
54
The @RISK function RISKUNIFORM (0,1) is essentially equivalent to RAND().

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
55
In financial simulation models, we are typically more interested in the expected NPV of a project than in the extremes of the outcomes.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
56
A @RISK output range allows us to obtain a summary chart that shows the entire simulated range at once.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
57
Simulate Amanda's portfolio over the next 30 years and determine how much she can expect to have in her account at the end of that period. At the beginning of each year, compute the beginning balance in Amanda's account. Note that this balance is either 0 (for year 1) or equal to the ending balance of the previous year. The contribution of $5,000 is then added to calculate the new balance. The market return for each year is given by a normal random variable with the parameters above (assume the market returns in each year are independent of the other years). The ending balance for each year is then equal to the beginning balance, augmented by the contribution, and multiplied by (1+Market return). What is the probability that Amanda will have less than $500,000 in her retirement account after 30 years?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
58
In marketing and sales models, the primary source of uncertainty is the timing of sales.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
59
Suppose we are using a marketing simulation model to determine the expected profit under conditions of uncertain customer loyalty. In this case, we should use an optimization model to determine the optimal amount to spend on increasing customer loyalty.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
60
Using the information from the pro forma, discuss what the distribution of the NPV looks like.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
61
Consider a customer whose first car is GM. If profits are discounted at 10% annually, use simulation to estimate the value of this customer to GM over the customer's lifetime.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
62
Suppose first that all three bidders are aware of the winner's curse so they have decided (independently) to bid 10% below their estimated values. Using 1000 iterations report the expected profit (or loss) to the winner.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
63
Suppose that Coke® and Pepsi® are in a fierce competition for the cola market. Each week each person in the market buys one case of Coke® or Pepsi®. If the person's last purchase was Coke®, there is a 0.80 probability that this person's next purchase will be Coke®; otherwise, it will be Pepsi®. (We are considering only two brands in the market in this scenario.) Similarly, if the person's last purchase was Pepsi®, there is a 0.90 probability that this person's next purchase will be Pepsi®; otherwise, it will be Coke®. Currently half of all people purchase Coke®, and the other half purchase Pepsi®. Simulate one year of sales in the cola market and estimate each company's average weekly market share. Do this by assuming that the total market size is fixed at 100 customers. (Hint: Use the RISKBINOMIAL function.)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
64
What if the GM satisfaction rate is raised further to 90%. What would the customer NPV be in that case?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
65
Simulate Amanda's portfolio over the next 30 years and determine how much she can expect to have in her account at the end of that period. At the beginning of each year, compute the beginning balance in Amanda's account. Note that this balance is either 0 (for year 1) or equal to the ending balance of the previous year. The contribution of $5,000 is then added to calculate the new balance. The market return for each year is given by a normal random variable with the parameters above (assume the market returns in each year are independent of the other years). The ending balance for each year is then equal to the beginning balance, augmented by the contribution, and multiplied by (1+Market return).
Next, suppose Amanda's broker thinks the stock market may be too risky and has advised her to diversity by investing some of her money in money market funds and bonds. He estimates that this will lower her expected annual return to 10% per year, but will also lower the standard deviation to 10%. What is the standard deviation of the ending balance? What does the distribution look like now? What should Amanda infer from this?
Next, suppose Amanda's broker thinks the stock market may be too risky and has advised her to diversity by investing some of her money in money market funds and bonds. He estimates that this will lower her expected annual return to 10% per year, but will also lower the standard deviation to 10%. What is the standard deviation of the ending balance? What does the distribution look like now? What should Amanda infer from this?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
66
Perform a simulation assuming the plant will be designed to meet the expected demand. Use RISKSIMTABLE with a range of possible values to help the firm decide what the plant capacity should be. Which simulation yields the largest median NPV?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
67
Perform a simulation assuming the plant will be designed to meet the expected demand. Use RISKSIMTABLE with a range of possible values to help the firm decide what the plant capacity should be. Which simulation has the most risk as measured by spread or dispersion in the data? Please state clearly what statistic you used to answer this question.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
68
Simulate Amanda's portfolio over the next 30 years and determine how much she can expect to have in her account at the end of that period. At the beginning of each year, compute the beginning balance in Amanda's account. Note that this balance is either 0 (for year 1) or equal to the ending balance of the previous year. The contribution of $5,000 is then added to calculate the new balance. The market return for each year is given by a normal random variable with the parameters above (assume the market returns in each year are independent of the other years). The ending balance for each year is then equal to the beginning balance, augmented by the contribution, and multiplied by (1+Market return).
Next, suppose Amanda's broker thinks the stock market may be too risky and has advised her to diversity by investing some of her money in money market funds and bonds. He estimates that this will lower her expected annual return to 10% per year, but will also lower the standard deviation to 10%. What can she expect to have in her account after thirty years under this investing strategy?
Next, suppose Amanda's broker thinks the stock market may be too risky and has advised her to diversity by investing some of her money in money market funds and bonds. He estimates that this will lower her expected annual return to 10% per year, but will also lower the standard deviation to 10%. What can she expect to have in her account after thirty years under this investing strategy?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
69
Perform a simulation assuming the plant will be designed to meet the expected demand. Use RISKSIMTABLE with a range of possible values to help the firm decide what the plant capacity should be. Are there any simulations which indicated there was a chance of getting negative NPV? Briefly explain in one sentence.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
70
Perform a simulation assuming the plant will be designed to meet the expected demand. Use RISKSIMTABLE with a range of possible values to help the firm decide what the plant capacity should be.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
71
Perform a simulation assuming the plant will be designed to meet the expected demand. What is the NPV in that case?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
72
Assume that one of the bidders bids 20% below his or her estimated value, while the other two bidders bid 10% below their estimated values. Using 1000 iterations, report the expected profit or loss to the conservative bidder. What is the probability of winning for the conservative bidder?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
73
Suppose that a customer satisfaction firm approaches GM with a proposal to increase satisfaction from the current 80% rate to $85% through a low cost maintenance program that will cost GM $300 per customer. Would the program be worth it?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
74
Assume that one of the bidders bids 20% below his or her estimated value, while the other two bidders bid 10% below their estimated values. Using 1000 iterations, report the expected profit or loss to the conservative bidder.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
75
Suppose GM could raise it customer satisfaction to 85%, to match Toyota's. What would the customer NPV be in that case?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
76
What is the probability of winning for each bidder in the above scenario?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
77
Assume 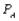 = 0.10,
= 0.10, 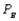 = 0.15, and
= 0.15, and 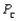 = 0.20. Suppose a 1% increase in market share is worth $10,000 per week to company A. Company A believes that for a cost of $1 million per year it can cut the percentage of unsatisfactory juice cartons in half. Is this worthwhile?
= 0.20. Suppose a 1% increase in market share is worth $10,000 per week to company A. Company A believes that for a cost of $1 million per year it can cut the percentage of unsatisfactory juice cartons in half. Is this worthwhile?
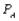 = 0.10,
= 0.10, 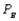 = 0.15, and
= 0.15, and 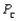 = 0.20. Suppose a 1% increase in market share is worth $10,000 per week to company A. Company A believes that for a cost of $1 million per year it can cut the percentage of unsatisfactory juice cartons in half. Is this worthwhile?
= 0.20. Suppose a 1% increase in market share is worth $10,000 per week to company A. Company A believes that for a cost of $1 million per year it can cut the percentage of unsatisfactory juice cartons in half. Is this worthwhile?
Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
78
Simulate Amanda's portfolio over the next 30 years and determine how much she can expect to have in her account at the end of that period. At the beginning of each year, compute the beginning balance in Amanda's account. Note that this balance is either 0 (for year 1) or equal to the ending balance of the previous year. The contribution of $5,000 is then added to calculate the new balance. The market return for each year is given by a normal random variable with the parameters above (assume the market returns in each year are independent of the other years). The ending balance for each year is then equal to the beginning balance, augmented by the contribution, and multiplied by (1+Market return).
Next, suppose Amanda's broker thinks the stock market may be too risky and has advised her to diversity by investing some of her money in money market funds and bonds. He estimates that this will lower her expected annual return to 10% per year, but will also lower the standard deviation to 10%. Suppose again that Amanda will stop investing in the stock market and transfer all of her retirement into a savings account if and when she reaches $500,000. When can she expect to reach this goal under the more conservative investing strategy?
Next, suppose Amanda's broker thinks the stock market may be too risky and has advised her to diversity by investing some of her money in money market funds and bonds. He estimates that this will lower her expected annual return to 10% per year, but will also lower the standard deviation to 10%. Suppose again that Amanda will stop investing in the stock market and transfer all of her retirement into a savings account if and when she reaches $500,000. When can she expect to reach this goal under the more conservative investing strategy?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
79
Suppose that a recent study shows that each week each of 300 families buys a gallon of apple juice from company A, B, or C. Let 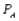 denote the probability that a gallon produced by company A is of unsatisfactory quality, and define
denote the probability that a gallon produced by company A is of unsatisfactory quality, and define 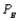 and
and 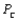 similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands.
similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands.
After a year, what will the market share for each of the three companies be? Assume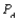 = 0.10,
= 0.10, 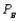 = 0.15, and
= 0.15, and 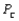 = 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.)
= 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.)
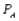 denote the probability that a gallon produced by company A is of unsatisfactory quality, and define
denote the probability that a gallon produced by company A is of unsatisfactory quality, and define 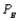 and
and 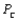 similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands.
similarly for companies B and C. If the last gallon of juice purchased by a family is satisfactory, the next week they will purchase a gallon of juice from the same company. If the last gallon of juice purchased by a family is not satisfactory, then the family will purchase a gallon from a competitor. Consider one week in which A families have purchased juice A, B families have purchased juice B, and C families have purchased juice C. Assume that families that switch brands during a period are allocated to the remaining brands in a manner that is proportional to the current market shares of the other brands. Thus, if a customer switches from brand A, there is probability B/(B + C) that he will switch to brand B and probability C/(B + C) that he will switch to brand C. Suppose that the market is currently divided equally: 100 families for each of the three brands.After a year, what will the market share for each of the three companies be? Assume
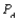 = 0.10,
= 0.10, 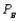 = 0.15, and
= 0.15, and 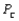 = 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.)
= 0.20. (Hint: Use the RISKBINOMIAL function to model how many people switch from A, then how many switch from A to B and from A to C.)
Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
80
Simulate Amanda's portfolio over the next 30 years and determine how much she can expect to have in her account at the end of that period. At the beginning of each year, compute the beginning balance in Amanda's account. Note that this balance is either 0 (for year 1) or equal to the ending balance of the previous year. The contribution of $5,000 is then added to calculate the new balance. The market return for each year is given by a normal random variable with the parameters above (assume the market returns in each year are independent of the other years). The ending balance for each year is then equal to the beginning balance, augmented by the contribution, and multiplied by (1+Market return).
Next, suppose Amanda's broker thinks the stock market may be too risky and has advised her to diversity by investing some of her money in money market funds and bonds. He estimates that this will lower her expected annual return to 10% per year, but will also lower the standard deviation to 10%. What is the probability that Amanda will have less than $500,000 in her retirement account after 30 years under the more conservative investing strategy?
Next, suppose Amanda's broker thinks the stock market may be too risky and has advised her to diversity by investing some of her money in money market funds and bonds. He estimates that this will lower her expected annual return to 10% per year, but will also lower the standard deviation to 10%. What is the probability that Amanda will have less than $500,000 in her retirement account after 30 years under the more conservative investing strategy?

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck


