Deck 16: Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/115
Play
Full screen (f)
Deck 16: Analysis of Variance
1
Which of the following best describes an experimental design model where the treatments are defined as the levels of one factor, and the experimental design specifies independent samples?
A) Randomised block design
B) Two way ANOVA
C) One way ANOVA
D) All of these choices are correct.
A) Randomised block design
B) Two way ANOVA
C) One way ANOVA
D) All of these choices are correct.
C
2
In an ANOVA test, the test statistic is F = 3.08. The rejection region is F > 3.07 for the 5% level of significance, F > 3.82 for the 2.5% level, and F > 4.87 for the 1% level. For this test, the p-value is:
A) greater than 0.05.
B) between 0.01 and 0.025.
C) between 0.025 and 0.05.
D) smaller than 0.01.
A) greater than 0.05.
B) between 0.01 and 0.025.
C) between 0.025 and 0.05.
D) smaller than 0.01.
C
3
One-way ANOVA is applied to three independent samples having means 10, 13 and 18, respectively. If each observation in the first sample were decreased by 5, the value of the F-statistic would:
A) increase.
B) decrease.
C) remain unchanged.
D) decrease by 5.
A) increase.
B) decrease.
C) remain unchanged.
D) decrease by 5.
B
4
Which of the following is true of the F-distribution?
A) It is skewed to the right.
B) Its values are always positive.
C) It is used in the ANOVA test.
D) All of these choices are correct
A) It is skewed to the right.
B) Its values are always positive.
C) It is used in the ANOVA test.
D) All of these choices are correct

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
5
In one-way ANOVA, suppose that there are four treatments with n1 = 7, n2 = 6, n3 = 5, and n4 = 7. Then the rejection region for this test at the 1% level of significance is:
A) F > F0.05,3,24.
B) F > F0.025,3,21.
C) F > F0.025,3,24.
D) F > F0.01,3,21.
A) F > F0.05,3,24.
B) F > F0.025,3,21.
C) F > F0.025,3,24.
D) F > F0.01,3,21.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
6
The test statistic of the single-factor ANOVA equals:
A) sum of squares for treatments/sum of squares for error.
B) sum of squares for error/sum of squares for treatments.
C) mean square for treatments/mean square for error.
D) mean square for error/mean square for treatments.
A) sum of squares for treatments/sum of squares for error.
B) sum of squares for error/sum of squares for treatments.
C) mean square for treatments/mean square for error.
D) mean square for error/mean square for treatments.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following is compared in ANOVA ?
A) Two or more population standard deviations.
B) Two or more population means.
C) Two or more population variances.
D) All of these choices are correct.
A) Two or more population standard deviations.
B) Two or more population means.
C) Two or more population variances.
D) All of these choices are correct.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
8
Two independent samples of size 30 each have been selected at random from the female and male students of a university. To test whether there is any difference in the grade point average between female and male students, an equal-variances t-test will be considered. Another test to consider is ANOVA. Which of the following is the most likely ANOVA to fit this test situation?
A) Randomised block design.
B) Two-way ANOVA.
C) One-way ANOVA.
D) Chi-squared test.
A) Randomised block design.
B) Two-way ANOVA.
C) One-way ANOVA.
D) Chi-squared test.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
9
In one-way ANOVA, the amount of total variation that is unexplained is measured by the:
A) sum of squares for treatments.
B) sum of squares for error.
C) total sum of squares.
D) number of degrees of freedom.
A) sum of squares for treatments.
B) sum of squares for error.
C) total sum of squares.
D) number of degrees of freedom.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
10
In a two-tailed pooled-variance t-test (equal-variances t-test), the null and alternative hypotheses are exactly the same as in one-way ANOVA with:
A) exactly one treatment.
B) exactly two treatments.
C) exactly three treatments.
D) any number of treatments.
A) exactly one treatment.
B) exactly two treatments.
C) exactly three treatments.
D) any number of treatments.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
11
In a one-way ANOVA where there are k treatments and n observations, the numbers of degrees of freedom for the F-statistic are equal to:
A) k - 1 and n - 1.
B) k - 1 and n - k.
C) n - k and k - 1.
D) nk - 1 and k - 1.
A) k - 1 and n - 1.
B) k - 1 and n - k.
C) n - k and k - 1.
D) nk - 1 and k - 1.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
12
The following equation applies to which ANOVA model? SS(Total) = SST + SSE.
A) One-way ANOVA.
B) Two-way ANOVA.
C) Completely randomised design.
D) Randomised block design.
A) One-way ANOVA.
B) Two-way ANOVA.
C) Completely randomised design.
D) Randomised block design.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
13
In ANOVA, error variability is computed as the sum of the squared errors, SSE, for all values of the response variable. This variability is the:
A) total variation.
B) within-group variation.
C) between-groups variation.
D) None of these choices are correct.
A) total variation.
B) within-group variation.
C) between-groups variation.
D) None of these choices are correct.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following statements is true?
A) The sum of squares for treatments (SST) explains some of the variation.
B) The sum of squares for error (SSE) measures the amount of variation that is unexplained.
C) SS(Total) = SST + SSE
D) All of these choices are correct.
A) The sum of squares for treatments (SST) explains some of the variation.
B) The sum of squares for error (SSE) measures the amount of variation that is unexplained.
C) SS(Total) = SST + SSE
D) All of these choices are correct.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
15
The F-statistic in a one-way ANOVA represents the variation:
A) between the treatments plus the variation within the treatments.
B) within the treatments minus the variation between the treatments.
C) between the treatments divided by the variation within the treatments.
D) variation within the treatments divided by the variation between the treatments.
A) between the treatments plus the variation within the treatments.
B) within the treatments minus the variation between the treatments.
C) between the treatments divided by the variation within the treatments.
D) variation within the treatments divided by the variation between the treatments.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following is the primary interest of designing a randomised block experiment?
A) Reduce the variation among blocks.
B) Reduce the within-treatments variation to more easily detect differences among the treatment means.
C) Increase the between-treatments variation to more easily detect differences among the treatment means.
D) Increase the total sum of squares.
A) Reduce the variation among blocks.
B) Reduce the within-treatments variation to more easily detect differences among the treatment means.
C) Increase the between-treatments variation to more easily detect differences among the treatment means.
D) Increase the total sum of squares.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
17
Which of the following is a required condition for one-way ANOVA?
A) The populations must all be normally distributed.
B) The population variances must be equal.
C) The samples for each treatment must be selected randomly and independently.
D) All of these choices are correct.
A) The populations must all be normally distributed.
B) The population variances must be equal.
C) The samples for each treatment must be selected randomly and independently.
D) All of these choices are correct.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following best describes the distribution of the test statistic for ANOVA?
A) Normal distribution and the F distribution.
B) Student t distribution.
C) Chi-squared distribution.
D) F distribution.
A) Normal distribution and the F distribution.
B) Student t distribution.
C) Chi-squared distribution.
D) F distribution.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
19
In a single-factor analysis of variance, MST is the mean square for treatments and MSE is the mean square for error. The null hypothesis of equal population means is likely false if:
A) MST is much larger than MSE.
B) MST is much smaller than MSE.
C) MST is equal to MSE.
D) MST is zero.
A) MST is much larger than MSE.
B) MST is much smaller than MSE.
C) MST is equal to MSE.
D) MST is zero.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
20
If we want to conduct a test to determine whether a population mean is greater than another population mean, we:
A) can use the analysis of variance.
B) must use the independent-samples t-test for the difference between two means.
C) must use the chi-squared test.
D) can use the analysis of variance or can use the independent-samples t-test for the difference between two means.
A) can use the analysis of variance.
B) must use the independent-samples t-test for the difference between two means.
C) must use the chi-squared test.
D) can use the analysis of variance or can use the independent-samples t-test for the difference between two means.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
21
When the effect of a level for one factor depends on which level of another factor is present, the most appropriate ANOVA design to use in this situation is the:
A) one-way ANOVA.
B) two-way ANOVA.
C) randomised block design.
D) matched pairs design.
A) one-way ANOVA.
B) two-way ANOVA.
C) randomised block design.
D) matched pairs design.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
22
Which of the following best describes the between-treatments in single-factor analysis of variance?
A) Sum of squares for error.
B) Total sum of squares.
C) Sum of squares for treatments.
D) All of these choices are correct.
A) Sum of squares for error.
B) Total sum of squares.
C) Sum of squares for treatments.
D) All of these choices are correct.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
23
In the one-way ANOVA where k is the number of treatments and n is the number of observations in all samples, the number of degrees of freedom for treatments is given by:
A) k - 1.
B) n - k.
C) n - 1.
D) n - k + 1.
A) k - 1.
B) n - k.
C) n - 1.
D) n - k + 1.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
24
A professor of statistics at Wayne State University in the US wants to determine whether the average starting salaries among graduates of the 15 universities in Michigan are equal. A sample of 25 recent graduates from each university is randomly taken. The appropriate critical value for the ANOVA test is obtained from the F-distribution with number so of degrees of freedom equal to:
A) 15 and 25.
B) 14 and 360.
C) 360 and 14.
D) 25 and 15.
A) 15 and 25.
B) 14 and 360.
C) 360 and 14.
D) 25 and 15.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
25
In single-factor analysis of variance, if large differences exist among the sample means, it is then reasonable to:
A) reject the null hypothesis.
B) reject the alternative hypothesis.
C) fail to reject the null hypothesis.
D) None of these choices are correct.
A) reject the null hypothesis.
B) reject the alternative hypothesis.
C) fail to reject the null hypothesis.
D) None of these choices are correct.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
26
A survey will be conducted to compare the grade point averages of US high-school students from four different school districts. Students are to be randomly selected from each of the four districts and their grade point averages recorded. The ANOVA model most likely to fit this situation is:
A) one-way ANOVA.
B) two-way ANOVA.
C) randomised block design.
D) complete 4 * 4 factorial design.
A) one-way ANOVA.
B) two-way ANOVA.
C) randomised block design.
D) complete 4 * 4 factorial design.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
27
One-way ANOVA is applied to independent samples taken from four normally distributed populations with equal variances. If the null hypothesis is rejected, then we can infer that:
A) all population means are equal.
B) all population means differ.
C) at least two population means are equal.
D) at least two population means differ.
A) all population means are equal.
B) all population means differ.
C) at least two population means are equal.
D) at least two population means differ.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
28
Which of the following is not a required condition for one-way ANOVA?
A) The populations are normally distributed.
B) The population variances are equal.
C) The samples are selected independently of each other.
D) The population means are equal.
A) The populations are normally distributed.
B) The population variances are equal.
C) The samples are selected independently of each other.
D) The population means are equal.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
29
In ANOVA, the F-test is the ratio of two sample variances. In the one-way ANOVA (completely randomised design), the variance used as the denominator of the ratio is the:
A) mean square for treatments.
B) mean square for error.
C) mean square for blocks.
D) total sum of squares.
A) mean square for treatments.
B) mean square for error.
C) mean square for blocks.
D) total sum of squares.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
30
In the one-way ANOVA where k is the number of treatments and n is the number of observations in all samples, the number of degrees of freedom for error is given by:
A) k - 1.
B) n - k.
C) n - 1.
D) n - k + 1.
A) k - 1.
B) n - k.
C) n - 1.
D) n - k + 1.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
31
In one-way analysis of variance, within-treatments variation stands for the:
A) sum of squares for error.
B) sum of squares for treatments.
C) total sum of squares.
D) None of these choices are correct.
A) sum of squares for error.
B) sum of squares for treatments.
C) total sum of squares.
D) None of these choices are correct.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
32
One-way ANOVA is performed on independent samples taken from three normally distributed populations with equal variances. The following summary statistics were calculated: 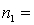 7,
7, 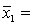 65,
65, 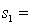 4.2.
4.2. 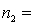 8,
8, 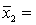 59,
59, 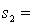 4.9.
4.9. 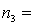 9,
9, 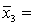 63,
63, 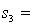 4.6. The value of the test statistics, F, equals:
4.6. The value of the test statistics, F, equals:
A) 71.250.
B) 0.322.
C) 21.104.
D) 3.376.
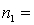 7,
7, 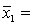 65,
65, 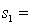 4.2.
4.2. 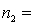 8,
8, 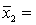 59,
59, 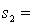 4.9.
4.9. 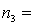 9,
9, 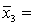 63,
63, 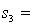 4.6. The value of the test statistics, F, equals:
4.6. The value of the test statistics, F, equals:A) 71.250.
B) 0.322.
C) 21.104.
D) 3.376.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
33
Consider the following partial ANOVA table:  The numbers of degrees of freedom for numerator and denominator, respectively, (identified by asterisks) are:
The numbers of degrees of freedom for numerator and denominator, respectively, (identified by asterisks) are:
A) 4 and 15.
B) 3 and 16.
C) 15 and 4.
D) 16 and 3.
 The numbers of degrees of freedom for numerator and denominator, respectively, (identified by asterisks) are:
The numbers of degrees of freedom for numerator and denominator, respectively, (identified by asterisks) are:A) 4 and 15.
B) 3 and 16.
C) 15 and 4.
D) 16 and 3.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
34
Which of the following is a correct formulation for the null hypothesis in one-way ANOVA?
A)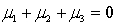 .
.
B)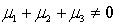 .
.
C)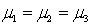 .
.
D)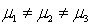 .
.
A)
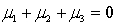 .
.B)
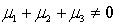 .
.C)
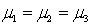 .
.D)
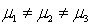 .
.
Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
35
Which of the following is not true of Tukey's multiple comparison method?
A) It is based on the studentised range statistic q to obtain the critical value needed to construct individual confidence intervals.
B) It requires that all sample sizes are equal, or at least similar.
C) It can be employed instead of the analysis of variance.
D) All of these choices are correct.
A) It is based on the studentised range statistic q to obtain the critical value needed to construct individual confidence intervals.
B) It requires that all sample sizes are equal, or at least similar.
C) It can be employed instead of the analysis of variance.
D) All of these choices are correct.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
36
The randomised block design with exactly two treatments is equivalent to a two-tailed:
A) independent samples z-test.
B) independent-samples equal-variances t-test.
C) independent-samples unequal-variances t-test.
D) matched pairs t-test.
A) independent samples z-test.
B) independent-samples equal-variances t-test.
C) independent-samples unequal-variances t-test.
D) matched pairs t-test.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
37
One-way ANOVA is performed on independent samples taken from three normally distributed populations with equal variances. The following summary statistics are calculated: 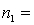 6,
6, 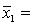 50,
50, 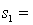 5.2.
5.2. 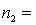 8,
8, 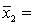 55,
55, 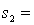 4.9 .
4.9 . 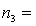 6,
6, 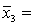 51,
51, 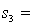 5.4. The grand mean equals:
5.4. The grand mean equals:
A) 50.0.
B) 52.0.
C) 52.3.
D) 53.0.
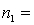 6,
6, 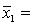 50,
50, 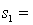 5.2.
5.2. 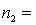 8,
8, 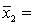 55,
55, 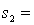 4.9 .
4.9 . 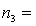 6,
6, 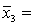 51,
51, 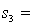 5.4. The grand mean equals:
5.4. The grand mean equals:A) 50.0.
B) 52.0.
C) 52.3.
D) 53.0.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
38
Three tennis players, one a beginner, one intermediate and one advanced, have been randomly selected from the membership of a club in a large city. Using the same tennis ball, each player hits ten serves, one with each of three racquet models, with the three racquet models selected randomly. The speed of each serve is measured with a machine and the result recorded. Among the ANOVA models listed below, the most likely model to fit this situation is the:
A) one-way ANOVA.
B) two-way ANOVA.
C) randomised block design.
D) matched-pairs model.
A) one-way ANOVA.
B) two-way ANOVA.
C) randomised block design.
D) matched-pairs model.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
39
One-way ANOVA is performed on three independent samples with n1 = 10, n2 = 8 and n3 = 9. The critical value obtained from the F-table for this test at the 5% level of significance equals:
A) 39.46.
B) 3.40.
C) 4.32.
D) 19.45.
A) 39.46.
B) 3.40.
C) 4.32.
D) 19.45.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
40
In the randomised block design ANOVA, the sum of squares for error equals:
A) SS(Total) - SST.
B) SS(Total) - SSB.
C) SS(Total) - SST - SSB.
D) SS(Total) - SS(A) - SS(B) - SS(AB).
A) SS(Total) - SST.
B) SS(Total) - SSB.
C) SS(Total) - SST - SSB.
D) SS(Total) - SS(A) - SS(B) - SS(AB).

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
41
If we examine two or more independent samples to determine if their population means could be equal, we are performing one-way analysis of variance (ANOVA).

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
42
Given the significance level 0.05, the F-value for the numbers of degrees of freedom d.f. = (9, 6) is 4.10.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
43
When the data are obtained through a controlled experiment in the single-factor ANOVA, we call the experimental design the completely randomised design of the analysis of variance.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
44
Statistics practitioners use the analysis of variance (ANOVA) technique to compare two or more populations of interval data.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
45
Three tennis players, one a beginner, one experienced and one a professional, have been randomly selected from the membership of a large city tennis club. Using the same ball, each person hits four serves with each of five racquet models, with the five racquet models selected randomly. Each serve is clocked with a radar gun and the result recorded. Among ANOVA models, this setup is most like the simple regression model.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
46
The analysis of variance (ANOVA) technique analyses the variance of the data to determine whether differences exist between the population means.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
47
Conceptually and mathematically, the F-test of the independent-samples single-factor ANOVA is an extension of the t-test of 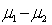 .
.
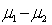 .
.
Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
48
Two samples of 10 each have been taken from the male and female workers of a large company. The data involve the wage rate of each worker. To test whether there is any difference in the average wage rate between male and female workers, a pooled-variances t-test will be considered. Another test option to consider is ANOVA. The most likely ANOVA to fit this test situation is one way ANOVA.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
49
The sum of squares for treatments stands for the between-treatments variation.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
50
When the problem objective is to compare more than two populations, the experimental design that is the counterpart of the matched pairs experiment is called one-way analysis of variance.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
51
In ANOVA, the between-treatments variation is denoted by SST, which stands for sum of squares of treatments.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
52
In one-way ANOVA, the total variation SS(Total) is partitioned into three sources of variation: the sum of squares for treatments (SST), the sum of squares for blocks (SSB) and the sum of squares for error (SSE).

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
53
In ANOVA, a factor is an independent variable.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
54
A study is to be undertaken to examine the effects of two kinds of background music and of two assembly methods on the output of workers at a fitness shoe factory. Two workers will be randomly assigned to each of four groups, for a total of eight in the study. Each worker will be given a headphone set so that the music type can be controlled. The number of shoes completed by each worker will be recorded. Does the kind of music or the assembly method or a combination of music and method affect output? The ANOVA model most likely to fit this situation is the two-way analysis of variance.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
55
In employing the randomised block design, the primary interest lies in reducing the within-treatments variation in order to make easier to detect differences between the treatment means.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
56
In one-way ANOVA, suppose that there are five treatments with 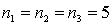 and
and 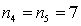 . Then the mean square for error, MSE, equals:
. Then the mean square for error, MSE, equals:
A) SSE / 4.
B) SSE / 29.
C) SSE / 24.
D) SSE / 5.
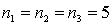 and
and 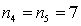 . Then the mean square for error, MSE, equals:
. Then the mean square for error, MSE, equals:A) SSE / 4.
B) SSE / 29.
C) SSE / 24.
D) SSE / 5.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
57
Given the significance level 0.025, the F-value for the numbers of degrees of freedom d.f. = (8, 10) is 3.85.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
58
Three tennis players, one a beginner, one experienced and one a professional, have been randomly selected from the membership of a large city tennis club. Using the same ball, each person hits four serves with each of five racquet models, with the five racquet models selected randomly. Each serve is clocked with a radar gun and the result recorded. Among ANOVA models, this setup is most like the single-factor analysis of variance: independent samples.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
59
We do not need the t-test of 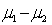 , since the analysis of variance can be used to test the difference between the two population means.
, since the analysis of variance can be used to test the difference between the two population means.
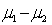 , since the analysis of variance can be used to test the difference between the two population means.
, since the analysis of variance can be used to test the difference between the two population means.
Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
60
The sum of squares for treatments, SST, achieves its smallest value (zero) when all the sample means are equal.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
61
In one-way ANOVA, the test statistic is defined as the ratio of the mean square for treatments (MST), over the mean square for error (MSE)that is, F = MST / MSE.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
62
The distribution of the test statistic for analysis of variance is the F-distribution.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
63
The F-test of the analysis of variance requires that the populations be normally distributed with equal variances.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
64
A randomised block experiment having 5 treatments and 6 blocks produced the following values:
SST = 252, SSB = 1095, SSE = 198. The value of SS(Total) must be 645.
SST = 252, SSB = 1095, SSE = 198. The value of SS(Total) must be 645.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
65
Given the significance level 0.025, the F-value for the numbers of degrees of freedom d.f. = (4, 8) is 5.05.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
66
A survey is to be conducted to compare the superannuation contributions made by employees from three Victorian universities. Employees are to be randomly selected from each of the three universities and the dollar amounts of their contributions recorded. The ANOVA model most likely to fit this situation is the randomised block design.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
67
The sum of squares for treatments (SST) is the variation attributed to the differences between the treatment means, while the sum of squares for error (SSE) measures the variation within the samples.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
68
The F-test of the randomised block design of the analysis of variance has the same requirements as the independent-samples design; that is, the random variable must be normally distributed and the population variances must be equal.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
69
One-way ANOVA is applied to three independent samples having means 12, 15 and 20, respectively. If each observation in the third sample were increased by 40, the value of the F-statistic would increase by 40.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
70
The sum of squares for error (SSE) explains some of the total variation, while the sum of squares for treatments (SST) measures the amount of variation that is unexplained.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
71
The randomised block design is also called the two-way analysis of variance.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
72
The purpose of designing a randomised block experiment is to reduce the between-treatments variation (SST) to more easily detect differences between the treatment means.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
73
A randomised block design with 4 treatments and 5 blocks produced the following sum of squares values: SS(Total) = 2000, SST = 400, SSE = 200. The value of MSB must be 350.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
74
The objective of designing a randomized block experiment is to decrease the within-treatments variation to detect differences between the treatment means.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
75
If we first arrange test units into similar groups before assigning treatments to them, the test design we should use is the randomised block design.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
76
The F-statistic in a one-way ANOVA represents the variation between the treatments divided by the variation within the treatments.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
77
The number of degrees of freedom for the numerator or MST is 3 and that for the denominator or MSE is 18. The total number of observations in the completely randomised design must equal 22.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
78
The sum of squares for treatments, SST, achieves its smallest value (zero) when all the sample sizes are equal.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
79
When the response is not normally distributed, we can replace the randomised block ANOVA with its non-parametric counterpart; the Friedman test.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck
80
The calculated value of F in a one-way analysis is 7.88. The numbers of degrees of freedom for numerator and denominator are 3 and 9, respectively. The most accurate statement to be made about the p-value is that p-value < 0.01.

Unlock Deck
Unlock for access to all 115 flashcards in this deck.
Unlock Deck
k this deck


