Deck 12: Integer Linear Optimization Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/56
Play
Full screen (f)
Deck 12: Integer Linear Optimization Models
1
Which of the following approaches to solving integer linear optimization problems tries to identify the convex hull by adding a series of new constraints that do not exclude any feasible integer points?
A)Branch-and bound approach
B)Cutting plane approach
C)Trial-and-error approach
D)Convex hull approach
A)Branch-and bound approach
B)Cutting plane approach
C)Trial-and-error approach
D)Convex hull approach
Cutting plane approach
2
The ___________ of a set of points is the smallest intersection of linear inequalities that contain the set of points.
A)concave hull
B)slope
C)convex hull
D)geometry
A)concave hull
B)slope
C)convex hull
D)geometry
convex hull
3
In cases where Excel Solver experiences excessive run times when solving integer linear problems, the Integer Optimality is set to
A)5%.
B)0%.
C)infinity.
D)a value equal to the number of integer constraints.
A)5%.
B)0%.
C)infinity.
D)a value equal to the number of integer constraints.
5%.
4
Binary variables are identified with the _____designation in the Solver Parameters dialog box.
A)bin
B)0 and 1
C)int
D)dif
A)bin
B)0 and 1
C)int
D)dif

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
5
The objective function for an optimization problem is: Max 5x - 3y, with constraints x ≥ 0, y ≥ 0 and y must be an integer. x and y are the only decisions variables. This is an example of a(n)
A)all-integer linear program.
B)mixed-integer linear program.
C)LP relaxation of the integer linear program.
D)binary integer linear program.
A)all-integer linear program.
B)mixed-integer linear program.
C)LP relaxation of the integer linear program.
D)binary integer linear program.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
6
The objective function for an optimization problem is: Min 3x - 2y, with constraints x ≥ 0, y ≥ 0. x and y must be integers.. Suppose that the integer restriction on the variables is removed. If so, this would be a familiar two-variable linear program; however, it would also be an example of
A)the convex hull of the linear program.
B)a mixed-integer linear program.
C)an LP relaxation of the integer linear program.
D)a binary integer linear program.
A)the convex hull of the linear program.
B)a mixed-integer linear program.
C)an LP relaxation of the integer linear program.
D)a binary integer linear program.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following is true of the relationship between the value of the optimal integer solution and the value of the optimal solution to the LP Relaxation?
A)For integer linear programs involving minimization, the value of the optimal solution to the LP Relaxation provides an upper bound on the value of the optimal integer solution.
B)For integer linear programs involving maximization, the value of the optimal solution to the LP Relaxation provides a lower bound on the value of the optimal integer solution.
C)For integer linear programs involving minimization, the value of the optimal solution to the LP Relaxation provides a lower bound on the value of the optimal integer solution.
D)For any linear program involving either minimization or maximization, the value of the optimal solution to the LP Relaxation provides an infeasible value for the optimal integer solution.
A)For integer linear programs involving minimization, the value of the optimal solution to the LP Relaxation provides an upper bound on the value of the optimal integer solution.
B)For integer linear programs involving maximization, the value of the optimal solution to the LP Relaxation provides a lower bound on the value of the optimal integer solution.
C)For integer linear programs involving minimization, the value of the optimal solution to the LP Relaxation provides a lower bound on the value of the optimal integer solution.
D)For any linear program involving either minimization or maximization, the value of the optimal solution to the LP Relaxation provides an infeasible value for the optimal integer solution.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
8
The importance of _________ for integer linear programming problems is often intensified by the fact that a small change in one of the coefficients in the constraints can cause a relatively large change in the value of the optimal solution.
A)objective function
B)decision variables
C)sensitivity analysis
D)optimization analysis
A)objective function
B)decision variables
C)sensitivity analysis
D)optimization analysis

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
9
In binary integer linear program, the integer variables take only the values
A)0 or 1.
B)0 or 8.
C)1 or 8.
D)1 or -1.
A)0 or 1.
B)0 or 8.
C)1 or 8.
D)1 or -1.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
10
Which of the following is true about the sensitivity analysis for integer optimization problems?
A)Sensitivity reports are readily available for integer optimization problems similar to the linear programming problems.
B)Because of the discrete nature of the integer optimization, Excel Solver takes much more time to calculate objective function coefficient ranges, shadow prices, and right-hand-side ranges.
C)The sensitivity analysis is not important for integer problems.
D)To determine the sensitivity of the solution to changes in model inputs for integer optimization problems, the data must be changed and the problem must be re-solved.
A)Sensitivity reports are readily available for integer optimization problems similar to the linear programming problems.
B)Because of the discrete nature of the integer optimization, Excel Solver takes much more time to calculate objective function coefficient ranges, shadow prices, and right-hand-side ranges.
C)The sensitivity analysis is not important for integer problems.
D)To determine the sensitivity of the solution to changes in model inputs for integer optimization problems, the data must be changed and the problem must be re-solved.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
11
The objective function for a linear optimization problem is: Max 3x + 5y, with constraints x ≥ 0, y ≥ 0 and x and y are both integers and they are also the only decisions variables. This is an example of a(n)
A)all-integer linear program.
B)mixed-integer linear program.
C)nonlinear program.
D)binary integer linear program.
A)all-integer linear program.
B)mixed-integer linear program.
C)nonlinear program.
D)binary integer linear program.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
12
The imposition of an integer restriction is necessary for models where
A)nonnegativity constraints are needed.
B)variables can take negative values.
C)the decision variables cannot take fractional values.
D)possible values of variables are restricted to particular intervals.
A)nonnegativity constraints are needed.
B)variables can take negative values.
C)the decision variables cannot take fractional values.
D)possible values of variables are restricted to particular intervals.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
13
The objective function for a linear optimization problem is: Max 3x + 2y, with one of the constraints being x and y both only take the values 0, 1. Also x and y are the only decision variables. This is an example of a
A)nonlinear program.
B)mixed-integer linear program.
C)LP relaxation of the integer linear program.
D)binary integer linear program.
A)nonlinear program.
B)mixed-integer linear program.
C)LP relaxation of the integer linear program.
D)binary integer linear program.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
14
__________ is a binary integer programming problem that involves choosing which possible projects or activities provide the best investment return.
A)Capital budgeting problem
B)Fixed-cost problem
C)Market share optimization problem
D)Location problem
A)Capital budgeting problem
B)Fixed-cost problem
C)Market share optimization problem
D)Location problem

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
15
Which of the following is true of rounding the optimized solution of a linear program to an integer?
A)It always produces the most optimal integer solution.
B)It always produces a feasible solution.
C)It does not affect the value of the objective function.
D)It may or may not be feasible.
A)It always produces the most optimal integer solution.
B)It always produces a feasible solution.
C)It does not affect the value of the objective function.
D)It may or may not be feasible.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
16
The optimal solution to the integer linear program will be an extreme point of the
A)convex hull.
B)objective contour.
C)cutting plane.
D)slope.
A)convex hull.
B)objective contour.
C)cutting plane.
D)slope.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
17
The linear program that results from dropping the integer requirements for the variables in an integer linear program is known as
A)convex hull.
B)a mixed-integer linear program.
C)LP relaxation.
D)a binary integer linear program.
A)convex hull.
B)a mixed-integer linear program.
C)LP relaxation.
D)a binary integer linear program.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
18
The ___________ approach to solving integer linear optimization problems breaks the feasible region of the LP Relaxation into subregions until the subregions have integer solutions or it is determined that the solution cannot be in the subregion.
A)cutting plane
B)trial-and-error
C)breaking region
D)branch-and-bound
A)cutting plane
B)trial-and-error
C)breaking region
D)branch-and-bound

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
19
In order to choose the best solution for implementation, practitioners usually recommend re-solving the integer linear program several times with variations in the
A)objective function.
B)decision variables.
C)constraint coefficients.
D)integer constraints.
A)objective function.
B)decision variables.
C)constraint coefficients.
D)integer constraints.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
20
The worksheet formulation for integer linear programs and linear programming problems is exactly the same except that the _____ for integer linear programs.
A)objective function using Set Objective in the Solver Parameters dialog box is set to Value Of option
B)decision variables need not be added in By Changing Variable Cells in the Solver Parameters dialog box
C)decision variables must be added in By Changing Variable Cells in the Solver Parameters dialog box along with selecting the Ignore Integer Constraints in the Integer Options dialog box
D)constraints must be added in the Solver Parameters dialog box to identify the integer variables and the value for Tolerance in the Integer Options dialog box may need to be adjusted
A)objective function using Set Objective in the Solver Parameters dialog box is set to Value Of option
B)decision variables need not be added in By Changing Variable Cells in the Solver Parameters dialog box
C)decision variables must be added in By Changing Variable Cells in the Solver Parameters dialog box along with selecting the Ignore Integer Constraints in the Integer Options dialog box
D)constraints must be added in the Solver Parameters dialog box to identify the integer variables and the value for Tolerance in the Integer Options dialog box may need to be adjusted

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
21
Which of the following is true about generating alternatives in binary optimization?
A)If the second-best solution is very close to optimal, it is always preferred over the true optimal solution because of factors outside the model.
B)If alternative solutions exist, it would not help management because some factors that make one alternative are not preferred over the factors that make another alternative.
C)If the solution is a unique optimal solution, it would be good for management to know how much worse the second-best solution is than the unique optimal solution.
D)If any alternative solution exists, it would only be a second-best next to the optimal solution because there is no third-best or an alternative second-best solution to any binary integer programming problem.
A)If the second-best solution is very close to optimal, it is always preferred over the true optimal solution because of factors outside the model.
B)If alternative solutions exist, it would not help management because some factors that make one alternative are not preferred over the factors that make another alternative.
C)If the solution is a unique optimal solution, it would be good for management to know how much worse the second-best solution is than the unique optimal solution.
D)If any alternative solution exists, it would only be a second-best next to the optimal solution because there is no third-best or an alternative second-best solution to any binary integer programming problem.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
22
In a production application involving a fixed setup cost and a variable cost, the use of ___________ makes including the setup cost possible in a production model.
A)location variables
B)noninteger constraints
C)objective function coefficients
D)binary variables
A)location variables
B)noninteger constraints
C)objective function coefficients
D)binary variables

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
23
Which of the following is a likely constraint on the production quantity x associated with a maximum value and a setup variable y in a fixed-cost problem?
A)x ³ My
B)x £ My
C)Mx £ y
D)xy ³ M
A)x ³ My
B)x £ My
C)Mx £ y
D)xy ³ M

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
24
An apparel designing company is planning to enter the women's trousers market. They are in the process of developing a product that will appeal most to customers. Pink, green, and black will be __________ of the color attribute.
A)levels
B)constraints
C)regression constants
D)utility values
A)levels
B)constraints
C)regression constants
D)utility values

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
25
In a fixed-cost model, each fixed cost is associated with a binary variable and a specification of the
A)upper bound for the corresponding production variable.
B)upper bound for each of the binary variable.
C)integer constraints involving the corresponding production variables.
D)objective function involving these binary variables only.
A)upper bound for the corresponding production variable.
B)upper bound for each of the binary variable.
C)integer constraints involving the corresponding production variables.
D)objective function involving these binary variables only.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
26
For a location problem, if the variables are defined as xi = 1 if an outlet store is established in region i and 0 otherwise, the objective function is best defined by __________ for i = 1, 2, …, n number of outlet stores included in the problem.
A)Min(Sxi)
B)Max(Sxi)
C)Min(pxi)
D)Max(pxi)
A)Min(Sxi)
B)Max(Sxi)
C)Min(pxi)
D)Max(pxi)

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
27
The sum of two or more binary variables must be less than or equal to one in a _____ constraint.
A)corequisite
B)conditional
C)multiple-choice
D)mutually exclusive
A)corequisite
B)conditional
C)multiple-choice
D)mutually exclusive

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
28
An apparel designing company is planning to enter the women's trousers market. They are in the process of developing a product that will appeal most to customers. In an integer programming model for this problem, the available sizes of the trousers will be represented as
A)binary variables
B)constraints
C)attributes
D)regression constants
A)binary variables
B)constraints
C)attributes
D)regression constants

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
29
A constraint involving binary variables that does not allow certain variables to equal one unless certain other variables are equal to one is known as a
A)conditional constraint.
B)corequisite constraint.
C)k out of n alternatives constraint.
D)mutually exclusive constraint.
A)conditional constraint.
B)corequisite constraint.
C)k out of n alternatives constraint.
D)mutually exclusive constraint.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
30
An apparel designing company is planning to enter the women's trousers market. They are in the process of developing a product that will appeal most to customers. What category does the above objective fall under?
A)Capital budgeting problem
B)Covering problem
C)Fixed-cost problem
D)Product design and market share optimization problem
A)Capital budgeting problem
B)Covering problem
C)Fixed-cost problem
D)Product design and market share optimization problem

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
31
Coming up with a product design that will have the highest utility for a sufficient number of people to ensure sufficient sales to justify making the product is known as the ___________ in marketing literature.
A)capital budgeting problem
B)share of choice problem
C)fixed-cost problem
D)traveling-salesman problem
A)capital budgeting problem
B)share of choice problem
C)fixed-cost problem
D)traveling-salesman problem

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
32
An apparel designing company is planning to enter the women's trousers market. They are in the process of developing a product that will appeal most to customers. The part-worths for each of the attribute levels obtained from an initial customer survey and the subsequent regression analysis can be used to determine the
A)customer utility value.
B)optimal solution for the regression analysis.
C)overall profit for the company.
D)overall sales achieved by the company.
A)customer utility value.
B)optimal solution for the regression analysis.
C)overall profit for the company.
D)overall sales achieved by the company.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
33
A binary mixed-integer programming problem in which the binary variables represent whether an activity, such as a production run, is undertaken or not is known as the
A)capital budgeting problem.
B)share of choice problem.
C)fixed-cost problem.
D)covering problem.
A)capital budgeting problem.
B)share of choice problem.
C)fixed-cost problem.
D)covering problem.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
34
_____________ is a market research technique that can be used to learn how prospective buyers of a product value the product's attributes.
A)Part-worth analysis
B)Conjoint analysis
C)Regression analysis
D)Sensitivity analysis
A)Part-worth analysis
B)Conjoint analysis
C)Regression analysis
D)Sensitivity analysis

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
35
In a fixed-cost problem, choosing excessively large values for the maximum production quantity will result in
A)all reasonable levels of production.
B)no production.
C)no solution at all.
D)possibly a slow solution procedure.
A)all reasonable levels of production.
B)no production.
C)no solution at all.
D)possibly a slow solution procedure.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
36
An apparel designing company is planning to enter the women's trousers market. They are in the process of developing a product that will appeal most to customers. The levels - small, medium, and large of the size attribute are modeled using
A)objective function coefficients.
B)slack variables.
C)binary variables.
D)nonlinear coefficients.
A)objective function coefficients.
B)slack variables.
C)binary variables.
D)nonlinear coefficients.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
37
__________ is a constraint requiring that two binary variables be equal and that thus are both either in or out of the solution together.
A)Conditional constraint
B)Corequisite constraint
C)k out of n alternatives constraint
D)Mutually exclusive constraint
A)Conditional constraint
B)Corequisite constraint
C)k out of n alternatives constraint
D)Mutually exclusive constraint

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
38
The part-worth for each of the attribute levels in a conjoint analysis is determined by
A)regression analysis.
B)sensitivity analysis.
C)online surveys.
D)word-of-mouth.
A)regression analysis.
B)sensitivity analysis.
C)online surveys.
D)word-of-mouth.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
39
The results of _____________ can be used in an integer programming model of a product design and market share optimization problem.
A)conjoint analysis
B)product design
C)part-worth
D)variations analysis
A)conjoint analysis
B)product design
C)part-worth
D)variations analysis

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
40
The ___________ is the utility value that a consumer attaches to each level of each attribute in a conjoint analysis model.
A)weightage
B)share of choice
C)part-worth
D)share of market
A)weightage
B)share of choice
C)part-worth
D)share of market

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
41
A shipping freighter has space for two more shipping containers, but the combined weight cannot go over 20 tons. Four shipping containers are being considered. The following table provides details on the weight (in tons) and value of the contents of each container. 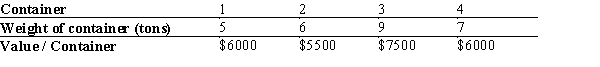
Develop a binary integer model that will determine the two containers that will maximize the value of the shipment.
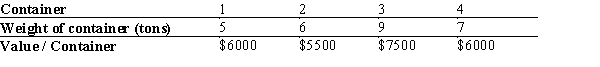
Develop a binary integer model that will determine the two containers that will maximize the value of the shipment.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
42
FinFone Paper Mill is a small-scale paper-making company which produces four different types of paper. Each type of paper must go through processing on four different machines. The manufacturing time (in minutes) per unit of paper produced is listed in the following table. 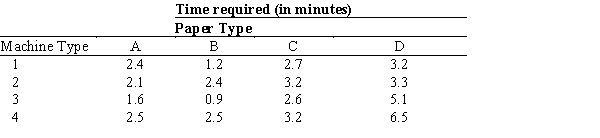
The maximum time allotted for each machine is 30 hours per week and at least 100 units of each type of paper should be made during the week.
Profit per unit is: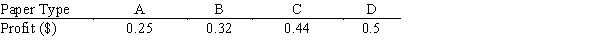
Develop and solve an all-integer model that will determine, using the available machine time, the number of units of each paper type to be produced in order to meet the weekly demand and to maximize the profit.

The maximum time allotted for each machine is 30 hours per week and at least 100 units of each type of paper should be made during the week.
Profit per unit is:
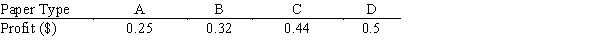
Develop and solve an all-integer model that will determine, using the available machine time, the number of units of each paper type to be produced in order to meet the weekly demand and to maximize the profit.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
43
Sansuit Investments is deciding on future investments for the coming two years and is considering four bonds. The investment details for the next two years are given in the table below. 
The net worth of these four bonds at maturity is $60,000, $40,000, $25,500, and $18,000, respectively. The firm plans to invest $35,000 and $62,000 in Year 1 and Year 2, respectively. Develop and solve a binary integer programming model for maximizing the net worth

The net worth of these four bonds at maturity is $60,000, $40,000, $25,500, and $18,000, respectively. The firm plans to invest $35,000 and $62,000 in Year 1 and Year 2, respectively. Develop and solve a binary integer programming model for maximizing the net worth

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
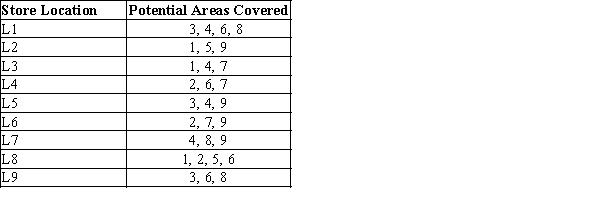
44
To meet excess demand for the pizza home delivery services, ROFiL Pizza is planning to open new stores in various regions. The store locations that are under consideration and their coverage areas are given in the following table.
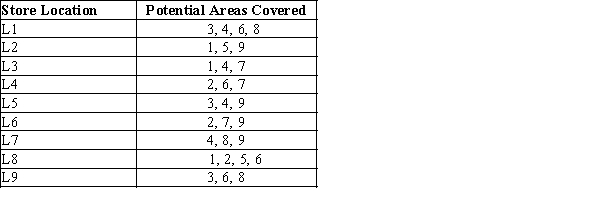
Develop an integer optimization model that determines the minimum number of stores to open in order to meet the coverage demand.

Develop an integer optimization model that determines the minimum number of stores to open in order to meet the coverage demand.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
45
Greenbell Software Inc. conducted a study on its smartphone products in the market to determine which phone has the best features in terms of three prominent attributes: operating system of the phone (A or B), RAM (512MB or 1GB), and the rear camera specifications (3MP, 5MP, or 7MP). A sample of eight customers participated in the study and provided the following part-worths for each of the above attributes.
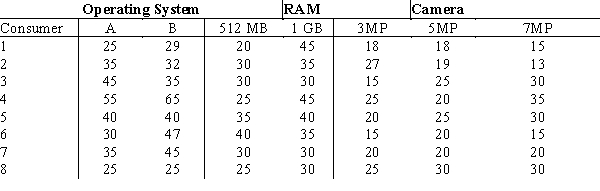 Assume the overall utility (sum of part-worths) of the current favorite Greenbell smartphone for customers 1 to 5 is 105 and customers 6 to 8 is 90. What new product design will maximize the share of choice for the eight consumers in the sample?
Assume the overall utility (sum of part-worths) of the current favorite Greenbell smartphone for customers 1 to 5 is 105 and customers 6 to 8 is 90. What new product design will maximize the share of choice for the eight consumers in the sample?
 Assume the overall utility (sum of part-worths) of the current favorite Greenbell smartphone for customers 1 to 5 is 105 and customers 6 to 8 is 90. What new product design will maximize the share of choice for the eight consumers in the sample?
Assume the overall utility (sum of part-worths) of the current favorite Greenbell smartphone for customers 1 to 5 is 105 and customers 6 to 8 is 90. What new product design will maximize the share of choice for the eight consumers in the sample?
Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
46
A coffee manufacturing company has two processing plants (P1 and P2) that roast imported coffee beans. After roasting, the plants produce three types of coffee beans, A, B, and C. The company has contracted with a chain of cafes to provide coffee beans each week in the following quantities - 20 tons of type A, 11 tons of type B, and 18 tons of type C. The two plants have the same capacity, but their diverse operational procedures affect costs per ton as below.

Formulate and solve the all-integer model that will determine how many tons of each type of coffee beans are produced in each plant while minimizing the total cost.

Formulate and solve the all-integer model that will determine how many tons of each type of coffee beans are produced in each plant while minimizing the total cost.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
47
A manufacturer makes two types of rubber, Butadiene and Polyisoprene. The plant has two machines, Machine-1 and Machine-2, which are used to make the rubber strips. Manufacturing one strip of Butadiene requires 2.75 hours on Machine-1 and 3 hours on Machine-2. Processing one strip of Polyisoprene, takes 3.5 hours on Machine-1 and 4 hours on Machine-2. Machine-1 is available 180 hours per month, and Machine-2 is available 200 hours per month. Formulate an all-integer spreadsheet model that will determine how many units of each type of rubber should be produced to maximize profits if the profit contributions of Butadiene and Polyisoprene are $20 and $26, respectively.
How many units of each type of rubber will maximize profits?
How many units of each type of rubber will maximize profits?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
48
Greenbell Software Inc. conducted a study on its smartphone products in the market to determine which phone has the best features in terms of three prominent attributes: operating system of the phone (A or B), RAM (512MB or 1GB), and the rear camera specifications (3MP, 5MP, or 7MP). A sample of eight customers participated in the study and provided the following part-worths for each of the above attributes.
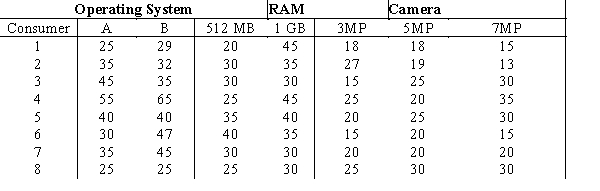 Suppose the overall utility (sum of part-worths) of the current favorite Greenbell smartphone is 100 for each consumer. What new product design will maximize the share of choice for the eight consumers in the sample?
Suppose the overall utility (sum of part-worths) of the current favorite Greenbell smartphone is 100 for each consumer. What new product design will maximize the share of choice for the eight consumers in the sample?
 Suppose the overall utility (sum of part-worths) of the current favorite Greenbell smartphone is 100 for each consumer. What new product design will maximize the share of choice for the eight consumers in the sample?
Suppose the overall utility (sum of part-worths) of the current favorite Greenbell smartphone is 100 for each consumer. What new product design will maximize the share of choice for the eight consumers in the sample?
Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
49
A store is offering a discount on 800 pairs of basketball shoes. The amount of the discount varies and is not revealed to the customer until checkout. The distribution of discounts is given in the below table.
Formulate an integer programming model that could be used to find the minimum number of stores to open in order to cover customers of all areas for the home delivery service.

Formulate an integer programming model that could be used to find the minimum number of stores to open in order to cover customers of all areas for the home delivery service.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
50
A manufacturer wants to construct warehouses in six different locations of the city to supply dry cells to his customers on time. The manufacturer wants to construct the minimum number of warehouses such that each warehouse is within 40 miles of at least one other warehouse. The following table provides the distance (in miles) between the locations. 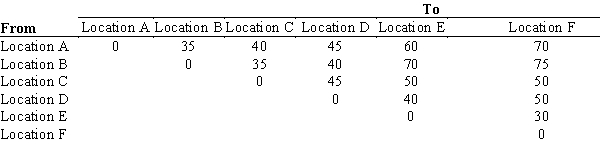 Formulate and solve an integer linear program that can be used to determine the minimum number of warehouses needed to be constructed. What are their locations?
Formulate and solve an integer linear program that can be used to determine the minimum number of warehouses needed to be constructed. What are their locations?
 Formulate and solve an integer linear program that can be used to determine the minimum number of warehouses needed to be constructed. What are their locations?
Formulate and solve an integer linear program that can be used to determine the minimum number of warehouses needed to be constructed. What are their locations?
Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
51
Andrew is ready to invest $200,000 in stocks and he has been provided nine different alternatives by his financial consultant. The following stocks belong to three different industrial sectors and each sector has three varieties of stocks each with different expected rate of return. The average rate of return taken for the past ten years is provided with each of the nine stocks. 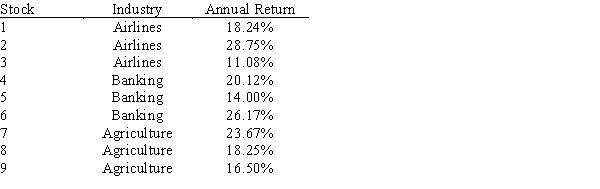
The decision will be based on the constraints provided below:
o Exactly 5 alternatives should be chosen.
o One stock can have a maximum invest of $55,000.
o Any stock chosen must have a minimum investment of at least $25,000.
o For the Airlines sector, the maximum number of stocks chosen should be two.
o The total amount invested in Banking must be at least as much as the amount invested in Agriculture.
Formulate a model that will decide Andrew's investment strategy to maximize his expected annual return.
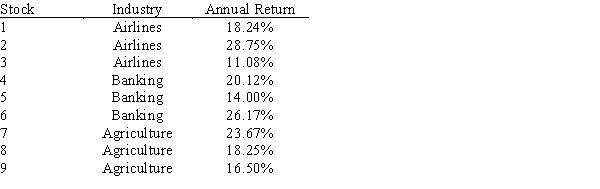
The decision will be based on the constraints provided below:
o Exactly 5 alternatives should be chosen.
o One stock can have a maximum invest of $55,000.
o Any stock chosen must have a minimum investment of at least $25,000.
o For the Airlines sector, the maximum number of stocks chosen should be two.
o The total amount invested in Banking must be at least as much as the amount invested in Agriculture.
Formulate a model that will decide Andrew's investment strategy to maximize his expected annual return.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
52
A chocolate making company largely produces one particular type of crunchy chocolate bar. Only one of two machines, Machine-1 or Machine-2, can be used to produce this chocolate bar on any given day. The maintenance costs incurred on these two machines per day are $100 and $120, respectively. The manufacturing cost per chocolate bar is $2.5 for Machine-1 and $2 for Machine-2. The maximum daily production capacity for Machine-1 and Machine-2 are 1100 and 1250, respectively. Demand requires that at least 1000 chocolate bars be produced per day. Develop and solve an binary integer programming model for minimizing the total cost.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
53
Delisshious Toasty Chocolates Company primarily produces two types of chocolate bars, Almond Tasty and Cashew Crunchy. The personnel costs incurred per day to produce the two types of chocolate bars are $100 and $120, respectively. The production cost per chocolate bar is $2 for Almond Tasty and $2.5 for Cashew Crunchy. The daily production capacity of Almond Tasty and Cashew Crunchy chocolate bars are 1100 and 1250, respectively. Only one type of bar can be produced on a given day since only one machine is available.
Let C1 = the number of Almond Tasty chocolate bars produced
C2 = the number of Cashew Crunchy chocolate bars are produced
Y1 = 1 if the machine produces Almond Tasty; 0, otherwise
Y2 = 1 if the machine produces Cashew Crunchy; 0, otherwise
a. Write a constraint that sets the next day's maximum production of Almond Tasty to 1100.
b. Write a constraint that sets the next day's maximum production of Cashew Crunchy to 1250.
c. Write a constraint that requires that production be set up for exactly one of the two chocolates bars.
d. Write the cost function to be minimized.
Let C1 = the number of Almond Tasty chocolate bars produced
C2 = the number of Cashew Crunchy chocolate bars are produced
Y1 = 1 if the machine produces Almond Tasty; 0, otherwise
Y2 = 1 if the machine produces Cashew Crunchy; 0, otherwise
a. Write a constraint that sets the next day's maximum production of Almond Tasty to 1100.
b. Write a constraint that sets the next day's maximum production of Cashew Crunchy to 1250.
c. Write a constraint that requires that production be set up for exactly one of the two chocolates bars.
d. Write the cost function to be minimized.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
54
A manufacturer makes two types of rubber, Butadiene and Polyisoprene. The plant has two machines, Machine-1 and Machine-2, which are used to make the rubber strips.Manufacturing one strip of Butadiene requires 2.75 hours on Machine-1 and 3 hours on Machine-2. Processing one strip of Polyisoprene, takes 3.5 hours on Machine-1 and 4 hours on Machine-2. Machine-1 is available 180 hours per month, and Machine-2 is available 200 hours per month.Formulate an all-integer mathematical model that will determine how many units of each type of rubber should be produced to maximize profits if the profit contributions of Butadiene and Polyisoprene are $20 and $26, respectively.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
55
Sansuit Investments is deciding on future investment for the coming two years and is considering four bonds. The investment details for the next two years are given in the table below. 
The net worth of these four bonds at maturity is $60,000, $40,000, $25,500, and $18,000, respectively. The firm plans to invest $35,000 and $62,000 in Year 1 and Year 2, respectively.
a. Develop and solve a binary integer programming model for maximizing the return on investment (in dollars) assuming that only one of the bonds can be considered. How much money is invested? What is the return on investment (in dollars)?
b. Suppose the investment has to be made on Bond B, and only two of the four bonds can be considered for investment. Modify your formulation from Part (a) to reflect this new situation. How much money is invested? What is the return on investment (in dollars)? Based on the ratio of return vs. investment, which of these two options would you recommend?

The net worth of these four bonds at maturity is $60,000, $40,000, $25,500, and $18,000, respectively. The firm plans to invest $35,000 and $62,000 in Year 1 and Year 2, respectively.
a. Develop and solve a binary integer programming model for maximizing the return on investment (in dollars) assuming that only one of the bonds can be considered. How much money is invested? What is the return on investment (in dollars)?
b. Suppose the investment has to be made on Bond B, and only two of the four bonds can be considered for investment. Modify your formulation from Part (a) to reflect this new situation. How much money is invested? What is the return on investment (in dollars)? Based on the ratio of return vs. investment, which of these two options would you recommend?

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck
56
Andrew is ready to invest $200,000 in stocks and he has been provided nine different alternatives by his financial consultant. The following stocks belong to three different industrial sectors and each sector has three varieties of stocks each with different expected rate of return. The average rate of return taken for the past ten years is provided with each of the nine stocks. 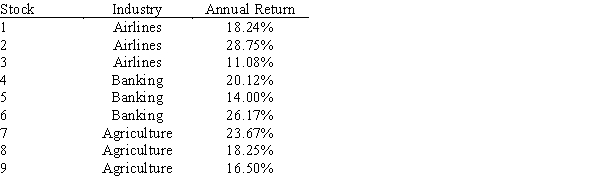
The decision will be based on the constraints provided below:
o Exactly 5 alternatives should be chosen.
o Any stock chosen can have a maximum investment of $55,000.
o Any stock chosen must have a minimum investment of at least $25,000.
o For the Airlines sector, the maximum number of stocks that can be chosen is two.
o The total amount invested in Banking must be at least as much as the amount invested in Agriculture.
Formulate and solve a model that will decide Andrew's investment strategy to maximize his expected annual return.
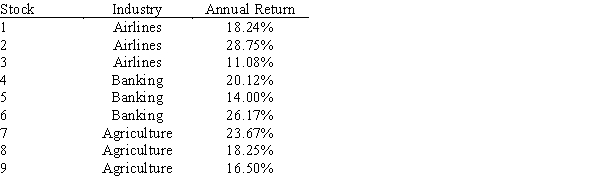
The decision will be based on the constraints provided below:
o Exactly 5 alternatives should be chosen.
o Any stock chosen can have a maximum investment of $55,000.
o Any stock chosen must have a minimum investment of at least $25,000.
o For the Airlines sector, the maximum number of stocks that can be chosen is two.
o The total amount invested in Banking must be at least as much as the amount invested in Agriculture.
Formulate and solve a model that will decide Andrew's investment strategy to maximize his expected annual return.

Unlock Deck
Unlock for access to all 56 flashcards in this deck.
Unlock Deck
k this deck


