Deck 11: Linear Optimization Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/58
Play
Full screen (f)
Deck 11: Linear Optimization Models
1
A ___________ refers to a constraint that can be expressed as an equality at the optimal solution.
A)nonnegativity constraint
B)first class constraint
C)slack variable
D)binding constraint
A)nonnegativity constraint
B)first class constraint
C)slack variable
D)binding constraint
binding constraint
2
In a linear programming model, the __________ assumption plus the nonnegativity constraints mean that decision variables can take on any value greater than or equal to zero.
A)proportionality
B)divisibility
C)additivity
D)negativity
A)proportionality
B)divisibility
C)additivity
D)negativity
divisibility
3
In problem formulation, the
A)objective is expressed in terms of the decision variables.
B)constraints are expressed in terms of the obtained objective function coefficients.
C)nonnegativity constraints are always ignored.
D)optimal solution is decided upon.
A)objective is expressed in terms of the decision variables.
B)constraints are expressed in terms of the obtained objective function coefficients.
C)nonnegativity constraints are always ignored.
D)optimal solution is decided upon.
objective is expressed in terms of the decision variables.
4
A(n) ___________ solution satisfies all the constraint expressions simultaneously.
A)feasible
B)objective
C)infeasible
D)extreme
A)feasible
B)objective
C)infeasible
D)extreme

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
5
Constraints are
A)quantities to be maximized in a linear programming model.
B)quantities to be minimized in a linear programming model.
C)restrictions that limit the settings of the decision variables.
D)input variables that can be controlled during optimization.
A)quantities to be maximized in a linear programming model.
B)quantities to be minimized in a linear programming model.
C)restrictions that limit the settings of the decision variables.
D)input variables that can be controlled during optimization.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
6
The assumption that is necessary for a linear programming model to be appropriate and that ensures that the value of the objective function and the total resources used can be found by summing the objective function contribution and the resources used for all decision variables is known as
A)proportionality.
B)negativity.
C)additivity.
D)divisibility.
A)proportionality.
B)negativity.
C)additivity.
D)divisibility.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
7
The term _____________ refers to the expression that defines the quantity to be maximized or minimized in a linear programming model.
A)objective function
B)problem formulation
C)decision variable
D)association rule
A)objective function
B)problem formulation
C)decision variable
D)association rule

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
8
Which algorithm, developed by George Dantzig and utilized by Excel Solver, is effective at investigating extreme points in an intelligent way to find the optimal solution to even very large linear programs?
A)The ellipsoidal algorithm
B)The complex algorithm
C)The trial-and-error algorithm
D)The simplex algorithm
A)The ellipsoidal algorithm
B)The complex algorithm
C)The trial-and-error algorithm
D)The simplex algorithm

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
9
A mathematical function in which each variable appears in a separate term and is raised to the first power is known as a
A)power function.
B)linear function.
C)what-if function.
D)nonlinear function.
A)power function.
B)linear function.
C)what-if function.
D)nonlinear function.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
10
The points where constraints intersect on the boundary of the feasible region are termed as the
A)feasible points.
B)objective function contour.
C)extreme points.
D)feasible edges.
A)feasible points.
B)objective function contour.
C)extreme points.
D)feasible edges.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
11
A(n) _____________ refers to a set of points that yield a fixed value of the objective function.
A)objective function coefficient
B)infeasible solution
C)objective function contour
D)feasible region
A)objective function coefficient
B)infeasible solution
C)objective function contour
D)feasible region

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
12
The ___________ assumption necessary for a linear programming model to be appropriate, means that the contribution to the objective function and the amount of resources used in each constraint are in accordance to the value of each decision variable.
A)proportionality
B)divisibility
C)additivity
D)negativity
A)proportionality
B)divisibility
C)additivity
D)negativity

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
13
When formulating a constraint, care must be taken to ensure that
A)all the objective function coefficients are included.
B)there are no inequalities in the mathematical expression.
C)the decision variables are set at either maximum or minimum values.
D)the units of measurement on both sides of the constraint match.
A)all the objective function coefficients are included.
B)there are no inequalities in the mathematical expression.
C)the decision variables are set at either maximum or minimum values.
D)the units of measurement on both sides of the constraint match.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
14
A controllable input for a linear programming model is known as a
A)parameter.
B)decision variable.
C)dummy variable.
D)constraint.
A)parameter.
B)decision variable.
C)dummy variable.
D)constraint.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
15
The ___________ value for each less-than-or-equal-to constraint indicates the difference between the left-hand and right-hand values for a constraint.
A)objective function coefficient
B)slack
C)unbounded
D)surplus
A)objective function coefficient
B)slack
C)unbounded
D)surplus

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
16
A variable subtracted from the left-hand side of a greater-than-or-equal to constraint to convert the constraint into an equality is known as a(n)
A)surplus variable.
B)slack variable.
C)unbounded variable.
D)binding constraint.
A)surplus variable.
B)slack variable.
C)unbounded variable.
D)binding constraint.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
17
Suppose that profit for a particular product is calculated using the linear equation: Profit = 20S + 3D. Which of the following combinations of S and D would yield a maximum profit?
A)S = 0, D = 0
B)S = 405, D = 0
C)S = 0, D = 299
D)S = 182, D = 145
A)S = 0, D = 0
B)S = 405, D = 0
C)S = 0, D = 299
D)S = 182, D = 145

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
18
Geometrically, binding constraints intersect to form the
A)subspace.
B)optimal point.
C)decision cell.
D)zero slack.
A)subspace.
B)optimal point.
C)decision cell.
D)zero slack.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
19
The slack value for binding constraints is
A)always a positive integer.
B)zero.
C)a negative integer.
D)equal to the sum of the optimal points in the solution.
A)always a positive integer.
B)zero.
C)a negative integer.
D)equal to the sum of the optimal points in the solution.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
20
_____________ or modeling, is the process of translating a verbal statement of a problem into a mathematical statement.
A)Problem-solving approach
B)Data preparation
C)Data structuring
D)Problem formulation
A)Problem-solving approach
B)Data preparation
C)Data structuring
D)Problem formulation

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
21
Rob is a financial manager with Sharez, an investment advisory company. He must select specific investments-for example, stocks and bonds-from a variety of investment alternatives. Which of the following statements is most likely to be the objective function in this scenario?
A)Minimization of the number of stocks held
B)Maximization of expected return
C)Minimization of tax dues
D)Maximization of investment risk
A)Minimization of the number of stocks held
B)Maximization of expected return
C)Minimization of tax dues
D)Maximization of investment risk

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
22
Gatson manufacturing company produces 2 types of tires: Economy tire; Premium tire. The manufacturing time and the profit contribution per tire are given in the following table.
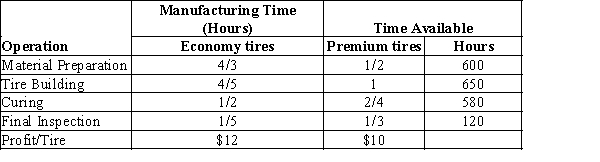 Answer the following assuming that the company is interested in maximizing the total profit contribution.
Answer the following assuming that the company is interested in maximizing the total profit contribution.
a. What is the linear programming model for this problem?
b. Develop a spreadsheet model and find the optimal solution using Excel Solver. How many tires of each model should Gatson manufacture?
c. What is the total profit contribution Gatson can earn with the optimal production quantities?
 Answer the following assuming that the company is interested in maximizing the total profit contribution.
Answer the following assuming that the company is interested in maximizing the total profit contribution. a. What is the linear programming model for this problem?
b. Develop a spreadsheet model and find the optimal solution using Excel Solver. How many tires of each model should Gatson manufacture?
c. What is the total profit contribution Gatson can earn with the optimal production quantities?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
23
The situation in which the value of the solution may be made infinitely large in a maximization linear programming problem or infinitely small in a minimization problem without violating any of the constraints is known as
A)infeasibility.
B)unbounded.
C)infiniteness.
D)semi-optimality.
A)infeasibility.
B)unbounded.
C)infiniteness.
D)semi-optimality.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
24
The change in the optimal objective function value per unit increase in the right-hand side of a constraint is given by the
A)objective function coefficient.
B)shadow price.
C)restrictive cost.
D)allowable increase.
A)objective function coefficient.
B)shadow price.
C)restrictive cost.
D)allowable increase.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
25
Problems with infeasible solutions arise in practice because
A)management doesn't specify enough restrictions.
B)too many restrictions have been placed on the problem.
C)of errors in objective function formulation.
D)there are too few decision variables.
A)management doesn't specify enough restrictions.
B)too many restrictions have been placed on the problem.
C)of errors in objective function formulation.
D)there are too few decision variables.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
26
A canned food manufacturer has its manufacturing plants in three locations across a state. Their product has to be transported to three central distribution centers, which in turn disperse the goods to seventy-two stores across the state. Which of the following visualization tools could help understand this problem better?
A)A time-series plot
B)A scatter chart
C)A network graph
D)A contour plot
A)A time-series plot
B)A scatter chart
C)A network graph
D)A contour plot

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
27
Hire-a-Car System rents three types of cars at two different locations. The profit contribution made per day for each car type at each location is listed below. 
The management forecasts the demand per day by car type as follows: 125 rentals for Economy cars, 55 rentals for Mid-size cars, and 40 rentals for Luxury cars. The vehicle capacity of each location is 100 cars in location A and 120 cars in location B.
Develop a linear programming model to maximize profit and determine how many reservations each location should accept for each type of car. Is the demand for any car type not satisfied? Explain.

The management forecasts the demand per day by car type as follows: 125 rentals for Economy cars, 55 rentals for Mid-size cars, and 40 rentals for Luxury cars. The vehicle capacity of each location is 100 cars in location A and 120 cars in location B.
Develop a linear programming model to maximize profit and determine how many reservations each location should accept for each type of car. Is the demand for any car type not satisfied? Explain.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
28
In linear programming models of real problems, the occurrence of an unbounded solution means that the
A)resultant values of the decision variables have no bounds.
B)mathematical models sufficiently represent the real-world problems.
C)problem formulation is improper.
D)constraints have been excessively used in modeling.
A)resultant values of the decision variables have no bounds.
B)mathematical models sufficiently represent the real-world problems.
C)problem formulation is improper.
D)constraints have been excessively used in modeling.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
29
A scenario in which the optimal objective function contour line coincides with one of the binding constraint lines on the boundary of the feasible region leads to _____ solutions.
A)infeasible
B)alternative optimal
C)binding
D)unique optimal
A)infeasible
B)alternative optimal
C)binding
D)unique optimal

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
30
A canned food manufacturer has its manufacturing plants in three locations across a state. Their product has to be transported to three central distribution centers, which in turn disperse the goods to seventy-two stores across the state. Which of the following is most likely to be the objective function in this scenario?
A)Increasing the number of goods manufactured at the plant
B)Decreasing the cost of their raw material sourcing
C)Minimizing the cost of shipping goods from the plant to the store
D)Minimizing the quantity of goods distributed across the stores
A)Increasing the number of goods manufactured at the plant
B)Decreasing the cost of their raw material sourcing
C)Minimizing the cost of shipping goods from the plant to the store
D)Minimizing the quantity of goods distributed across the stores

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
31
A beverage can manufacturer makes 3 sizes of soft drink cans-Small, Medium and Large. Production is limited by machine availability, with a combined maximum of 90 production hours per day, and the daily supply of metal, no more than 120 kg per day.The following table provides the details of the input needed to manufacture one batch of 100 cans for each size

Develop a linear programming model to maximize profit and determine how many batches of each can size should be produced.

Develop a linear programming model to maximize profit and determine how many batches of each can size should be produced.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
32
Which of the following error messages is displayed in Excel Solver when attempting to solve an unbounded problem?
A)Solver could not find a feasible solution.
B)Solver cannot improve the current solution. All constraints are satisfied.
C)Solver could not find a bounded solution.
D)Objective Cell values do not converge.
A)Solver could not find a feasible solution.
B)Solver cannot improve the current solution. All constraints are satisfied.
C)Solver could not find a bounded solution.
D)Objective Cell values do not converge.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
33
The study of how changes in the input parameters of a linear programming problem affect the optimal solution is known as
A)regression analysis.
B)model analysis.
C)optimality analysis.
D)sensitivity analysis.
A)regression analysis.
B)model analysis.
C)optimality analysis.
D)sensitivity analysis.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
34
Robin Tires, Inc. makes two types of tires, one for SUVs and the other for Hatchbacks.
The firm has the following limits - 500 hours for production, 250 hours for packaging, and 150 hours for shipping.
The times required per tire type is given in the following table.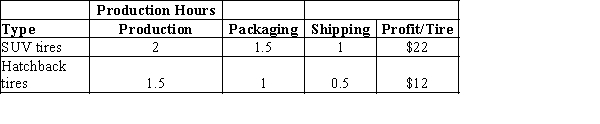
Assuming that the company is interested in maximizing the total profit contribution, answer the following:
a. What is the linear programming model for this problem?
b. Develop a spreadsheet model and find the optimal solution using Excel Solver.How many tires of each model should Robin manufacture?
c. What is the total profit contribution Robin can earn with the optimal production quantities?
The firm has the following limits - 500 hours for production, 250 hours for packaging, and 150 hours for shipping.
The times required per tire type is given in the following table.

Assuming that the company is interested in maximizing the total profit contribution, answer the following:
a. What is the linear programming model for this problem?
b. Develop a spreadsheet model and find the optimal solution using Excel Solver.How many tires of each model should Robin manufacture?
c. What is the total profit contribution Robin can earn with the optimal production quantities?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
35
The reduced cost for a decision variable that appears in a Sensitivity Report refers to the ____________ of the nonnegativity constraint for that variable.
A)range of optimality
B)slack value
C)shadow price
D)range of feasibility
A)range of optimality
B)slack value
C)shadow price
D)range of feasibility

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
36
The reduced cost for a decision variable that appears in a Sensitivity Report indicates the change in the optimal objective function value that results from changing the right-hand side of the nonnegativity constraint from
A)1 to 0.
B)0 to 1.
C)-1 to 0.
D)0 to -1.
A)1 to 0.
B)0 to 1.
C)-1 to 0.
D)0 to -1.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
37
____________ is the situation in which no solution to the linear programming problem satisfies all the constraints.
A)Unboundedness
B)Divisibility
C)Infeasibility
D)Optimality
A)Unboundedness
B)Divisibility
C)Infeasibility
D)Optimality

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
38
Rob is a financial manager with Sharez, an investment advisory company. He must select specific investments-for example, stocks and bonds-from a variety of investment alternatives. Restrictions on the type of permissible investments would be a _________ in this case.
A)feasible solution
B)surplus variable
C)slack variable
D)constraint
A)feasible solution
B)surplus variable
C)slack variable
D)constraint

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
39
The shadow price of nonbinding constraints
A)will always be zero.
B)will always be a positive value.
C)can never be equal to zero.
D)is no longer valid if the right-hand side of the constraint remains the same.
A)will always be zero.
B)will always be a positive value.
C)can never be equal to zero.
D)is no longer valid if the right-hand side of the constraint remains the same.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
40
The supervisor of a manufacturing plant is trying to determine how many of two parts, Part X and Part Y, are to be produced per day. Each part must be processed in three sections of the plant. The time required for the production along with the profit contribution for each part are given in the following table.  No more than 60 units of Part X and up to 70 units of Part Y can be produced per day. The company already has orders for 30 units of Part Y that must be satisfied.
No more than 60 units of Part X and up to 70 units of Part Y can be produced per day. The company already has orders for 30 units of Part Y that must be satisfied.
a. Develop a linear programming model and solve the model to determine the optimal production quantities of Parts X and Y.
b. If more time could be made available in Section 2, how much would the profit increase? (Hint: Generate Answer Report).
 No more than 60 units of Part X and up to 70 units of Part Y can be produced per day. The company already has orders for 30 units of Part Y that must be satisfied.
No more than 60 units of Part X and up to 70 units of Part Y can be produced per day. The company already has orders for 30 units of Part Y that must be satisfied.
a. Develop a linear programming model and solve the model to determine the optimal production quantities of Parts X and Y.
b. If more time could be made available in Section 2, how much would the profit increase? (Hint: Generate Answer Report).

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
41
Three plants P1, P2, and P3 of a gas corporation supply gasoline to three of their distributors in the city located at A, B, and C locations. The plants' daily capacities are 4500, 3000, and 5000, gallons respectively, while the distributors' daily requirements are 5500, 2500, and 4200 gallons. The per-gallon transportation costs (in $) are provided in the table below.

Because of a failure of expected supply earlier, the distributors this time have decided to charge a penalty of $0.45, $0.55, and $0.5 per gallon, respectively for the locations A, B, and C to avoid any further delays.
Find an alternative optimal solution for this transportation problem?

Because of a failure of expected supply earlier, the distributors this time have decided to charge a penalty of $0.45, $0.55, and $0.5 per gallon, respectively for the locations A, B, and C to avoid any further delays.
Find an alternative optimal solution for this transportation problem?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
42
Three plants P1, P2, and P3 of a gas corporation supply gasoline to three of their distributors located in the city at three different locations A, B, and C. The plants' daily capacities are 4500, 3000, and 5000, gallons respectively, while the distributors' daily requirements are 5500, 2500, and 4200 gallons. The per-gallon transportation costs (in $) are provided in the table below.

Because of a failure of expected supply earlier, the distributors - A, B, and C this time have decided to charge a penalty of $0.45, $0.55, and $0.5 per gallon, respectively, to avoid any further delays.
Now, determine the optimum supply of gasoline to the distributors, in order to minimize the total transportation cost as well as the charges payable as penalty.

Because of a failure of expected supply earlier, the distributors - A, B, and C this time have decided to charge a penalty of $0.45, $0.55, and $0.5 per gallon, respectively, to avoid any further delays.
Now, determine the optimum supply of gasoline to the distributors, in order to minimize the total transportation cost as well as the charges payable as penalty.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
43
Robin Tires, Inc. makes two types of tires, one for SUVs and the other for Hatchbacks. The firm has the following limits - 500 hours for production, 250 hours for packaging, and 150 hours for shipping. The times required per tire type is given in the following table 
Assuming that the company is interested in maximizing the total profit contribution, find the optimal solution using Excel Solver and answer the following:
a. How many hours of production time will be scheduled in each department?
b. What is the slack time in each department?
c. If one more hour is available for packaging, what is the change in profit?
d. What is the change in profit if one more hour is available for shipping?

Assuming that the company is interested in maximizing the total profit contribution, find the optimal solution using Excel Solver and answer the following:
a. How many hours of production time will be scheduled in each department?
b. What is the slack time in each department?
c. If one more hour is available for packaging, what is the change in profit?
d. What is the change in profit if one more hour is available for shipping?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
44
Zen Inc. manufactures two types of products, the G.1 and the T.1 models. The manufacturing process consists of two principal departments: production and assembly. The production department has 58 skilled workers, each of whom works 7 hours per day. The assembly department has 25 workers, who also work a 7-hour shift. On an average, to produce a G.1 model, Zen Inc. requires 3.5 labor hours for production and 2 labor hours for assembly. The T.1 model requires 4 labor hours for production and 1.5 labor hours in assembly. The company anticipates selling at least 1.5 times as many T.1 models as G.1 models. The company operates five days per week and makes a net profit of $130 on the G.1 model, and $150 on the T.1 model. Zen Inc. wants to determine how many of each model should be produced on a weekly basis to maximize net profit. Formulate the problem.
Let the number of G.1 product produced each week be G
Let the number of T.1 product produced each week be T
Maximize 130G + 150T
s.t.
production's labor constraint 3.5G + 4T <= 2030
assembly's labor constraint 2G + 1.5T <= 875
Let the number of G.1 product produced each week be G
Let the number of T.1 product produced each week be T
Maximize 130G + 150T
s.t.
production's labor constraint 3.5G + 4T <= 2030
assembly's labor constraint 2G + 1.5T <= 875

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
45
A soft drink manufacturing company has 3 factories-one in Orlando, one in Tampa, and one in Port St. Lucie-which supply soft drink bottles to 3 warehouses located in the city of Miami. The associated per-unit transportation cost table is provided below.  The factory in Orlando has a capacity of 15,000 units.
The factory in Orlando has a capacity of 15,000 units.
The factory in Tampa has a capacity of 18,000 units.
The factory in Port St. Lucie has a capacity of 8,000 units.
The requirements of the warehouses are:
a. Determine how much of the company's production should be shipped from each factory to each warehouse in order to minimize the total transportation cost?
b. Find an alternative optimal solution for this transportation problem?
 The factory in Orlando has a capacity of 15,000 units.
The factory in Orlando has a capacity of 15,000 units.The factory in Tampa has a capacity of 18,000 units.
The factory in Port St. Lucie has a capacity of 8,000 units.
The requirements of the warehouses are:

a. Determine how much of the company's production should be shipped from each factory to each warehouse in order to minimize the total transportation cost?
b. Find an alternative optimal solution for this transportation problem?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
46
Two mining fields, Field A and Field B, of a coal mining company produce Lignite and Bituminous coal. The operating cost per day for Field A and Field B are $55,000 and $45,000, respectively.The recent records at the company indicate that Field A can produce 250 tons of Lignite along with 300 tons of Bituminous coal per day, whereas Field B can produce 200 tons of Lignite along with 450 tons of Bituminous coal per day. The expected demands to be met are 120,000 tons of Lignite and 170,000 tons of Bituminous coal. To minimize the operating costs of the mining fields, how many days does the company need to operate each of these fields?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
47
A company has three treatments that it can apply three different types of clothes namely denims, linens and suiting yielding the profit $4, $5, and $8 per bolt respectively. One bolt of denims requires 2 hours in Treatment 1, 3 hours in Treatment 2 and 4 hours in Treatment 3. Similarly one bolt of linens requires 3 hours in Treatment 1, 2 hours in Treatment 2 and 4 hours in Treatment 3 while one bolt suiting requires 2 hours in Treatment 1, 3 hours in Treatment 2 and 4 hours in Treatment 3. In a week, total run time of each department is 80 hours, 90 hours, and 65 hours for Treatment 1, Treatment 2 and Treatment 3 respectively.
Formulation
Let
D1 number of bolts of denims with Treatment 1
D2 number of bolts of denims with Treatment 2
D3 number of bolts of denims with Treatment 3
.
.
.
S3 number of bolts of Suiting with Treatment 3
Max $4(DW + DI + DP) + $5(LW + LI + LP) +$8(SW + SI + SP)
s.t.
2D1 + 3L1 + 3S1 ≤ 80
3D2 + 2L2 + 3S2 ≤ 90
4D3 + 4L3 + 3S3 ≤ 65
D1, D2, D3, …, S3 ≥ 0
Formulation
Let
D1 number of bolts of denims with Treatment 1
D2 number of bolts of denims with Treatment 2
D3 number of bolts of denims with Treatment 3
.
.
.
S3 number of bolts of Suiting with Treatment 3
Max $4(DW + DI + DP) + $5(LW + LI + LP) +$8(SW + SI + SP)
s.t.
2D1 + 3L1 + 3S1 ≤ 80
3D2 + 2L2 + 3S2 ≤ 90
4D3 + 4L3 + 3S3 ≤ 65
D1, D2, D3, …, S3 ≥ 0

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
48
Michael has decided to invest $40,000 in three types of funds. Fund A has projected an annual return of 8 percent, Fund B has projected an annual return of 10 percent, and Fund C has projected an annual return of 9 percent. He has decided to invest no more than 30 percent of the total amount in Fund B and no more than 40 percent of the total amount in Fund C.
a. Formulate a linear programming model that can be used to determine the amount of investments Michael should allocate to each type of fund to maximize the total annual return.
b. How much should be allocated to each type of fund? What is the total annual return?
a. Formulate a linear programming model that can be used to determine the amount of investments Michael should allocate to each type of fund to maximize the total annual return.
b. How much should be allocated to each type of fund? What is the total annual return?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
49
Ethan Steel, Inc. has two factories that manufacture steel components for four different rail projects. The demand for the steel components for the four projects, Project A, Project B, Project C, and Project D, are 3220, 3675, 4125, and 2975, respectively. The shipping details are as below:
Production details:
Shipping Details (with per-unit shipping cost): Find an alternative optimal solution for this transportation problem?
Find an alternative optimal solution for this transportation problem?
Production details:

Shipping Details (with per-unit shipping cost):
 Find an alternative optimal solution for this transportation problem?
Find an alternative optimal solution for this transportation problem?
Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
50
Northwest California Ventures Ltd. has decided to provide capital in five market areas for the start-ups. The investment consultant for the venture capital company has projected an annual rate of return based on the market risk, the product, and the size of the market.

The maximum capital provided will be $5 million.
The consultant has imposed conditions on allotment of capital based on the risk involved in the market.
• The capital provided to retail should be at most 40 percent of the total capital.
• The capital for education should be 26 percent of the total of other four markets (Electronics, Software, Logistics, and Retail)
• Logistics should be at least 15 percent of the total capital.
• The capital allocated for Software plus Logistics should be no more than the capital allotted for Electronics.
• The capital allocated for Logistics plus Education should not be greater than that allocated to Retail.
Calculate the expected annual rate of return based on the allocation of capital to each market area to maximize the return on capital provided. Also, show the allocation of capital for each market area.

The maximum capital provided will be $5 million.
The consultant has imposed conditions on allotment of capital based on the risk involved in the market.
• The capital provided to retail should be at most 40 percent of the total capital.
• The capital for education should be 26 percent of the total of other four markets (Electronics, Software, Logistics, and Retail)
• Logistics should be at least 15 percent of the total capital.
• The capital allocated for Software plus Logistics should be no more than the capital allotted for Electronics.
• The capital allocated for Logistics plus Education should not be greater than that allocated to Retail.
Calculate the expected annual rate of return based on the allocation of capital to each market area to maximize the return on capital provided. Also, show the allocation of capital for each market area.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
51
Ethan Steel, Inc. has two factories that manufacture steel components for four different rail projects. The demand for the steel components for the four projects, Project A, Project B, Project C, and Project D, are 3220, 3675, 4125, and 2975, respectively. The shipping details are as below.
Production Details:
Shipping Details (with per-unit shipping cost): What is the optimal (cost minimizing) distribution plan for this transportation problem?
What is the optimal (cost minimizing) distribution plan for this transportation problem?
Production Details:

Shipping Details (with per-unit shipping cost):
 What is the optimal (cost minimizing) distribution plan for this transportation problem?
What is the optimal (cost minimizing) distribution plan for this transportation problem?
Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
52
Sunseel Industries produces two types of raw materials, A and B, with a production cost of $4 and $8 per unit, respectively. The combined production of A and B must be at least 700 units per month. The factory is expected to produce at least 400 units of B and not more than 1200 units of A each month. The processing times for A and B are observed to be 5 hours and 4 hours, respectively. A total of 3000 production hours are available per month.. Develop a linear program that Sunseel Industries can use to determine the number of units of each raw material to produce that will meet the demand and minimize the total cost.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
53
Zen Inc. manufactures two types of products, the G.1 and the T.1 models. The manufacturing process consists of two principal departments: production and assembly. The production department has 58 skilled workers, each of whom works 7 hours per day. The assembly department has 25 workers, who also work a 7-hour shift. On an average, to produce a G.1 model, Zen Inc. requires 3.5 labor hours for production and 2 labor hours for assembly. The T.1 model requires 4 labor hours for production and 1.5 labor hours in assembly. The company anticipates selling at least 1.5 times as many T.1 models as G.1 models. The company operates five days per week and makes a net profit of $130 on the G.1 model, and $150 on the T.1 model. Zen Inc. wants to determine how many of each model should be produced on a weekly basis to maximize net profit. Solve Using the Excel Solver tool.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
54
Zen Inc. manufactures two types of products, the G.1 and the T.1 models. The manufacturing process consists of two principal departments: production and assembly. The production department has 58 skilled workers, each of whom works 7 hours per day. The assembly department has 25 workers, who also work a 7-hour shift. On an average, to produce a G.1 model, Zen Inc. requires 3.5 labor hours for production and 2 labor hours for assembly. The T.1 model requires 4 labor hours for production and 1.5 labor hours in assembly. The company anticipates selling at least 1.5 times as many T.1 models as G.1 models. The company operates five days per week and makes a net profit of $130 on the G.1 model, and $150 on the T.1 model. Zen Inc. wants to determine how many of each model should be produced on a weekly basis to maximize net profit. What is the projected profit at the maximized number of units produced?
Let the number of G.1 product produced each week be G
Let the number of T.1 product produced each week be T
Maximize 130G + 150T
production's labor constraint 3.5G + 4T <= 2030
assembly's labor constraint 2G + 1.5T <= 875
Let the number of G.1 product produced each week be G
Let the number of T.1 product produced each week be T
Maximize 130G + 150T
production's labor constraint 3.5G + 4T <= 2030
assembly's labor constraint 2G + 1.5T <= 875

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
55
The Pat-A-Cake Pastry Shop makes chocolate cake in three sizes - Small, Medium, and Large. The shop has the following amounts of the three main ingredients on hand - 400 ounces of cake flour, 550 ounces of caster sugar, and 150 ounces of cocoa powder. The table below provides details on the amount of each ingredient required for each cake size as well as the profit contributions.  Develop and solve a linear programming model to maximize the profit. What is the optimal solution for this problem?
Develop and solve a linear programming model to maximize the profit. What is the optimal solution for this problem?
 Develop and solve a linear programming model to maximize the profit. What is the optimal solution for this problem?
Develop and solve a linear programming model to maximize the profit. What is the optimal solution for this problem?
Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
56
Clever Sporting Equipment, Inc. makes two types of balls: Soccer balls and Cork balls. The making of each soccer ball and cork ball requires 3 hours and 4 hours of production time, respectively. A total of 500 production hours are available during the next month At least 150 balls, combined, must be produced. The production cost for each Soccer ball is $9 and each Cork ball is $7. Develop a linear programming model to minimize production costs and determine how many of each type of ball should be produced to meet the required demand.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
57
Jackson just obtained $240,000 by selling mutual funds and is now looking for other investment opportunities for these funds. His financial consultant recommends that all new investments be made in the stocks of industries such as Agriculture, Healthcare, Banking, Manufacturing, and Real Estate. The projected annual rates of returns for the investments are as follows:
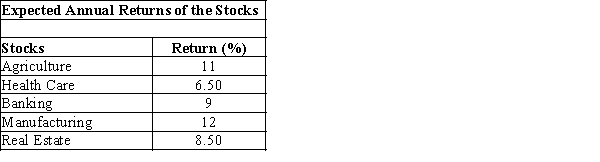
His consultant has set constraints on the investments based on the calculated risks involved with the industries:
1) Neither Agriculture nor Manufacturing should receive more than $100,000.
2) Neither Healthcare nor Banking should receive more than $50,000.
3) The amount invested in Manufacturing should not be more than 45 percent of the sum of the investment in Banking and Healthcare sectors.
4) The amount invested in Real Estate should be at least 20 percent of the sum of the investment in Banking and Healthcare sectors.
Develop portfolio recommendations-investments and amounts-for investing the available $240,000.

His consultant has set constraints on the investments based on the calculated risks involved with the industries:
1) Neither Agriculture nor Manufacturing should receive more than $100,000.
2) Neither Healthcare nor Banking should receive more than $50,000.
3) The amount invested in Manufacturing should not be more than 45 percent of the sum of the investment in Banking and Healthcare sectors.
4) The amount invested in Real Estate should be at least 20 percent of the sum of the investment in Banking and Healthcare sectors.
Develop portfolio recommendations-investments and amounts-for investing the available $240,000.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
58
A soft drink manufacturing company has 3 factories-one in Orlando, one in Tampa, and one in Port St. Lucie-which supply soft drink bottles to 3 warehouses located in the city of Miami. The associated per-unit transportation cost between the factories and the warehouses is provided in the table below.
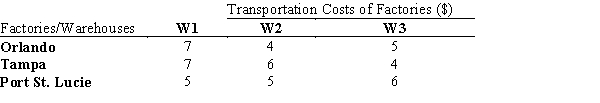 The factory in Orlando has a capacity of 14,000 units.
The factory in Orlando has a capacity of 14,000 units.
The factory in Tampa has a capacity of 25,000 units.
The factory in Port St. Lucie has a capacity of 23,000 units.
The requirements of the warehouses are:
Determine how much of the company's production should be shipped from each factory to each warehouse in order to minimize the total transportation cost?
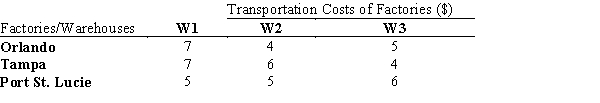 The factory in Orlando has a capacity of 14,000 units.
The factory in Orlando has a capacity of 14,000 units.The factory in Tampa has a capacity of 25,000 units.
The factory in Port St. Lucie has a capacity of 23,000 units.
The requirements of the warehouses are:

Determine how much of the company's production should be shipped from each factory to each warehouse in order to minimize the total transportation cost?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck


