Deck 4: Introduction to Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/99
Play
Full screen (f)
Deck 4: Introduction to Probability
1
The collection of all possible sample points in an experiment is
A) the sample space.
B) an event.
C) a combination.
D) the population.
A) the sample space.
B) an event.
C) a combination.
D) the population.
the sample space.
2
Two events are mutually exclusive
A) if their intersection is 1.
B) if they have no sample points in common.
C) if their intersection is 0.5.
D) if most of their sample points are in common.
A) if their intersection is 1.
B) if they have no sample points in common.
C) if their intersection is 0.5.
D) if most of their sample points are in common.
if they have no sample points in common.
3
Each individual outcome of an experiment is called
A) the sample space.
B) a sample point.
C) a trial.
D) an event.
A) the sample space.
B) a sample point.
C) a trial.
D) an event.
a sample point.
4
In statistical experiments, each time the experiment is repeated
A) the same outcome must occur.
B) the same outcome can not occur again.
C) a different outcome might occur.
D) a different out come must occur.
A) the same outcome must occur.
B) the same outcome can not occur again.
C) a different outcome might occur.
D) a different out come must occur.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
5
Initial estimates of the probabilities of events are known as _____ probabilities.
A) subjective
B) posterior
C) conditional
D) prior
A) subjective
B) posterior
C) conditional
D) prior

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
6
The counting rule that is used for counting the number of experimental outcomes when n objects are selected from a set of N objects where order of selection is not important is called the rule for
A) permutations.
B) combinations.
C) independent events.
D) multiple-step experiments.
A) permutations.
B) combinations.
C) independent events.
D) multiple-step experiments.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
7
Events that have no sample points in common are
A) independent events.
B) supplements.
C) mutually exclusive events.
D) complements.
A) independent events.
B) supplements.
C) mutually exclusive events.
D) complements.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
8
An experiment consists of selecting a student body president and vice president.All undergraduate students (freshmen through seniors) are eligible for these offices.How many sample points (possible outcomes as to the classifications) exist?
A) 4
B) 16
C) 8
D) 32
A) 4
B) 16
C) 8
D) 32

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
9
When the results of experimentation or historical data are used to assign probability values, the method used to assign probabilities is referred to as the _____ method.
A) relative frequency
B) subjective
C) classical
D) posterior
A) relative frequency
B) subjective
C) classical
D) posterior

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
10
Which of the following statements is always true?
A) -1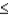 P(Ei)
P(Ei) 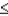 1
1
B) P(A) = 1 - P(Ac)
C) P(A) + P(B) = 1
D) ∑P 1
1
A) -1
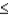 P(Ei)
P(Ei) 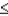 1
1B) P(A) = 1 - P(Ac)
C) P(A) + P(B) = 1
D) ∑P
 1
1
Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
11
Any process that generates well-defined outcomes is a(n)
A) event.
B) experiment.
C) sample point.
D) sample space.
A) event.
B) experiment.
C) sample point.
D) sample space.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
12
From a group of six people, two individuals are to be selected at random.How many selections are possible?
A) 12
B) 36
C) 15
D) 8
A) 12
B) 36
C) 15
D) 8

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
13
The intersection of two mutually exclusive events
A) can be any value between 0 to1.
B) must always be equal to 1.
C) must always be equal to 0.
D) can be any positive value.
A) can be any value between 0 to1.
B) must always be equal to 1.
C) must always be equal to 0.
D) can be any positive value.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
14
A method of assigning probabilities based upon judgment is referred to as the _____ method.
A) relative
B) probability
C) classical
D) subjective
A) relative
B) probability
C) classical
D) subjective

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
15
The range of probability values is
A) 0 to infinity.
B) minus infinity to plus infinity.
C) 0 to 1.
D) -1 to 1.
A) 0 to infinity.
B) minus infinity to plus infinity.
C) 0 to 1.
D) -1 to 1.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
16
Two events with nonzero probabilities
A) can be both mutually exclusive and independent.
B) can not be both mutually exclusive and independent.
C) are always mutually exclusive.
D) are always independent.
A) can be both mutually exclusive and independent.
B) can not be both mutually exclusive and independent.
C) are always mutually exclusive.
D) are always independent.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
17
The sample space refers to
A) any particular experimental outcome.
B) the sample size minus one.
C) the set of all possible experimental outcomes.
D) an event.
A) any particular experimental outcome.
B) the sample size minus one.
C) the set of all possible experimental outcomes.
D) an event.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
18
A graphical method of representing the sample points of an experiment is a
A) stacked bar chart.
B) dot plot.
C) stem-and-leaf display.
D) tree diagram.
A) stacked bar chart.
B) dot plot.
C) stem-and-leaf display.
D) tree diagram.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
19
The counting rule that is used for counting the number of experimental outcomes when n objects are selected from a set of N objects where order of selection is important is called the counting rule for
A) permutations.
B) combinations.
C) independent events.
D) multiple-step random experiments.
A) permutations.
B) combinations.
C) independent events.
D) multiple-step random experiments.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
20
When the assumption of equally likely outcomes is used to assign probability values, the method used to assign probabilities is referred to as the _____ method.
A) relative frequency
B) subjective
C) probability
D) classical
A) relative frequency
B) subjective
C) probability
D) classical

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
21
Four applications for admission to a local university are checked, and it is determined whether each applicant is male or female.The number of sample points in this experiment is
A) 2.
B) 4.
C) 16.
D) 8.
A) 2.
B) 4.
C) 16.
D) 8.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
22
The symbol ∪ shows the
A) union of events.
B) intersection of two events.
C) sum of the probabilities of events.
D) sample space.
A) union of events.
B) intersection of two events.
C) sum of the probabilities of events.
D) sample space.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
23
Bayes' theorem is used to compute
A) the prior probabilities.
B) the union of events.
C) intersection of events.
D) the posterior probabilities.
A) the prior probabilities.
B) the union of events.
C) intersection of events.
D) the posterior probabilities.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
24
If two events are independent, then
A) they must be mutually exclusive.
B) the sum of their probabilities must be equal to one.
C) their intersection must be zero.
D) the product of their probabilities gives their intersection.
A) they must be mutually exclusive.
B) the sum of their probabilities must be equal to one.
C) their intersection must be zero.
D) the product of their probabilities gives their intersection.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
25
If a penny is tossed three times and comes up heads all three times, the probability of heads on the fourth trial is
A) 0.
B) 1/16.
C) 1/2.
D) larger than the probability of tails.
A) 0.
B) 1/16.
C) 1/2.
D) larger than the probability of tails.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
26
Assuming that each of the 52 cards in an ordinary deck has a probability of 1/52 of being drawn, what is the probability of drawing a black card?
A) 1/52
B) 4/52
C) 13/52
D) 26/52
A) 1/52
B) 4/52
C) 13/52
D) 26/52

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
27
The addition law is potentially helpful when we are interested in computing the probability of
A) independent events
B) the intersection of two events
C) the union of two events
D) conditional events
A) independent events
B) the intersection of two events
C) the union of two events
D) conditional events

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
28
If P(A) = 0.4, P(B | A) = 0.35, P(A ∪ B) = 0.69, then P(B) =
A) 0.14.
B) 0.43.
C) 0.75.
D) 0.59.
A) 0.14.
B) 0.43.
C) 0.75.
D) 0.59.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
29
The union of events A and B is the event containing all the sample points belonging to
A) B or A.
B) A or B.
C) A or B or both.
D) A or B, but not both.
A) B or A.
B) A or B.
C) A or B or both.
D) A or B, but not both.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
30
If A and B are independent events with P(A) = 0.5 and P(A ∩ B) = 0.12, then, P(B) =
A) 0.240.
B) 0.060.
C) 0.380.
D) 0.620.
A) 0.240.
B) 0.060.
C) 0.380.
D) 0.620.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
31
The symbol ∩ shows the
A) union of events.
B) intersection of two events.
C) sum of the probabilities of events.
D) sample space.
A) union of events.
B) intersection of two events.
C) sum of the probabilities of events.
D) sample space.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
32
The set of all possible outcomes of an experiment is
A) a sample point.
B) an event.
C) the population.
D) the sample space.
A) a sample point.
B) an event.
C) the population.
D) the sample space.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
33
The multiplication law is potentially helpful when we are interested in computing the probability of
A) mutually exclusive events.
B) the intersection of two events.
C) the union of two events.
D) conditional events.
A) mutually exclusive events.
B) the intersection of two events.
C) the union of two events.
D) conditional events.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
34
An experiment consists of three steps.There are five possible results on the first step, two possible results on the second step, and three possible results on the third step.The total number of experimental outcomes is
A) 10.
B) 625.
C) 150.
D) 180.
A) 10.
B) 625.
C) 150.
D) 180.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
35
Assume your favorite soccer team has 4 games left to finish the season.The outcome of each game can be win, lose or tie.The number of possible outcomes is
A) 4.
B) 12.
C) 64.
D) 81.
A) 4.
B) 12.
C) 64.
D) 81.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
36
Of six letters (A, B, C, D, E, and F), two letters are to be selected at random.How many outcomes are possible?
A) 30
B) 11
C) 6!
D) 15
A) 30
B) 11
C) 6!
D) 15

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
37
The sum of the probabilities of two complementary events is
A) 0.
B) 0.5.
C) 0.57.
D) 1.0.
A) 0.
B) 0.5.
C) 0.57.
D) 1.0.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
38
Each customer entering a department store will either buy or not buy some merchandise.An experiment consists of following 5 customers and determining whether or not they purchase any merchandise.The number of sample points in this experiment is
A) 5.
B) 10.
C) 25.
D) 64.
A) 5.
B) 10.
C) 25.
D) 64.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
39
An experiment consists of tossing 4 coins successively.The number of sample points in this experiment is
A) 16.
B) 8.
C) 4.
D) 2.
A) 16.
B) 8.
C) 4.
D) 2.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
40
If a six sided die is tossed two times and "3" shows up both times, the probability of "3" on the third trial is
A) much larger than any other outcome.
B) much smaller than any other outcome.
C) the same as any other outcome.
D) not able to be determined before the die is tossed.
A) much larger than any other outcome.
B) much smaller than any other outcome.
C) the same as any other outcome.
D) not able to be determined before the die is tossed.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
41
An experiment consists of four outcomes with P(E1) = 0.2, P(E2) = 0.25, and P(E3) = 0.05.The probability of outcome E4 is
A) 0.500.
B) 0.0025.
C) 0.100.
D) 0.
A) 0.500.
B) 0.0025.
C) 0.100.
D) 0.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
42
Events A and B are mutually exclusive.Which of the following statements is also true?
A) A and B are also independent.
B) P(A ∪ B) = P(A)P(B)
C) P(A ∪ B) = P(A) + P(B)
D) P(A ∩ B) = P(A) + P(B)
A) A and B are also independent.
B) P(A ∪ B) = P(A)P(B)
C) P(A ∪ B) = P(A) + P(B)
D) P(A ∩ B) = P(A) + P(B)

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
43
If P(A) = 0.58, P(B) = 0.44, and P(A ∩ B) = 0.25, then P(A ∪ B) =
A) 1.02.
B) 0.77.
C) 0.11.
D) 0.39.
A) 1.02.
B) 0.77.
C) 0.11.
D) 0.39.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
44
A six-sided die is tossed 4times.The probability of observing four ones in a row is
A) 4/6.
B) 1/6.
C) 1/4096.
D) 1/1296.
A) 4/6.
B) 1/6.
C) 1/4096.
D) 1/1296.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
45
Of the last 100 customers entering a computer shop, 40have purchased a computer.If the classical method for computing probability is used, the probability that the next customer will purchase a computer is
A) 0.40.
B) 0.50.
C) 1.00.
D) 0.60.
A) 0.40.
B) 0.50.
C) 1.00.
D) 0.60.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
46
If A and B are independent events with P(A) = 0.5 and P(B) = 0.5, then P(A ∩ B) is
A) 0.00.
B) 1.00.
C) 0.5.
D) 0.25.
A) 0.00.
B) 1.00.
C) 0.5.
D) 0.25.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
47
The probability of the occurrence of event A in an experiment is 1/3.If the experiment is performed 2 times and event A did not occur, then on the third trial event A
A) must occur.
B) may occur.
C) could not occur.
D) has a 2/3 probability of occurring.
A) must occur.
B) may occur.
C) could not occur.
D) has a 2/3 probability of occurring.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
48
Events A and B are mutually exclusive with P(C) = 0.35 and P(B) = 0.25.Then, P(Bc) =
A) 0.62.
B) 0.50.
C) 0.75.
D) 0.60.
A) 0.62.
B) 0.50.
C) 0.75.
D) 0.60.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
49
A method of assigning probabilities which assumes that the experimental outcomes are equally likely is referred to as the _____ method.
A) objective
B) classical
C) subjective
D) experimental
A) objective
B) classical
C) subjective
D) experimental

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
50
If A and B are mutually exclusive events with P(A) = 0.25 and P(B) = 0.4, then P(A ∪ B) =
A) 0.
B) 0.15.
C) 0.1.
D) 0.65.
A) 0.
B) 0.15.
C) 0.1.
D) 0.65.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
51
If A and B are independent events with P(A) = 0.2 and P(B) = 0.6, then P(A ∪ B) =
A) 0.62.
B) 0.12.
C) 0.60.
D) 0.68.
A) 0.62.
B) 0.12.
C) 0.60.
D) 0.68.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
52
In an experiment, events A and B are mutually exclusive.If P(A) = 0.6, then the probability of B
A) cannot be larger than 0.4.
B) can be any value greater than 0.6.
C) can be any value between 0 to 1.
D) cannot be determined with the information given.
A) cannot be larger than 0.4.
B) can be any value greater than 0.6.
C) can be any value between 0 to 1.
D) cannot be determined with the information given.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
53
If A and B are independent events with P(A) = 0.05 and P(B) = 0.65, then P(A ∩ B) =
A) 0.05.
B) 0.0325.
C) 0.65.
D) 0.8.
A) 0.05.
B) 0.0325.
C) 0.65.
D) 0.8.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
54
A lottery is conducted using four urns.Each urn contains chips numbered from 0 to 9.One chip is selected at random from each urn.The total number of sample points in the sample space is
A) 40.
B) 6,561.
C) 1,048,576.
D) 10,000.
A) 40.
B) 6,561.
C) 1,048,576.
D) 10,000.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
55
If A and B are mutually exclusive events with P(A) = 0.3 and P(B) = 0.5, then P(A ∩ B) =
A) 0.30.
B) 0.15.
C) 0.00.
D) 0.20.
A) 0.30.
B) 0.15.
C) 0.00.
D) 0.20.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
56
If a coin is tossed three times, the likelihood of obtaining three heads in a row is
A) 0.0.
B) 0.500.
C) 0.875.
D) 0.125.
A) 0.0.
B) 0.500.
C) 0.875.
D) 0.125.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
57
A method of assigning probabilities based on historical data is called the _____ method.
A) classical
B) subjective
C) relative frequency
D) progressive
A) classical
B) subjective
C) relative frequency
D) progressive

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
58
A perfectly balanced coin is tossed 6 times, and tails appears on all six tosses.Then, on the seventh trial
A) tail can not appear.
B) head has a larger chance of appearing than tail.
C) tail has a better chance of appearing than head.
D) tail has same chance of appearing as the head.
A) tail can not appear.
B) head has a larger chance of appearing than tail.
C) tail has a better chance of appearing than head.
D) tail has same chance of appearing as the head.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
59
If A and B are independent events with P(A) = 0.4 and P(B) = 0.25, then P(A ∩ B) =
A) 0.65.
B) 0.1.
C) 0.625.
D) 0.15.
A) 0.65.
B) 0.1.
C) 0.625.
D) 0.15.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
60
If P(A) = 0.62, P(B) = 0.47, and P(A ∪ B) = 0.88, then P(A ∩ B) =
A) 0.2914.
B) 1.9700.
C) 0.6700.
D) 0.2100.
A) 0.2914.
B) 1.9700.
C) 0.6700.
D) 0.2100.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
61
A student has to take 12 more courses before he can graduate.If none of the courses are prerequisite to others, how many groups of four courses can he select for the next semester?

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
62
From among 8 students how many committees consisting of 4 students can be selected?

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
63
Assume your favorite soccer team has 3 games left to finish the season.The outcome of each game can be win, lose, or tie.How many possible outcomes exist?
A) 7
B) 27
C) 36
D) 64
A) 7
B) 27
C) 36
D) 64

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
64
If P(A) = 0.50, P(B) = 0.40 and P(A ∪ B) = 0.88, then P(B | A) =
A) 0.02.
B) 0.03.
C) 0.04.
D) 0.05.
A) 0.02.
B) 0.03.
C) 0.04.
D) 0.05.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
65
From a group of ten finalists to a contest, three individuals are to be selected for the first and second and third places.Determine the number of possible selections.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
66
Revised probabilities of events based on additional information are _____ probabilities.
A) joint
B) posterior
C) independent
D) complementary
A) joint
B) posterior
C) independent
D) complementary

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
67
If P(A) = 0.45, P(B) = 0.55, and P(A ∪ B) = 0.78, then P(A | B) =
A) 0.00
B) 0.45
C) 0.22
D) 0.40
A) 0.00
B) 0.45
C) 0.22
D) 0.40

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
68
If A and B are independent events with P(A) = 0.38 and P(B) = 0.55, then P(A | B) =
A) 0.209.
B) 0.000.
C) 0.550.
D) 0.380.
A) 0.209.
B) 0.000.
C) 0.550.
D) 0.380.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
69
If A and B are independent events with P(A) = 0.35 and P(B) = 0.20, then, P(A ∪ B) =
A) 0.07.
B) 0.62.
C) 0.55.
D) 0.48.
A) 0.07.
B) 0.62.
C) 0.55.
D) 0.48.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
70
A college plans to interview 7 students for possible offer of graduate assistantships.The college has three assistantships available.How many groups of three can the college select?

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
71
Six puppies were born in a litter, and it is determined whether each puppy is male or female.How many sample points exist in the above experiment?
A) 64
B) 32
C) 16
D) 4
A) 64
B) 32
C) 16
D) 4

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
72
If X and Y are mutually exclusive events with P(A) = 0.295, P(B) = 0.32, then P(A | B) =
A) 0.0944.
B) 0.6150.
C) 1.0000.
D) 0.0000.
A) 0.0944.
B) 0.6150.
C) 1.0000.
D) 0.0000.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
73
If A and B are independent events with P(A) = 0.4 and P(B) = 0.25, then P(A ∪ B) =
A) 0.65.
B) 0.55.
C) 0.10.
D) 0.75.
A) 0.65.
B) 0.55.
C) 0.10.
D) 0.75.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
74
If P(A) = 0.48, P(A ∪ B) = 0.82, and P(B) = 0.54, then P(A ∩ B) =
A) 0.3936.
B) 0.3400.
C) 0.2000.
D) 1.0200.
A) 0.3936.
B) 0.3400.
C) 0.2000.
D) 1.0200.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
75
Each customer entering a department store will either buy or not buy some merchandise.An experiment consists of following 3 customers and determining whether or not they purchase any merchandise.How many sample points exist in the above experiment? (Note that each customer is either a purchaser or non-purchaser.)
A) 3
B) 6
C) 8
D) 9
A) 3
B) 6
C) 8
D) 9

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
76
Some of the CDs produced by a manufacturer are defective.From the production line, 4 CDs are selected and inspected.How many sample points exist in this experiment?
A) 4
B) 8
C) 16
D) 256
A) 4
B) 8
C) 16
D) 256

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
77
If P(A) = 0.7, P(B) = 0.6, P(A ∩ B) = 0, then events A and B are
A) supplementary events.
B) mutually exclusive.
C) independent events.
D) complements of each other.
A) supplementary events.
B) mutually exclusive.
C) independent events.
D) complements of each other.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
78
From nine cards numbered 1 through 9, two cards are drawn.Consider the selection and classification of the cards as odd or even as an experiment.How many sample points are there for this experiment?
A) 2
B) 3
C) 4
D) 9
A) 2
B) 3
C) 4
D) 9

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
79
The probability of at least one head in two flips of a coin is
A) 0.25.
B) 0.33.
C) 0.50.
D) 0.75.
A) 0.25.
B) 0.33.
C) 0.50.
D) 0.75.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
80
Twelve individuals are candidates for positions of president and vice president of an organization.How many possibilities of selections exist?

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck


