Deck 11: Two-Factor Between-Subjects Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/92
Play
Full screen (f)
Deck 11: Two-Factor Between-Subjects Analysis of Variance
1
11-14 A 2 × 2 between-subjects factorial design with ten scores per cell requires participants.
A)10
B)20
C)40
D)80
A)10
B)20
C)40
D)80
C
2
11-19 A main effect mean for factor A in a factorial design is represented by. 



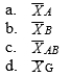




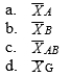
A
3
In a factorial design, a cell is another term for a(n).
A)individual subject
B)main effect
C)treatment condition
D)level of an independent variable
A)individual subject
B)main effect
C)treatment condition
D)level of an independent variable
C
4
The simplest factorial design is a design.
A)1 × 1
B)1 × 2
C)2 × 1
D)2 × 2
A)1 × 1
B)1 × 2
C)2 × 1
D)2 × 2

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
5
11-18 In a 2 × 2 factorial design, there will be a total of cell mean(s) for the analysis of variance.
A)four
B)eight
C)two
D)one
A)four
B)eight
C)two
D)one

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
6
11-20 A main effect mean in a factorial design represents the.
A)total of all scores divided by N
B)principal source of variation in an experiment
C)mean of all levels of one independent variable
D)mean of one level of an independent variable
A)total of all scores divided by N
B)principal source of variation in an experiment
C)mean of all levels of one independent variable
D)mean of one level of an independent variable

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
7
11-17 A cell mean in a factorial design is represented by. 
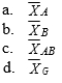

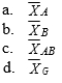

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
8
The one-factor analysis of variance is limited to analyzing research designs using.
A)one level of one independent variable
B)three or more independent variables
C)one independent variable
D)two levels of one independent variable
A)one level of one independent variable
B)three or more independent variables
C)one independent variable
D)two levels of one independent variable

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
9
Factorial designs are research designs in which independent variable(s) is/are simultaneously varied.
A)one
B)one or more
C)two or more
D)at least three
A)one
B)one or more
C)two or more
D)at least three

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
10
11-13 A 3 × 2 factorial design creates treatment conditions.
A)six
B)five
C)two
D)three
A)six
B)five
C)two
D)three

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
11
11-11 A 2 × 2 factorial design creates treatment conditions.
A)two
B)four
C)six
D)eight
A)two
B)four
C)six
D)eight

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
12
A factorial design is one in which two or more are simultaneously varied.
A)dependent variables
B)levels of one independent variable
C)independent variables
D)extraneous variables
A)dependent variables
B)levels of one independent variable
C)independent variables
D)extraneous variables

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
13
11-10 In a factorial design a treatment condition represents a.
A)placebo treatment
B)level of one independent variable
C)main effect treatment
D)combination of one level from each independent variable
A)placebo treatment
B)level of one independent variable
C)main effect treatment
D)combination of one level from each independent variable

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
14
11-16 A 3 × 3 between-subjects factorial design with ten scores per cell requires participants.
A)90
B)30
C)60
D)10
A)90
B)30
C)60
D)10

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
15
A 3 × 3 design has independent variables with levels for each.
A)two; two
B)two; three
C)three; two
D)three; three
A)two; two
B)two; three
C)three; two
D)three; three

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
16
A 2 × 3 factorial design has.
A)two independent variables, each with three levels
B)two independent variables, one with two levels and one with three levels
C)six independent variables
D)three independent variables, each with two levels
A)two independent variables, each with three levels
B)two independent variables, one with two levels and one with three levels
C)six independent variables
D)three independent variables, each with two levels

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
17
A limitation of the one-factor analysis of variance is that it can only be used to analyze research designs with.
A)one independent variable
B)two independent variables
C)two levels of one independent variable
D)three or more levels of one independent variable
A)one independent variable
B)two independent variables
C)two levels of one independent variable
D)three or more levels of one independent variable

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
18
11-12 A 3 × 3 factorial design creates treatment conditions.
A)two
B)six
C)three
D)nine
A)two
B)six
C)three
D)nine

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
19
A 2 × 2 × 2 factorial design indicates independent variables are used with each variable assuming levels.
A)three; two
B)three; three
C)two; three
D)two; two
A)three; two
B)three; three
C)two; three
D)two; two

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
20
11-15 A 3 × 2 between-subjects factorial design with ten scores per cell requires participants.
A)50
B)60
C)10
D)30
A)50
B)60
C)10
D)30

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
21
11-42 The difference 
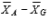 is involved in the computation of SS in a two-factor between-subjects analysis of variance.
is involved in the computation of SS in a two-factor between-subjects analysis of variance.
A)Total
B)A
C)Error
D)A × B

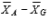 is involved in the computation of SS in a two-factor between-subjects analysis of variance.
is involved in the computation of SS in a two-factor between-subjects analysis of variance.A)Total
B)A
C)Error
D)A × B

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
22
11-32 represents the effect of factor B and sampling error in the partitioned score of a subject in a two-factor between-subjects analysis of variance. 

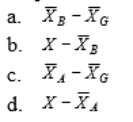


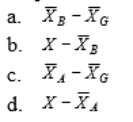

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
23
11-40 In a two-factor between-subjects analysis of variance, the interaction of two independent variables is reflected in the remaining deviation of a mean from a mean after the main effects of each independent variable have been removed.
A)main effect; grand
B)main effect; treatment group
C)cell; grand
D)cell; main effect
A)main effect; grand
B)main effect; treatment group
C)cell; grand
D)cell; main effect

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
24
11-41 The difference 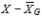 is involved in the computation of SS in a two-factor between-subjects analysis of variance.
is involved in the computation of SS in a two-factor between-subjects analysis of variance.
A)Total
B)A
C)Error
D)A × B
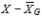 is involved in the computation of SS in a two-factor between-subjects analysis of variance.
is involved in the computation of SS in a two-factor between-subjects analysis of variance.A)Total
B)A
C)Error
D)A × B

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
25
11-28 In a two-factor between-subjects analysis of variance, F statistic(s) is/are calculated.
A)one
B)two
C)three
D)four
A)one
B)two
C)three
D)four

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
26
11-27 A two-factor between-subjects analysis of variance partitions the total variation into between-groups and within-groups sources.
A)three; one
B)three; no
C)four; no
D)one; three
A)three; one
B)three; no
C)four; no
D)one; three

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
27
11-34 represents within-cells error variation in the partitioned score of a subject in a two-factor between-subjects analysis of variance. 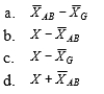
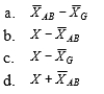

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
28
11-26 An interaction is analyzed by comparing differences.
A)between main effect means
B)between a main effect mean and the grand mean
C)among cell means
D)between cell means and the grand mean
A)between main effect means
B)between a main effect mean and the grand mean
C)among cell means
D)between cell means and the grand mean

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
29
11-30 represents the total variation in the partitioned score of a subject in a two-factor between-subjects analysis of variance. 
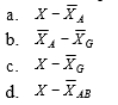

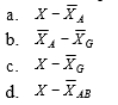

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
30
11-25 An interaction in a factorial design is defined as.
A)a situation in which the effect of one independent variable depends upon the level of the other independent variable
B)the difference between main effect means for factors A and B
C)the sum of main effect means for factors A and B
D)the effect of one independent variable averaged across levels of the other independent variable
A)a situation in which the effect of one independent variable depends upon the level of the other independent variable
B)the difference between main effect means for factors A and B
C)the sum of main effect means for factors A and B
D)the effect of one independent variable averaged across levels of the other independent variable

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
31
11-35 The difference . 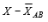 in a two-factor between-subjects analysis of variance reflects the
in a two-factor between-subjects analysis of variance reflects the
A)main effect of factor A alone
B)main effect of factor A plus sampling error
C)total variation in the score
D)within-cells error variation
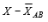 in a two-factor between-subjects analysis of variance reflects the
in a two-factor between-subjects analysis of variance reflects theA)main effect of factor A alone
B)main effect of factor A plus sampling error
C)total variation in the score
D)within-cells error variation

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
32
11-37 The difference  .
. 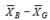 in a two-factor between-subjects analysis of variance reflects the
in a two-factor between-subjects analysis of variance reflects the
A)main effect of factor A plus sampling error
B)main effect of factor B plus sampling error
C)effect of the interaction of factors A and B plus sampling error
D)within-cells error variation
 .
. 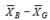 in a two-factor between-subjects analysis of variance reflects the
in a two-factor between-subjects analysis of variance reflects theA)main effect of factor A plus sampling error
B)main effect of factor B plus sampling error
C)effect of the interaction of factors A and B plus sampling error
D)within-cells error variation

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
33
11-38 The term 



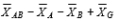 in a two-factor between-subjects analysis of variance reflects the.
in a two-factor between-subjects analysis of variance reflects the.
A)main effect of factor A plus sampling error
B)main effect of factor B plus sampling error
C)effect of the interaction of factors A and B plus sampling error
D)within-cells error variation




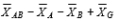 in a two-factor between-subjects analysis of variance reflects the.
in a two-factor between-subjects analysis of variance reflects the.A)main effect of factor A plus sampling error
B)main effect of factor B plus sampling error
C)effect of the interaction of factors A and B plus sampling error
D)within-cells error variation

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
34
11-24 A main effect of an independent variable in a factorial design is defined as the.
A)effect of one independent variable subtracted from the grand mean
B)difference between the main effect means for factor A and those for factor B
C)sum of main effect means for factors A and B
D)effect of one independent variable averaged across levels of the other independent variable
A)effect of one independent variable subtracted from the grand mean
B)difference between the main effect means for factor A and those for factor B
C)sum of main effect means for factors A and B
D)effect of one independent variable averaged across levels of the other independent variable

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
35
11-31 represents the effect of factor A and sampling error in the partitioned score of a subject in a two-factor between-subjects analysis of variance. 
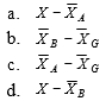

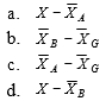

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
36
11-36 The difference . 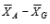 in a two-factor between-subjects analysis of variance reflects the
in a two-factor between-subjects analysis of variance reflects the
A)main effect of factor A plus sampling error
B)main effect of factor B plus sampling error
C)effect of the interaction of factors A and B plus sampling error
D)within-cells error variation
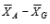 in a two-factor between-subjects analysis of variance reflects the
in a two-factor between-subjects analysis of variance reflects theA)main effect of factor A plus sampling error
B)main effect of factor B plus sampling error
C)effect of the interaction of factors A and B plus sampling error
D)within-cells error variation

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
37
11-33 represents the effect of the interaction of factors A and B and sampling error in the partitioned score of a subject in a two-factor between-subjects analysis of variance. 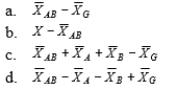
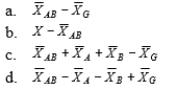

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
38
11-43 The difference 

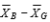 is involved in the computation of SS in a two-factor between-subjects analysis of variance.
is involved in the computation of SS in a two-factor between-subjects analysis of variance.
A)Total
B)A
C)B
D)A × B


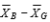 is involved in the computation of SS in a two-factor between-subjects analysis of variance.
is involved in the computation of SS in a two-factor between-subjects analysis of variance.A)Total
B)A
C)B
D)A × B

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
39
11-21 The effect of one independent variable in a factorial design is called a(n) effect.
A)source
B)level
C)main
D)independent
A)source
B)level
C)main
D)independent

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
40
11-39 The difference . 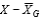 in a two-factor between-subjects analysis of variance reflects the
in a two-factor between-subjects analysis of variance reflects the
A)main effect of factor A plus sampling error
B)main effect of factor B plus sampling error
C)total variation in the score
D)within-cells error variation
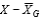 in a two-factor between-subjects analysis of variance reflects the
in a two-factor between-subjects analysis of variance reflects theA)main effect of factor A plus sampling error
B)main effect of factor B plus sampling error
C)total variation in the score
D)within-cells error variation

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
41
11-63 The F statistic for factor B in a two-factor between-subjects analysis of variance is formed by dividing MSB by.
A)MSError
B)MSA
C)MSA × B
D)SSTotal
A)MSError
B)MSA
C)MSA × B
D)SSTotal

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
42
11-44 The term 
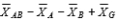 is involved in the computation of SS in a two-factor between-subjects analysis of variance.
is involved in the computation of SS in a two-factor between-subjects analysis of variance.
A)A × B
B)B
C)Total
D)A

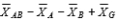 is involved in the computation of SS in a two-factor between-subjects analysis of variance.
is involved in the computation of SS in a two-factor between-subjects analysis of variance.A)A × B
B)B
C)Total
D)A

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
43
11-45 The difference -is involved in the computation of SS in a two-factor 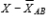 between-subjects analysis of variance.
between-subjects analysis of variance.
A)Total
B)A
C)B
D)Error
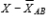 between-subjects analysis of variance.
between-subjects analysis of variance.A)Total
B)A
C)B
D)Error

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
44
11-61 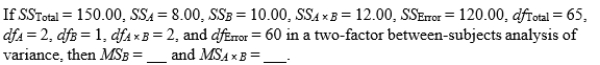
A)6.00; 10.00
B)10.00; 80.00
C)5.00; 12.00
D)10.00; 6.00
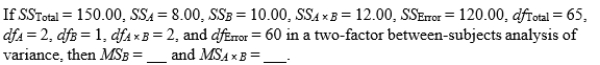
A)6.00; 10.00
B)10.00; 80.00
C)5.00; 12.00
D)10.00; 6.00

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
45
11-49 The degrees of freedom for factor B in a two-factor between-subjects analysis of variance are given by.
A)N - 1
B)(a - 1)(b - 1)
C)ab - 1
D)b - 1
A)N - 1
B)(a - 1)(b - 1)
C)ab - 1
D)b - 1

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
46
11-52 Suppose a 2 × 2 between-subjects design had 11 participants randomly assigned to each cell. The df for SSTotal are equal to and the df for SSError are equal to for the analysis of variance of this design.
A)43; 40
B)40; 43
C)44; 43
D)45; 44
A)43; 40
B)40; 43
C)44; 43
D)45; 44

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
47
11-55 Suppose a 3 × 2 between-subjects design had 10 participants randomly assigned to each cell. The df for SSA × B are for the analysis of variance of this design.
A)1
B)2
C)3
D)5
A)1
B)2
C)3
D)5

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
48
11-48 The degrees of freedom for factor A in a two-factor between-subjects analysis of variance are given by.
A)N - 1
B)(a - 1)(b - 1)
C)a - 1
D)a - 2
A)N - 1
B)(a - 1)(b - 1)
C)a - 1
D)a - 2

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
49
11-50 The degrees of freedom for the interaction of factors A and B in a two-factor between-subjects analysis of variance are given by.
A)N - 1
B)(a - 1)(b - 1)
C)ab - 1
D)(a + 1)(b + 1)
A)N - 1
B)(a - 1)(b - 1)
C)ab - 1
D)(a + 1)(b + 1)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
50
11-58 The mean square for the interaction of factors A and B in a two-factor between subjects analysis of variance is defined as SSA × B divided by.
A)ab
B)dfA
C)(a - 1)(b - 1)
D)ab - 1
A)ab
B)dfA
C)(a - 1)(b - 1)
D)ab - 1

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
51
11-53 Suppose a 3 × 2 between-subjects design had 10 participants randomly assigned to each cell. The df for SSTotal are equal to and the df for SSA are equal to for the analysis of variance of this design.
A)59; 1
B)59; 2
C)54; 2
D)60; 2
A)59; 1
B)59; 2
C)54; 2
D)60; 2

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
52
11-54 Suppose a 3 × 2 between-subjects design had 10 participants randomly assigned to each cell. The df for SSB are equal to and the df for SSError are equal to for the analysis of variance of this design.
A)1; 59
B)2; 54
C)2; 59
D)1; 54
A)1; 59
B)2; 54
C)2; 59
D)1; 54

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
53
11-46 If SSTotal = 500.00, SSA = 150.00, SSB = 50.00, and SSError = 100.00 in a two-factor between-subjects analysis of variance, then SSA × B =.
A)800.00
B)300.00
C)150.00 d 200.00
A)800.00
B)300.00
C)150.00 d 200.00

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
54
11-51 The degrees of freedom for the error in a two-factor between-subjects analysis of variance are given by.
A)N - 1
B)(a - 1)(b - 1)
C)ab(nAB - 1)
D)ab(nAB + 1)
A)N - 1
B)(a - 1)(b - 1)
C)ab(nAB - 1)
D)ab(nAB + 1)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
55
11-60 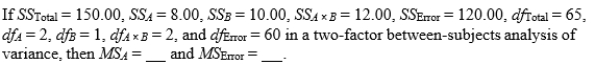
A)4.00; 6.00
B)4.00; 2.00
C)16.00; 7200.00
D)8.00; 30.00
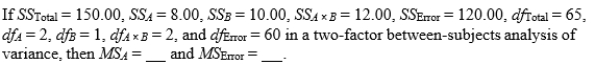
A)4.00; 6.00
B)4.00; 2.00
C)16.00; 7200.00
D)8.00; 30.00

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
56
11-57 The mean square for factor B in a two-factor between-subjects analysis of variance is defined as SSB divided by.
A)b
B)dfTotal
C)SSTotal
D)b - 1
A)b
B)dfTotal
C)SSTotal
D)b - 1

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
57
11-47 The total degrees of freedom in a two-factor between-subjects analysis of variance is defined as the number of minus one.
A)independent variables
B)treatment conditions
C)scores
D)subjects in each treatment condition
A)independent variables
B)treatment conditions
C)scores
D)subjects in each treatment condition

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
58
11-62 The F statistic for factor A in a two-factor between-subjects analysis of variance is formed by dividing MSA by.
A)MSB
B)MSA × B
C)MSError
D)SSTotal
A)MSB
B)MSA × B
C)MSError
D)SSTotal

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
59
11-56 The mean square for factor A in a two-factor between-subjects analysis of variance is defined as SSA divided by.
A)a
B)a - 1
C)dfTotal
D)SSTotal
A)a
B)a - 1
C)dfTotal
D)SSTotal

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
60
11-59 The mean square for the error term in a two-factor between-subjects analysis of variance is defined as the SSError divided by.
A)ab
B)(a - 1)(b - 1)
C)N - 1
D)ab(nAB - 1)
A)ab
B)(a - 1)(b - 1)
C)N - 1
D)ab(nAB - 1)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
61
11-89 Which of the following is not true if Fobs for the interaction in a two-factor between-subjects analysis of variance is statistically significant?
A)The simple effects of factor A are not equal to the main effect of factor A.
B)The simple effects of factor B are not equal to the main effect of factor B.
C)The simple effect of factor A at B1 is not equal to the simple effect of factor A at B2.
D)The simple effects of factors A and B do not differ from their main effects.
A)The simple effects of factor A are not equal to the main effect of factor A.
B)The simple effects of factor B are not equal to the main effect of factor B.
C)The simple effect of factor A at B1 is not equal to the simple effect of factor A at B2.
D)The simple effects of factors A and B do not differ from their main effects.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
62
11-74 The null hypothesis for the interaction of factors A and B in a 3 × 4 between-subjects analysis of variance is H0:. 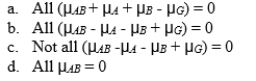
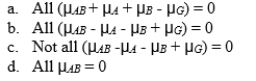

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
63
11-69 If factor A produces a main effect in a two-factor between-subjects analysis of variance, then will increase in value relative to MSError.
A)MSA
B)MSB
C)MSA × B
D)both MSA and MSA × B
A)MSA
B)MSB
C)MSA × B
D)both MSA and MSA × B

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
64
11-71 If the independent variables interact in a two-factor between-subjects analysis of variance, then will increase in value relative to MSError.
A)MSA
B)MSB
C)MSA × B
D)all the above
A)MSA
B)MSB
C)MSA × B
D)all the above

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
65
11-70 If factor B produces a main effect in a two-factor between-subjects analysis of variance, then will increase in value relative to MSError.
A)MSA
B)MSA × B
C)MSB
D)both MSB and MSA × B
A)MSA
B)MSA × B
C)MSB
D)both MSB and MSA × B

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
66
11-78 H0 is rejected if Fobs in a two-factor between-subjects analysis of variance is its corresponding critical value.
A)smaller than
B)equal to or larger than
C)either smaller than or larger than
D)none of the above
A)smaller than
B)equal to or larger than
C)either smaller than or larger than
D)none of the above

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
67
11-81 The following values of Fobs occurred in a two-factor between-subjects analysis of variance: F(1, 28) for factor A = 3.47, F(1, 28) for factor B = 4.29, and F(1, 28) for the interaction of factors A and B = 4.10. Fcrit(1, 28) = 4.20 for alpha = .05. In this experiment you would H0 for factor A, H0 for factor B, and H0 for the interaction of factors A and B.
A)reject; reject; reject
B)fail to reject; fail to reject; fail to reject
C)fail to reject; reject; fail to reject
D)reject; fail to reject; reject
A)reject; reject; reject
B)fail to reject; fail to reject; fail to reject
C)fail to reject; reject; fail to reject
D)reject; fail to reject; reject

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
68
11-64 The F statistic for interaction in a two-factor between-subjects analysis of variance is formed by dividing MSError into.
A)MSA
B)MSA × B
C)MSB
D)SSTotal
A)MSA
B)MSA × B
C)MSB
D)SSTotal

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
69
11-67 The MSB term in a two-factor between-subjects analysis of variance responds to the systematic variation due to factor B and.
A)sampling error
B)factor A
C)sample size of each treatment group
D)the interaction of factors A and B
A)sampling error
B)factor A
C)sample size of each treatment group
D)the interaction of factors A and B

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
70
11-65 If MSA = 4.00, MSB = 10.00, MSA × B = 6.00, and MSError = 2.00 in a two-factor between-subjects analysis of variance, then Fobs for factor A = , Fobs for factor B = ,
And Fobs for the interaction of factors A and B =.
A)3.00; 2.00; 5.00
B)2.00; 5.00; 3.00
C)2.00; 3.00; 5.00
D)5.00; 3.00; 2.00
And Fobs for the interaction of factors A and B =.
A)3.00; 2.00; 5.00
B)2.00; 5.00; 3.00
C)2.00; 3.00; 5.00
D)5.00; 3.00; 2.00

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
71
11-84 A effect of an independent variable in a factorial design is the effect of that independent variable at of the other independent variable.
A)simple; both levels
B)simple; only one level
C)factorial; all
D)main; only one level
A)simple; both levels
B)simple; only one level
C)factorial; all
D)main; only one level

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
72
11-79 H0 is not rejected if Fobs in a two-factor between-subjects analysis of variance is its corresponding critical value.
A)less than
B)equal to
C)larger than
D)none of the above
A)less than
B)equal to
C)larger than
D)none of the above

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
73
11-77 The alternative hypothesis for the interaction of factors A and B in a 3 × 4 between-subjects analysis of variance is H1:. 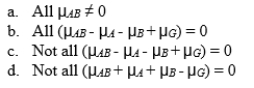
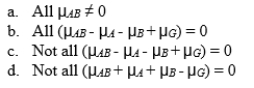

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
74
11-88 If an interaction of the independent variables occurs in a two-factor between-subjects analysis of variance, then the simple effects of a factor will be to each other and to the main effect for that factor.
A)unequal; unequal
B)unequal; equal
C)equal; equal
D)equal; unequal
A)unequal; unequal
B)unequal; equal
C)equal; equal
D)equal; unequal

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
75
11-83 A two-factor between-subjects analysis of variance is based upon the assumption that the in the populations sampled.
A)scores are symmetrical and bimodal
B)means are equal
C)means are normally distributed
D)variances of scores are equal
A)scores are symmetrical and bimodal
B)means are equal
C)means are normally distributed
D)variances of scores are equal

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
76
11-85 A simple effect refers to the in a factorial design.
A)difference between the main effect means for an independent variable
B)difference between a cell mean and a grand mean
C)difference between a cell mean and a main effect mean
D)effect of one independent variable at only one level of another independent variable
A)difference between the main effect means for an independent variable
B)difference between a cell mean and a grand mean
C)difference between a cell mean and a main effect mean
D)effect of one independent variable at only one level of another independent variable

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
77
11-66 The MSA term in a two-factor between-subjects analysis of variance responds to the systematic variation due to factor A and.
A)the grand mean
B)sampling error
C)sample size of each treatment group
D)degrees of freedom for factor A
A)the grand mean
B)sampling error
C)sample size of each treatment group
D)degrees of freedom for factor A

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
78
11-68 The MSA × B term in a two-factor between-subjects analysis of variance responds to the systematic variation due to the interaction of factors A and B and.
A)the grand mean
B)sample size of each treatment group
C)the main effects of factors A and B
D)sampling error
A)the grand mean
B)sample size of each treatment group
C)the main effects of factors A and B
D)sampling error

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
79
11-80 The following values of Fobs occurred in a two-factor between-subjects analysis of variance: F(1, 40) for factor A = 4.76, F(1, 40) for factor B = 3.81, and F(1, 40) for the interaction of factors A and B = 5.03. Fcrit(1, 40) = 4.08 for alpha = .05. In this experiment you would H0 for factor A, H0 for factor B, and H0 for the interaction of factors A and B.
A)reject; reject; reject
B)fail to reject; fail to reject; fail to reject
C)fail to reject; reject; fail to reject
D)reject; fail to reject; reject
A)reject; reject; reject
B)fail to reject; fail to reject; fail to reject
C)fail to reject; reject; fail to reject
D)reject; fail to reject; reject

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
80
11-82 A two-factor between-subjects analysis of variance is based upon the assumption that the in the populations sampled are.
A)scores; symmetrical and unimodal
B)scores; normally distributed
C)means; equal
D)means; normally distributed
A)scores; symmetrical and unimodal
B)scores; normally distributed
C)means; equal
D)means; normally distributed

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck


