Deck 21: Nonparametric Techniques
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/136
Play
Full screen (f)
Deck 21: Nonparametric Techniques
1
Which of the following distributions approximates the Kruskal-Wallis test statistic H when the problem objective is to compare k distributions and the sample sizes are greater than or equal to 5? 

B
2
The significance level for a Wilcoxon signed rank sum test is 0.05. The alternative hypothesis is stated as: The location of population 1 is to the left of the location of population 2. The appropriate critical value for a sample of size 20 (that is, the number of nonzero differences) is: 

C
3
Which of the following is the alternative hypothesis tested in applications of the Kruskal-Wallis test? 

C
4
In a Wilcoxon signed rank sum test for matched pairs with n = 35, the rank sums of the positive and negative differences are 380 and 225, respectively. The value of the standardised test statistic z is: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
5
A matched pairs experiment yielded the following paired differences:  The value of the standardised sign test statistic z is:
The value of the standardised sign test statistic z is: 
 The value of the standardised sign test statistic z is:
The value of the standardised sign test statistic z is: 

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
6
In a sign test, the following information is given: number of zero differences = 3, number of positive differences = 20, and number of negative differences = 5. The value of the standardised test statistic z is: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
7
Consider the following data set:  The rank assigned to the four observations of value 22 is:
The rank assigned to the four observations of value 22 is: 
 The rank assigned to the four observations of value 22 is:
The rank assigned to the four observations of value 22 is: 

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
8
Which of the following is the non-parametric equivalent to the parametric t-test of 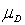 for matched pairs?
for matched pairs? 
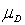 for matched pairs?
for matched pairs? 

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
9
In a Kruskal-Wallis test there are five samples and the value of the test statistic is calculated as H = 11.15. The most accurate statement that can be made about the p-value is that: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
10
Consider the following data set:  The rank assigned to the three observations of value 1.3 is:
The rank assigned to the three observations of value 1.3 is: 
 The rank assigned to the three observations of value 1.3 is:
The rank assigned to the three observations of value 1.3 is: 

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
11
In a Wilcoxon signed rank sum test, the test statistic is calculated as T = 75. If there are n = 15 observations for which 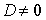 , and a two-tail test is performed at the 5% significance level, then:
, and a two-tail test is performed at the 5% significance level, then: 
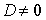 , and a two-tail test is performed at the 5% significance level, then:
, and a two-tail test is performed at the 5% significance level, then: 

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
12
Consider the following two samples:  The value of the test statistic for a right-tailed Wilcoxon rank sum test is:
The value of the test statistic for a right-tailed Wilcoxon rank sum test is: 
 The value of the test statistic for a right-tailed Wilcoxon rank sum test is:
The value of the test statistic for a right-tailed Wilcoxon rank sum test is: 

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
13
The significance level for a Wilcoxon signed rank sum test is 0.05. The alternative hypothesis is stated as: the location of population 1 is to the right of the location of population 2. The appropriate critical value for a sample of size 20 (that is, the number of nonzero differences is 20) is: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
14
The Kruskal-Wallis test statistic can be approximated by a Chi-squared distribution with k - 1 degrees of freedom (where k is the number of populations) whenever the sample sizes are all greater than or equal to: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
15
The significance level for a Wilcoxon signed rank sum test is 0.05. The alternative hypothesis is stated as: The location of population 1 is left to the location of population 2. The appropriate critical values for a sample of size 20 (that is the number of nonzero differences is 20) are: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following is the correct sample size requirement for the Wilcoxon signed rank sum test statistic to be approximately normally distributed? 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
17
A Wilcoxon rank sum test for comparing two populations involves two independent samples of sizes 5 and 7. The alternative hypothesis is stated as: The location of population 1 is different from the location of population 2. The appropriate critical values at the 5% significance level are: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
18
In a normal approximation to the Wilcoxon signed rank sum test, the test statistic is calculated as z = 1.59. For a two-tail test, the p-value is: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
19
In a Wilcoxon signed rank sum test, the test statistic is calculated as T = 45. The alternative hypothesis is stated as: The location of population 1 is different from the location of population 2. If there are n = 15 observations for which 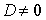 , and the 5% significance level is used, then:
, and the 5% significance level is used, then: 
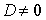 , and the 5% significance level is used, then:
, and the 5% significance level is used, then: 

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
20
Consider the following two samples:  The value of the test statistic for a left-tailed Wilcoxon rank sum test is:
The value of the test statistic for a left-tailed Wilcoxon rank sum test is: 
 The value of the test statistic for a left-tailed Wilcoxon rank sum test is:
The value of the test statistic for a left-tailed Wilcoxon rank sum test is: 

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
21
Which of the following tests would be an example of a non-parametric method? 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
22
Compared to parametric tests, non-parametric tests use the information contained in the data: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
23
A non-parametric method to compare two populations, when the samples are independent but the assumptions behind the independent samples t-test are violated, is the: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
24
Which of the following best describes the hypotheses in the Kruskal-Wallis test and Friedman test? 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
25
A Wilcoxon rank sum test for comparing two populations involves two independent samples of sizes 15 and 20. The unstandardised test statistic (that is the rank sum) is T = 210. The value of the standardised test statistic z is: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
26
In a Kruskal-Wallis test for comparing five populations, the test statistic is calculated as H = 10.20. If the test is conducted at the 1% significance level, then: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
27
Which of the following are statistical methods that require few assumptions, if any, about the distribution of the population? 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
28
A non-parametric method to compare two or more populations, when the samples are matched pairs and the data are either ordinal or interval but not normal, is the: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
29
The Wilcoxon rank sum test (like most of the non-parametric tests presented in your textbook) actually tests to determine whether the population distributions have identical:

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
30
A non-parametric method to compare two populations, when the samples are matched pairs and the data are ordinal, is the: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
31
The first step in a Wilcoxon rank sum test is to combine the data values in the two samples and assign a rank of 1 to the: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
32
The non-parametric counterpart of the randomised block model of the analysis of variance is the: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
33
In a Friedman test for comparing four populations, provided that there are eight blocks, the test statistic is calculated as F = 10.98. If the test is conducted at the 5% significance level, the conclusion and p-value will be: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
34
A non-parametric method to compare two or more populations, when the samples are independent and the data are either ordinal or interval but not normal, is the: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
35
Which of the following best describes when a non-parametric test for comparing two or more populations should be used instead of its parametric counterpart? 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
36
The non-parametric tests discussed in your textbook (Wilcoxon rank sum test, sign test, Wilcoxon signed rank sum test, Kruskal-Wallis test and Friedman test) all require that the probability distributions be: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
37
A non-parametric method to compare two populations, when the samples consist of matched pairs of observations and the data are either ordinal or interval, and where the normality requirement necessary to perform the parametric test is not satisfied, is the: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
38
The appropriate measure of central location of ordinal data is the: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
39
The non-parametric counterpart of the parametric one-way analysis of variance F-test is the: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
40
Which of the following statements is correct regarding the Kruskal-Wallis test? 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
41
Which of the following best describes when to apply the Friedman test to determine whether the locations of two or more populations are the same? 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
42
In a normal approximation to the sign test, the standardised test statistic is calculated as z = -1.58. To test the alternative hypothesis that the location of population 1 is to left of the location of population 2, the p-value is: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
43
The Friedman test is the non-parametric counterpart of the randomised block experimental design of the analysis of variance.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
44
Which of the following will never be a required condition of a non-parametric test? 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
45
In a normal approximation to the Wilcoxon rank sum test, the standardised test statistic is calculated as z = 1.80. For a two- tail test, the p-value is: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
46
In a Wilcoxon rank sum test, the two sample sizes are 6 and 6, and the value of the Wilcoxon test statistic is T = 20. If the test is two-tailed and the level of significance is , then:

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
47
The F-test of the randomised block design of the analysis of variance requires that the random variable of interest must be normally distributed and the population variances must be equal. When the random variable is not normally distributed, we can use: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
48
Which of the following best describes when to apply the Wilcoxon rank sum test to determine whether the location of population 1 is different from the location of population 2? 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
49
The Kruskal-Wallis test requires independent sample.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
50
In the sign test applications, the normal approximation to the binomial distribution may be used whenever the number of nonzero differences is greater than or equal to: 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
51
The Wilcoxon rank sum test for independent samples actually tests whether the population distributions are identical.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
52
The critical value is taken from the t-distribution whenever the test is a Kruskal-Wallis test.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
53
The Friedman test statistic is approximately chi-squared distributed with (k - 1) degrees of freedom, provided that either the number of blocks b or the number of treatments k is greater than or equal to 5.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
54
A non-parametric test is one that makes no assumptions about the specific shape of the population from which a sample is drawn.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
55
The Wilcoxon signed rank sum test is the nonparametric counterpart of the t-test of µD.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
56
A one-sample t-test is the parametric counterpart of the Friedman test for randomised block experimental design.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
57
The z-test approximation to the Wilcoxon rank sum test for two independent samples requires that at least one of the two sample sizes exceed 10.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
58
Which of the following best describes when the Wilcoxon rank sum test statistic T is approximately normally distributed? 


Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
59
The sign test and the Wilcoxon signed rank sum test require matched pairs.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
60
A two-independent-sample t-test corresponds to a Wilcoxon signed rank sum test for paired samples.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
61
The Friedman test is employed to compare two or more populations when the data are generated from a matched pairs experiment, and are either ordinal or interval but not normally distributed.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
62
Use the 5% significance level to test the hypotheses. The two population locations are the same The location of population A is to the left of the location of population B,
given that the data below are drawn from a matched pairs experiment.
given that the data below are drawn from a matched pairs experiment.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
63
We can use the Friedman test to determine whether a difference exists between two populations. However, if we want to determine whether one population location is larger than another, we must use the sign test.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
64
We can use the Friedman test to determine whether two populations differ. The conclusion will be the same as that produced by the sign test.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
65
The sign test is employed to compare two populations when the experimental design is matched pairs, and the data are ordinal but not normally distributed.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
66
In a normal approximation to the sign test, the standardised test statistic is calculated as z = 2.07. If the alternative hypothesis states that the location of population 1 is to the right of the location of population 2, then the p-value of the test is 0.0192.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
67
The Wilcoxon rank sum test is used to compare two populations when the samples are independent and the data are either ordinal or interval but not normally distributed.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
68
The Kruskal-Wallis test can be used to test for a difference between two populations. It will produce the same outcome as the two-tailed Wilcoxon rank sum test.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
69
A Wilcoxon rank sum test for comparing two independent samples involves two samples of sizes 5 and 8. The alternative hypothesis is that the location of population 1 is different from the location of population 2. Using the 0.10 significance level, the appropriate critical values are 21 and 49.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
70
The Kruskal-Wallis test is applied to compare two or more populations when the samples are independent and the data are ordinal or numerical and non-normal.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
71
Given the following statistics from a matched pairs experiment, perform the Wilcoxon signed rank sum test to determine whether we can infer at the 10% significance level that the two population locations differ. 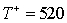
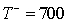 , n = 50
, n = 50
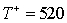
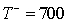 , n = 50
, n = 50
Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
72
The Kruskal-Wallis test can be used to determine whether a difference exists between two populations. However, to determine whether one population location is larger than another, we must apply the Wilcoxon rank sum test.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
73
The Wilcoxon signed rank sum test is applied to compare two populations when the samples are matched pairs and the data are interval but not normally distributed.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
74
The Kruskal-Wallis test uses the Chi-squared distribution.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
75
In a normal approximation to the Wilcoxon rank sum test, the standardised test statistic is calculated as z = 1.96. For a two-tailed test, the p-value is 0.025.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
76
A Wilcoxon rank sum test for comparing two independent samples involves two samples of sizes 6 and 9. The alternative hypothesis is that the location of population 1 is to the left of the location of population 2. Using the 0.05 significance level, the appropriate critical values are 31 and 65.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
77
A Wilcoxon rank sum test for comparing two populations involves two independent samples of sizes 15 and 20. The value of the unstandardised test statistic is T = 225. The value of the standardised test statistic is z = -1.50.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
78
One of the required conditions of the sign test is that the number of nonzero differences n must be smaller than or equal to 10.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
79
In a Wilcoxon rank sum test for independent samples, the two sample sizes are 4 and 6, and the value of the Wilcoxon test statistic is T = 25. If the test is two-tailed and the level of significance is 0.05, then the null hypothesis will be rejected.

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck
80
Radio advertising is big business, second only to television advertising. The objective for radio advertisements is to get listeners to remember as much as possible about the product/service being advertised. The advertising executive of a large company must decide between two pitched radio advertisements for their company. In order to ascertain the general public's perception, 12 randomly chosen people are selected to listen to both potential advertisements and are then asked a series of 5 questions regarding the radio advertisement's content. The number of correct responses are recorded and listed below. Assume that responses are non-normal. 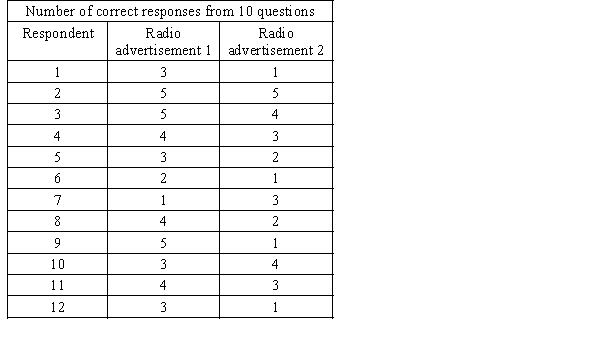 a. Which test is appropriate for this situation?
a. Which test is appropriate for this situation?
b. Do these data provide enough evidence at the 5% significance level to conclude that the two radio advertisements differ?
 a. Which test is appropriate for this situation?
a. Which test is appropriate for this situation?b. Do these data provide enough evidence at the 5% significance level to conclude that the two radio advertisements differ?

Unlock Deck
Unlock for access to all 136 flashcards in this deck.
Unlock Deck
k this deck


