Deck 9: Project Scheduling: Pertcpm
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/59
Play
Full screen (f)
Deck 9: Project Scheduling: Pertcpm
1
Critical activities are those that can be delayed without delaying the entire project.
False
2
It is possible to have more than one critical path at a time.
True
3
The length of time an activity can be delayed without affecting the project completion time is the slack.
True
4
The difference between an activity's earliest finish time and latest finish time equals the difference between its earliest start time and latest start time.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
5
PERT and CPM are applicable only when there is no dependence among activities.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
6
When activity times are uncertain, total project time is normally distributed with mean equal to the sum of the means of all of the critical activities.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
7
A path through a project network must reach every node.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
8
The earliest finish time for the final activity is the project duration.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
9
The variance in the project completion time is the sum of the variances of all activities in the project.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
10
Constraints in the LP models for crashing decisions are required to compare the activity's earliest finish time with the earliest finish time of each predecessor.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
11
Crashing refers to an unanticipated delay in a critical path activity that causes the total time to exceed its limit.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
12
All activities on a critical path have zero slack time.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
13
A critical activity can be part of a noncritical path.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
14
The linear programming model for crashing presented in the textbook assumes that any portion of the activity crash time can be achieved for a corresponding portion of the activity crashing cost.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
15
The earliest start time for an activity is equal to the smallest of the earliest finish times for all its immediate predecessors.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
16
When activity times are uncertain, an activity's most likely time is the same as its expected time.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
17
The project manager should monitor the progress of any activity with a large time variance even if the expected time does not identify the activity as a critical activity.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
18
Precedence relationships among activities is critical in CPM analysis but not in PERT.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
19
Activities require time to complete while events do not.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
20
The latest finish time for an activity is the largest of the latest start times for all activities that immediately follow the activity.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
21
A critical activity is
A) an activity that consumes no time but shows precedence between events.
B) a milestone accomplishment within the project.
C) an activity with zero slack.
D) the beginning of an event.
A) an activity that consumes no time but shows precedence between events.
B) a milestone accomplishment within the project.
C) an activity with zero slack.
D) the beginning of an event.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
22
For an activity with more than one immediate successor activity, its latest-finish time is equal to the
A) largest latest-finish time among its immediate successors.
B) smallest latest-finish time among its immediate successors.
C) largest latest-start time among its immediate successors.
D) smallest latest-start time among its immediate successors.
A) largest latest-finish time among its immediate successors.
B) smallest latest-finish time among its immediate successors.
C) largest latest-start time among its immediate successors.
D) smallest latest-start time among its immediate successors.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
23
Activities following a node
A) can begin as soon as any activity preceding the node has been completed.
B) have an earliest start time equal to the largest of the earliest finish times for all activities entering the node.
C) have a latest start time equal to the largest of the earliest finish times for all activities entering the node.
D) None of the alternatives is correct.
A) can begin as soon as any activity preceding the node has been completed.
B) have an earliest start time equal to the largest of the earliest finish times for all activities entering the node.
C) have a latest start time equal to the largest of the earliest finish times for all activities entering the node.
D) None of the alternatives is correct.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
24
Which of the following is a general rule for crashing activities?
A) Crash only non-critical activities.
B) Crash activities with zero slack.
C) Crash activities with the greatest number of predecessors.
D) Crash the path with the fewest activities.
A) Crash only non-critical activities.
B) Crash activities with zero slack.
C) Crash activities with the greatest number of predecessors.
D) Crash the path with the fewest activities.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
25
Activities K, M and S immediately follow activity H, and their latest start times are 14, 18, and 11. The latest finish time for activity H
A) is 11.
B) is 14.
C) is 18.
D) cannot be determined.
A) is 11.
B) is 14.
C) is 18.
D) cannot be determined.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
26
Which is not a significant challenge of project scheduling?
A) deadlines exist.
B) activities are independent.
C) many employees could be required.
D) delays are costly.
A) deadlines exist.
B) activities are independent.
C) many employees could be required.
D) delays are costly.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
27
The earliest start time rule
A) compares the starting times of all activities for successors of an activity.
B) compares the finish times for all immediate predecessors of an activity.
C) determines when the project can begin.
D) determines when the project must begin.
A) compares the starting times of all activities for successors of an activity.
B) compares the finish times for all immediate predecessors of an activity.
C) determines when the project can begin.
D) determines when the project must begin.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
28
Activities G, P, and R are the immediate predecessors for activity W. If the earliest finish times for the three are 12, 15, and 10, then the earliest start time for W
A) is 10.
B) is 12.
C) is 15.
D) cannot be determined.
A) is 10.
B) is 12.
C) is 15.
D) cannot be determined.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
29
Arcs in a project network indicate
A) completion times.
B) precedence relationships.
C) activities.
D) the critical path.
A) completion times.
B) precedence relationships.
C) activities.
D) the critical path.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
30
Activities with zero slack
A) can be delayed.
B) must be completed first.
C) lie on a critical path.
D) have no predecessors.
A) can be delayed.
B) must be completed first.
C) lie on a critical path.
D) have no predecessors.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
31
When activity times are uncertain,
A) assume they are normally distributed.
B) calculate the expected time, using (a + 4m + b)/6.
C) use the most likely time.
D) calculate the expected time, using (a + m + b)/3.
A) assume they are normally distributed.
B) calculate the expected time, using (a + 4m + b)/6.
C) use the most likely time.
D) calculate the expected time, using (a + m + b)/3.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
32
In deciding which activities to crash, one must
A) crash all critical activities.
B) crash largest-duration activities.
C) crash lowest-cost activities.
D) crash activities on the critical path(s) only.
A) crash all critical activities.
B) crash largest-duration activities.
C) crash lowest-cost activities.
D) crash activities on the critical path(s) only.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
33
The critical path
A) is any path that goes from the starting node to the completion node.
B) is a combination of all paths.
C) is the shortest path.
D) is the longest path.
A) is any path that goes from the starting node to the completion node.
B) is a combination of all paths.
C) is the shortest path.
D) is the longest path.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
34
To calculate an activity's latest finish time, you should consider its
A) predecessors' latest finish times
B) predecessors' latest start times
C) successors' earliest start times
D) successors' latest start times
A) predecessors' latest finish times
B) predecessors' latest start times
C) successors' earliest start times
D) successors' latest start times

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
35
For an activity with more than one immediate predecessor activity, which of the following is used to compute its earliest finish (EF) time?
A) the largest EF among the immediate predecessors.
B) the average EF among the immediate predecessors.
C) the largest LF among the immediate predecessors.
D) the difference in EF among the immediate predecessors.
A) the largest EF among the immediate predecessors.
B) the average EF among the immediate predecessors.
C) the largest LF among the immediate predecessors.
D) the difference in EF among the immediate predecessors.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
36
Slack equals
A) LF − EF.
B) EF − LF.
C) EF − LS.
D) LF − ES.
A) LF − EF.
B) EF − LF.
C) EF − LS.
D) LF − ES.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
37
To determine how to crash activity times
A) normal activity costs and costs under maximum crashing must be known.
B) shortest times with crashing must be known.
C) realize that new paths may become critical.
D) All of the alternatives are true.
A) normal activity costs and costs under maximum crashing must be known.
B) shortest times with crashing must be known.
C) realize that new paths may become critical.
D) All of the alternatives are true.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
38
PERT and CPM
A) are most valuable when a small number of activities must be scheduled.
B) have different features and are not applied to the same situation.
C) do not require a chronological relationship among activities.
D) have been combined to develop a procedure that uses the best of each.
A) are most valuable when a small number of activities must be scheduled.
B) have different features and are not applied to the same situation.
C) do not require a chronological relationship among activities.
D) have been combined to develop a procedure that uses the best of each.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
39
The normal distribution tends to be a better approximation of the distribution of total time for shorter projects where the critical path has relatively few activities.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
40
Which of the following is always true about a critical activity?
A) LS = EF.
B) LF = LS.
C) ES = LS.
D) EF = ES.
A) LS = EF.
B) LF = LS.
C) ES = LS.
D) EF = ES.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
41
A cookie recipe gives the following numbered steps.
1.Preheat oven.
2.Grease cookie sheets.
3.Cream shortening and sugar.
4.Add eggs and flavoring.
5.Measure and sift dry ingredients.
6.Add dry ingredients to mixture.
7.Drop by spoonfuls onto sheets and bake for 10 minutes.
Although the steps are numbered, they do not always reflect immediate precedence relationships. Develop a table that lists the immediate predecessors for each activity.
1.Preheat oven.
2.Grease cookie sheets.
3.Cream shortening and sugar.
4.Add eggs and flavoring.
5.Measure and sift dry ingredients.
6.Add dry ingredients to mixture.
7.Drop by spoonfuls onto sheets and bake for 10 minutes.
Although the steps are numbered, they do not always reflect immediate precedence relationships. Develop a table that lists the immediate predecessors for each activity.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
42
In PERT, the activity duration time is equal to the
A) pessimistic time.
B) optimistic time.
C) most likely time.
D) mean duration.
A) pessimistic time.
B) optimistic time.
C) most likely time.
D) mean duration.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
43
The critical path for this network is A - E - F and the project completion time is 22 weeks. 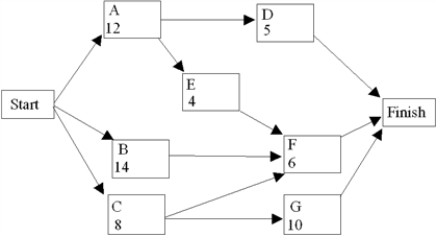
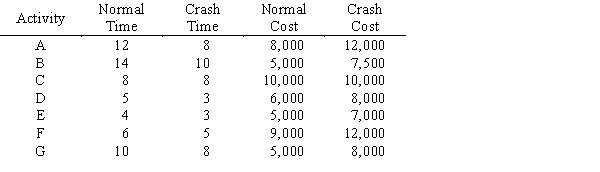
If a deadline of 17 weeks is imposed, give the linear programming model for the crashing decision.


If a deadline of 17 weeks is imposed, give the linear programming model for the crashing decision.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
44
Use the following network of related activities with their duration times (weeks) to complete a row for each activity under the column headings below. 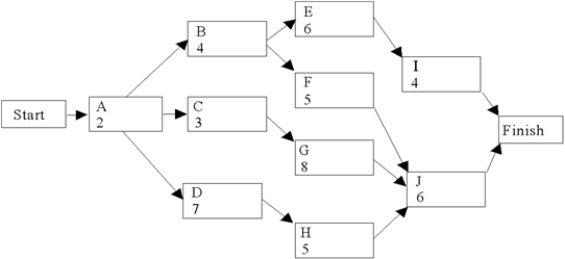
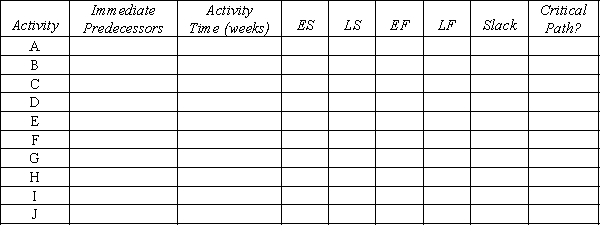



Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
45
From this schedule of activities, draw the PERT/CPM network. 


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
46
National Oil Company (NATOCO) must plan the shutdown of its Houston refinery for routine preventive maintenance. Each hour of downtime is lost production time and is very costly, so NATOCO wants the maintenance project completed in 22 hours. The PERT network below shows the precedence relationships of the activities involved in the project. The table gives the activity times and costs under normal operations and maximum crashing.
?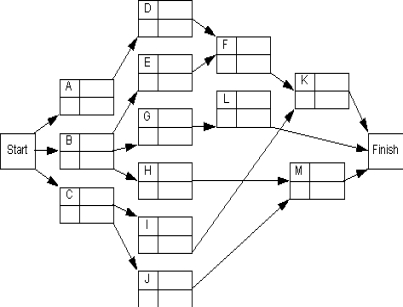 ?
?
NATOCO wants to know the minimum cost of completing the maintenance project within the 22-hour period. Formulate and solve a linear program that will yield this information.
???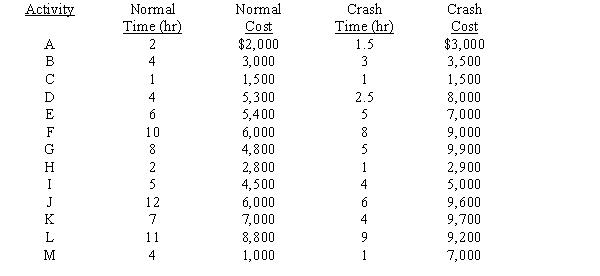 ?
?
?
 ?
?NATOCO wants to know the minimum cost of completing the maintenance project within the 22-hour period. Formulate and solve a linear program that will yield this information.
???
 ?
?
Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
47
From this PERT/CPM network, determine the list of activities and their predecessors.
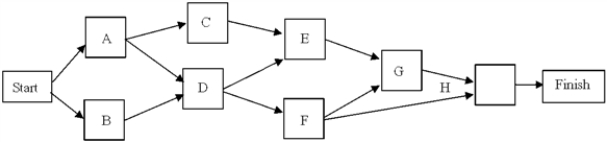


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
48
Joseph King has ambitions to be mayor of Williston, North Dakota. Joe has determined the breakdown of the steps to the nomination and has estimated normal and crash costs and times for the campaign as follows (times are in weeks). 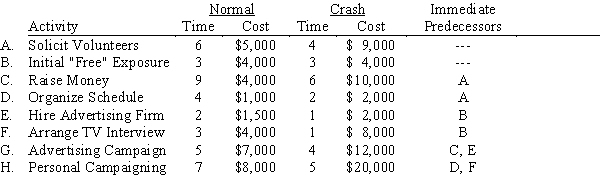
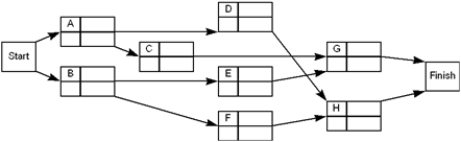
Joe King is not a wealthy man and would like to organize a 16-week campaign at minimum cost. Write and solve a linear program to accomplish this task.


Joe King is not a wealthy man and would like to organize a 16-week campaign at minimum cost. Write and solve a linear program to accomplish this task.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
49
A project network is shown below. Use a forward and a backward pass to determine the critical path, and then fill out the table below. Activity times are in weeks. 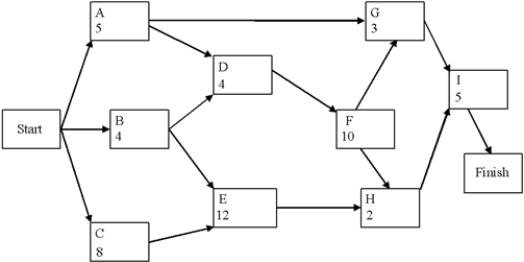
 Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in fewer than 25 weeks more or less than 50%?
Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in fewer than 25 weeks more or less than 50%?

 Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in fewer than 25 weeks more or less than 50%?
Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in fewer than 25 weeks more or less than 50%?
Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
50
For the project represented below, determine the earliest and latest start and finish times for each activity as well as the expected overall completion time. 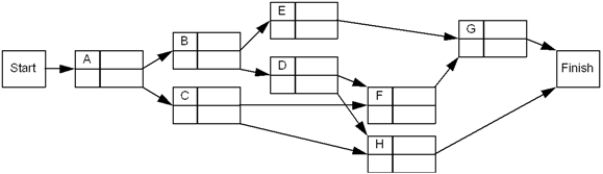
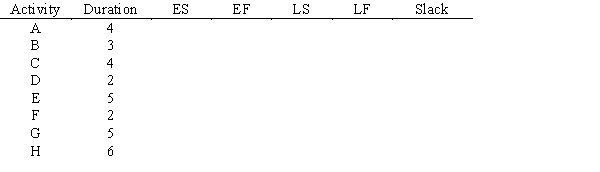



Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
51
A project network is shown below. Use a forward and a backward pass to determine the critical path, and then fill out the table below. Activity times are in weeks. 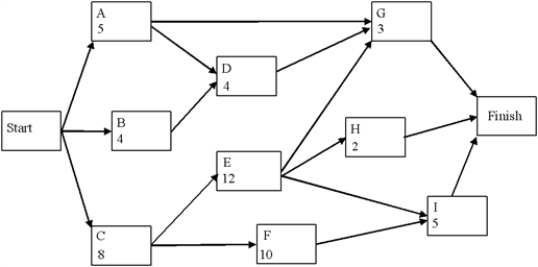
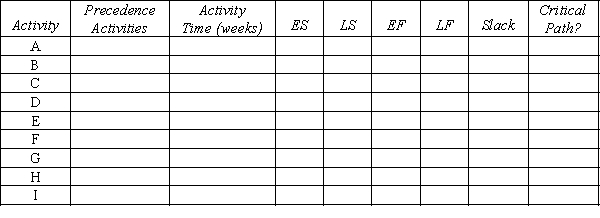 Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in more than 28 weeks more or less than 50%?
Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in more than 28 weeks more or less than 50%?

 Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in more than 28 weeks more or less than 50%?
Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in more than 28 weeks more or less than 50%?
Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
52
A project consists of five activities. Naturally the paint mixing precedes the painting activities. Also, both ceiling painting and floor sanding must be done prior to floor buffing. 
a.
Construct the PERT/CPM network for this problem.
b.
What is the expected completion time of this project?
c.
What is the probability that the project can be completed within 9 hr.?

a.
Construct the PERT/CPM network for this problem.
b.
What is the expected completion time of this project?
c.
What is the probability that the project can be completed within 9 hr.?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
53
Marcy Fetter, a staff analyst at the Los Angeles plant of Computer Products Corporation, is assigned to the team that is developing the process design for producing an RFID sensor. The corporate planning group in San Jose, California has contacted her and has asked how confident the design group is about completing the project in 60 days. She has developed these estimated time durations in days for the project:
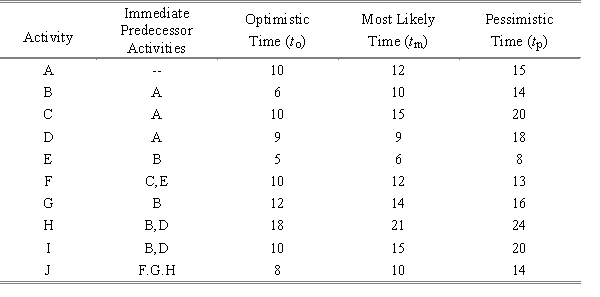
a. Compute the expected time and variance for each activity.
b. Determine the critical path and the expected duration of the project.
c. What is the probability that the project will take longer than 58 days to complete?
d. Which path in the project network offers the greatest risk of overrunning a new deadline of 56 days?

a. Compute the expected time and variance for each activity.
b. Determine the critical path and the expected duration of the project.
c. What is the probability that the project will take longer than 58 days to complete?
d. Which path in the project network offers the greatest risk of overrunning a new deadline of 56 days?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
54
Use the following network of related activities with their duration times (weeks) to complete a row for each activity under the column headings below. 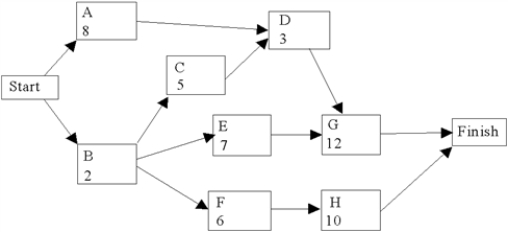



Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
55
Consider a project that has been modeled as follows: 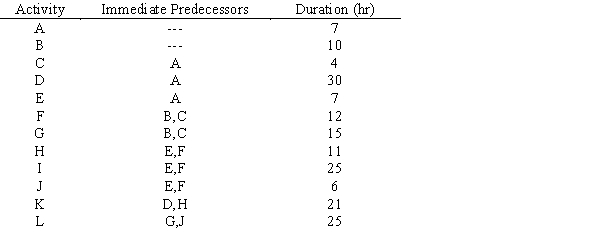
a.
Draw the PERT/CPM network for this project and determine project's expected completion time and its critical path.
b.
Can activities E and G be performed simultaneously without delaying the minimum project completion time?
c.
Can one person perform A, G, and I without delaying the project?
d.
By how much can activities G and L be delayed without delaying the entire project?
e.
How much would the project be delayed if activity G was delayed by 7 hours and activity L was delayed by 4 hours? Explain.

a.
Draw the PERT/CPM network for this project and determine project's expected completion time and its critical path.
b.
Can activities E and G be performed simultaneously without delaying the minimum project completion time?
c.
Can one person perform A, G, and I without delaying the project?
d.
By how much can activities G and L be delayed without delaying the entire project?
e.
How much would the project be delayed if activity G was delayed by 7 hours and activity L was delayed by 4 hours? Explain.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
56
Given the following network with activities and times estimated in days, 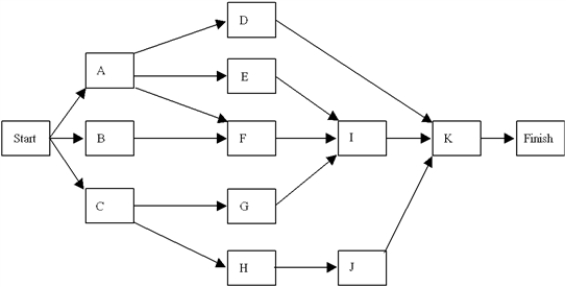
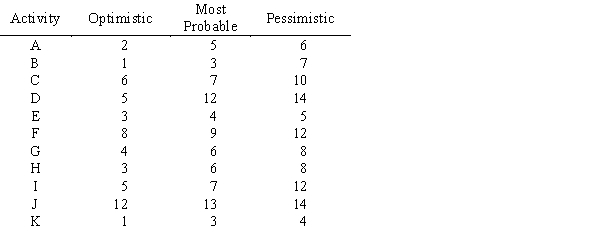
a.
What are the critical path activities?
b.
What is the expected time to complete the project?
c.
What is the probability the project will take more than 28 days to complete?


a.
What are the critical path activities?
b.
What is the expected time to complete the project?
c.
What is the probability the project will take more than 28 days to complete?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
57
Consider the following PERT/CPM network with estimated times in weeks. The project is scheduled to begin on May 1. 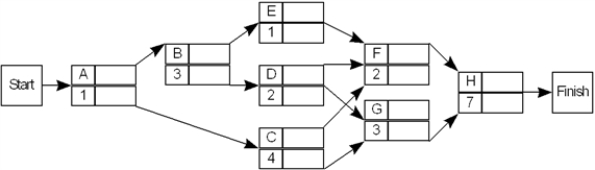 The three-time estimate approach was used to calculate the expected times and the following table gives the variance for each activity:
The three-time estimate approach was used to calculate the expected times and the following table gives the variance for each activity: 
a.
Give the expected project completion date and the critical path.
b.
By what date are you 99% sure the project will be completed?
 The three-time estimate approach was used to calculate the expected times and the following table gives the variance for each activity:
The three-time estimate approach was used to calculate the expected times and the following table gives the variance for each activity: 
a.
Give the expected project completion date and the critical path.
b.
By what date are you 99% sure the project will be completed?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
58
A senior MIS design class project team has developed the following schedule of activities for their project, using their best estimate of completion times. Both written and oral reports are required. Draw the project network. Can they complete the project in the 38 class days remaining until the end of the semester? 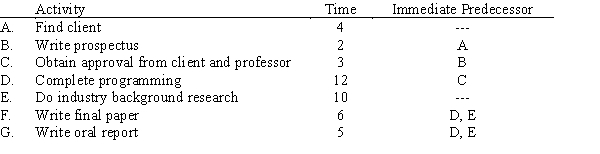


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
59
The main difference between CPM and PERT is
A) the use of different activity time estimates.
B) PERT analysis is less expensive to conduct.
C) PERT lends itself to computerization while CPM networks must be constructed manually.
D) CPM integrates time and cost performance while PERT is based solely on time performance.
A) the use of different activity time estimates.
B) PERT analysis is less expensive to conduct.
C) PERT lends itself to computerization while CPM networks must be constructed manually.
D) CPM integrates time and cost performance while PERT is based solely on time performance.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck


