Deck 4: Systems of Linear Equations and Inequalities
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/113
Play
Full screen (f)
Deck 4: Systems of Linear Equations and Inequalities
1
Solve the system by graphing.
3x + 3y = 27 2x - 2y = -2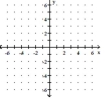
A)
B)
C)
D) no solution
3x + 3y = 27 2x - 2y = -2

A)
B)
C)
D) no solution
C
2
Use the substitution method to solve the system.
x + 6y = 6 4x - 5y = -5
A)(1, 1)
B)(0, 1)
C)(0, 0)
D)(1, 0)
x + 6y = 6 4x - 5y = -5
A)(1, 1)
B)(0, 1)
C)(0, 0)
D)(1, 0)
B
3
Use the substitution method to solve the system.
6x + 5y = -12 -4x - 2y = 0
A)(3, -5)
B)(3, -6)
C)(2, -5)
D)No solution
6x + 5y = -12 -4x - 2y = 0
A)(3, -5)
B)(3, -6)
C)(2, -5)
D)No solution
B
4
Use the substitution method to solve the system.
x + 7y = 4 6x + 8y = 24
A)(5, 4)
B)(4, 0)
C)(-4, -1)
D)No solution
x + 7y = 4 6x + 8y = 24
A)(5, 4)
B)(4, 0)
C)(-4, -1)
D)No solution

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
5
Solve the system by graphing.
x = -y y + x = 6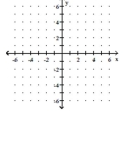
A) no solution
B) infinite number of solutions
C)
D)
x = -y y + x = 6

A) no solution
B) infinite number of solutions
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
6
Determine whether the given ordered pair is a solution to the system of equations.
A)
B)
A)
B)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
7
Determine whether the given ordered pair is a solution to the system of equations.
(-6, -4) 4x + y = -20
2x + 4y = 4
A)No
B)Yes
(-6, -4) 4x + y = -20
2x + 4y = 4
A)No
B)Yes

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
8
Use the substitution method to solve the system.
8x + 7y = -8 2x + 3y = -2
A)(-1, 0)
B)(-1, 1)
C)(-2, 1)
D)No solution
8x + 7y = -8 2x + 3y = -2
A)(-1, 0)
B)(-1, 1)
C)(-2, 1)
D)No solution

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
9
Determine whether the given ordered pair is a solution to the system of equations.
(-4, -5) 4x + y = -21
3x + 4y = -32
A)No
B)Yes
(-4, -5) 4x + y = -21
3x + 4y = -32
A)No
B)Yes

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the system by graphing.
3x - 2y = 4 -6x + 4y = 7
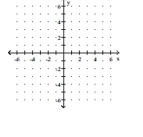
A)
B) no solution
C) infinite number of solutions
D)
3x - 2y = 4 -6x + 4y = 7

A)
B) no solution
C) infinite number of solutions
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the system by graphing.
y - 3x = 4 2y = 6x + 8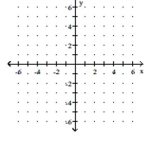
A) no solution
B)
C) infinite number of solutions
D)
y - 3x = 4 2y = 6x + 8

A) no solution
B)
C) infinite number of solutions
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the system by graphing.
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
13
Solve the system by graphing.
3x + y = 12 9x + 3y = 36
A) infinite number of solutions
B) no solution
C)
D)
3x + y = 12 9x + 3y = 36

A) infinite number of solutions
B) no solution
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
14
Use the substitution method to solve the system.
8x + y = 0 -8x + y = -16
A)(-1, -8)
B)(1, -8)
C)(1, 16)
D)(-1, 8)
8x + y = 0 -8x + y = -16
A)(-1, -8)
B)(1, -8)
C)(1, 16)
D)(-1, 8)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
15
Determine whether the given ordered pair is a solution to the system of equations.
(5, 6) 2x = -4 - y
3x = -3 - 2y
A)Yes
B)No
(5, 6) 2x = -4 - y
3x = -3 - 2y
A)Yes
B)No

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
16
Use the substitution method to solve the system.
x - 7y = 36 5x - 8y = 45
A)(1, -5)
B)(-1, -4)
C)(0, -4)
D)No solution
x - 7y = 36 5x - 8y = 45
A)(1, -5)
B)(-1, -4)
C)(0, -4)
D)No solution

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
17
Solve the system by graphing.
A) infinite number of solutions
B)
C)
D) no solution

A) infinite number of solutions
B)
C)
D) no solution

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
18
Determine whether the given ordered pair is a solution to the system of equations.
A) No
B) Yes
A) No
B) Yes

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the system by graphing.
2x + y = -3 2x + 2y = 2
A)
B)
C)
D)
2x + y = -3 2x + 2y = 2

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
20
Use the substitution method to solve the system.
x - 4y = 8 -3x - 3y = 6
A)(2, 0)
B)(0, -2)
C)(1, -3)
D)No solution
x - 4y = 8 -3x - 3y = 6
A)(2, 0)
B)(0, -2)
C)(1, -3)
D)No solution

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
21
Use the substitution method to solve the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
22
Use the substitution method to solve the system.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
23
If possible, solve the system of equations. Use any method. If there is not a unique solution to a system, say why.
A)
B) No solution; inconsistent system of equations
C) Infinite number of solutions; dependent equations
D)
A)
B) No solution; inconsistent system of equations
C) Infinite number of solutions; dependent equations
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
24
If possible, solve the system of equations. Use any method. If there is not a unique solution to a system, say why.
A) No solution; inconsistent system of equations
B) ,)
C)
D) \((\,)
A) No solution; inconsistent system of equations
B) ,)
C)
D) \((\,)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
25
If possible, solve the system of equations. Use any method. If there is not a unique solution to a system, say why.
4x = 45 - 9y -2x + 7y = -11
A)(8, 2)
B)No solution; inconsistent system of equations
C)(9, 1)
D)(9, 2)
4x = 45 - 9y -2x + 7y = -11
A)(8, 2)
B)No solution; inconsistent system of equations
C)(9, 1)
D)(9, 2)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
26
Find the solution to the system by addition (elimination) method.
5x + 54y = 54 3x - 6y = -6
A)(1, 1)
B)(0, 1)
C)(0, 0)
D)(1, 0)
5x + 54y = 54 3x - 6y = -6
A)(1, 1)
B)(0, 1)
C)(0, 0)
D)(1, 0)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
27
Choose the most appropriate method for solving the system of equations. Do not solve.
x + y = 3050 4x + 5y = 8170
A)Addition
B)Substitution
x + y = 3050 4x + 5y = 8170
A)Addition
B)Substitution

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
28
If possible, solve the system of equations. Use any method. If there is not a unique solution to a system, say why.
-8x + 6y = -80 -3x - 9y = 60
A)(4, -8)
B)(-4, -7)
C)(3, -7)
D)No solution; inconsistent system of equations
-8x + 6y = -80 -3x - 9y = 60
A)(4, -8)
B)(-4, -7)
C)(3, -7)
D)No solution; inconsistent system of equations

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
29
Solve.
A couple have bought a new house and are comparing quotes from two moving companies for moving their furniture. Company A charges for the truck and per hour for the movers. Company B charges for the truck and per hour for the movers. Create a cost equation for each company where is the total cost and is the number of hours of labor. Write a system of equations.
A)
B)
C)
D)
A couple have bought a new house and are comparing quotes from two moving companies for moving their furniture. Company A charges for the truck and per hour for the movers. Company B charges for the truck and per hour for the movers. Create a cost equation for each company where is the total cost and is the number of hours of labor. Write a system of equations.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
29
Find the solution to the system by addition (elimination) method.
A) , )
B) , )
C)
D) No solution
A) , )
B) , )
C)
D) No solution

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
30
Find the solution to the system by addition (elimination) method.
x + y = -6 x - y = 14
A)(6, 4)
B)(4, 10)
C)(4, -10)
D)(6, -10)
x + y = -6 x - y = 14
A)(6, 4)
B)(4, 10)
C)(4, -10)
D)(6, -10)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
31
If possible, solve the system of equations. Use any method. If there is not a unique solution to a system, say why.
A) No solution; inconsistent system of equations
B) Infinite number of solutions; dependent equations
C)
D)
A) No solution; inconsistent system of equations
B) Infinite number of solutions; dependent equations
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
32
Choose the most appropriate method for solving the system of equations. Do not solve.
2x - 3y = 19 -5x + 7y = 28
A)Addition
B)Substitution
2x - 3y = 19 -5x + 7y = 28
A)Addition
B)Substitution

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
33
Solve.
Juanita is having her yard landscaped. She obtained an estimate from two landscaping companies. Company A gave an estimate of $180 for materials and equipment rental plus $60 per hour for labor. Company B gave and
Estimate of $300 for materials and equipment rental plus $45 per hour for labor. Create a cost equation for each
Company where y is the total cost of the landscaping and x is the number of hours of labor. Determine how
Many hours of labor will be required for the two companies to cost the same.
A)7 hours
B)11 hours
C)8 hours
D)12 hours
Juanita is having her yard landscaped. She obtained an estimate from two landscaping companies. Company A gave an estimate of $180 for materials and equipment rental plus $60 per hour for labor. Company B gave and
Estimate of $300 for materials and equipment rental plus $45 per hour for labor. Create a cost equation for each
Company where y is the total cost of the landscaping and x is the number of hours of labor. Determine how
Many hours of labor will be required for the two companies to cost the same.
A)7 hours
B)11 hours
C)8 hours
D)12 hours

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
34
Find the solution to the system by addition (elimination) method.
6x + 5y = -19 -6x - 11y = 49
A)(6, 5)
B)(1, -5)
C)(-1, 5)
D)(-6, - 5)
6x + 5y = -19 -6x - 11y = 49
A)(6, 5)
B)(1, -5)
C)(-1, 5)
D)(-6, - 5)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
35
If possible, solve the system of equations. Use any method. If there is not a unique solution to a system, say why.
B)
A) , )
D) No solution; inconsistent system of equations
B)
A) , )
D) No solution; inconsistent system of equations

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
35
Find the solution to the system by addition (elimination) method.
2x + 8y = -6 2x + 2y = 24
A)(-17, 8)
B)(-17, 2)
C)(-5, 17)
D)(17, -5)
2x + 8y = -6 2x + 2y = 24
A)(-17, 8)
B)(-17, 2)
C)(-5, 17)
D)(17, -5)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
36
Find the solution to the system by addition (elimination) method.
A)
B)
C)
D) No solution
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
37
If possible, solve the system of equations. Use any method. If there is not a unique solution to a system, say why.
A) \quad )\)
B) ,\quad )\)
C) No solution; inconsistent system of equations
D)
A) \quad )\)
B) ,\quad )\)
C) No solution; inconsistent system of equations
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
38
If possible, solve the system of equations. Use any method. If there is not a unique solution to a system, say why.
A)
B)
C) Infinite number of solutions; dependent equations
D) No solution; inconsistent system of equations
A)
B)
C) Infinite number of solutions; dependent equations
D) No solution; inconsistent system of equations

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
39
Find the solution to the system by addition (elimination) method.
A)
B)
C)
D) No solution
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
40
Find the solution to the system by addition (elimination) method.
2x + 10y = -56 9x + 2y = 49
A)(9, -9)
B)(7, -7)
C)(-7, 7)
D)(-2, 7)
2x + 10y = -56 9x + 2y = 49
A)(9, -9)
B)(7, -7)
C)(-7, 7)
D)(-2, 7)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
41
Solve.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
42
Solve.
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
43
Solve.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
44
Solve.
A)
B) Yes
A)
B) Yes

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
45
Solve.
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
46
Solve.
A)
B) Yes
A)
B) Yes

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
47
Solve.
A) Yes
B)
A) Yes
B)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
48
Solve.
x + y + z = 1 x - y + 2z = 8
2x + y + z = -2
(5, -1, -3)
A)Yes
B)No
x + y + z = 1 x - y + 2z = 8
2x + y + z = -2
(5, -1, -3)
A)Yes
B)No

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
49
Solve.
A) No
B) Yes
A) No
B) Yes

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
50
Solve.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
51
Find the solution to the system of equations. Round the answer to five decimal places

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
52
Solve.
A) No
B) Yes
A) No
B) Yes

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
54
Solve.
A) Yes
B)
A) Yes
B)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
56
Solve.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
57
Solve.
A)
B) Yes
A)
B) Yes

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the system of equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
58
Solve.
A) , )
В) ,
C) ,)
D) )
A) , )
В) ,
C) ,)
D) )

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
59
Solve.
A) No solution; inconsistent system of equations
B) Infinite number of solutions; dependent equations
C)
D)
A) No solution; inconsistent system of equations
B) Infinite number of solutions; dependent equations
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
60
Solve.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the problem.
A textile company has specific dyeing and drying times for its different cloths. A roll of Cloth A requires 55 minutes of dyeing time and 45 minutes of drying time. A roll of Cloth B requires 60 minutes of dyeing time and
30 minutes of drying time. The production division allocates 2280 minutes of dyeing time and 1560 minutes of
Drying time for the week. How many rolls of each cloth can be dyed and dried?
A)13 rolls of Cloth A, 28 rolls of Cloth B
B)24 rolls of Cloth A, 16 rolls of Cloth B
C)2 rolls of Cloth A, 49 rolls of Cloth B
D)13 rolls of Cloth A, 40 rolls of Cloth B
A textile company has specific dyeing and drying times for its different cloths. A roll of Cloth A requires 55 minutes of dyeing time and 45 minutes of drying time. A roll of Cloth B requires 60 minutes of dyeing time and
30 minutes of drying time. The production division allocates 2280 minutes of dyeing time and 1560 minutes of
Drying time for the week. How many rolls of each cloth can be dyed and dried?
A)13 rolls of Cloth A, 28 rolls of Cloth B
B)24 rolls of Cloth A, 16 rolls of Cloth B
C)2 rolls of Cloth A, 49 rolls of Cloth B
D)13 rolls of Cloth A, 40 rolls of Cloth B

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
62
Solve using a system of three linear equations.
A basketball player scored 32 points in a game. The number of three-point field goals the player made was 24 less than three times the number of free throws (each worth 1 point). Twice the number of two-point field goals
The player made was 11 more than the number of three-point field goals made. Find the number of free-throws,
Two-point field goals, and three-point field goals that the player made in the game.
A)9 free throws; 7 two-point field goals; 3 three-point field goals
B)9 free throws; 3 two-point field goals; 7 three-point field goals
C)10 free throws; 7 two-point field goals; 6 three-point field goals
D)9 free throws; 8 two-point field goals; 5 three-point field goals
A basketball player scored 32 points in a game. The number of three-point field goals the player made was 24 less than three times the number of free throws (each worth 1 point). Twice the number of two-point field goals
The player made was 11 more than the number of three-point field goals made. Find the number of free-throws,
Two-point field goals, and three-point field goals that the player made in the game.
A)9 free throws; 7 two-point field goals; 3 three-point field goals
B)9 free throws; 3 two-point field goals; 7 three-point field goals
C)10 free throws; 7 two-point field goals; 6 three-point field goals
D)9 free throws; 8 two-point field goals; 5 three-point field goals

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the system of equations.
A)
B)
C) No solution
D) Infinite number of solutions; dependent equations
A)
B)
C) No solution
D) Infinite number of solutions; dependent equations

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the problem.
A tour group split into two groups when waiting in line for food at a fast food counter. The first group bought 8 slices of pizza and 7 soft drinks for $42.00. The second group bought 7 slices of pizza and 6 soft drinks for $
36)57. How much does one slice of pizza cost?
A)$1.44 per slice of pizza
B)$1.94 per slice of pizza
C)$3.49 per slice of pizza
D)$3.99 per slice of pizza
A tour group split into two groups when waiting in line for food at a fast food counter. The first group bought 8 slices of pizza and 7 soft drinks for $42.00. The second group bought 7 slices of pizza and 6 soft drinks for $
36)57. How much does one slice of pizza cost?
A)$1.44 per slice of pizza
B)$1.94 per slice of pizza
C)$3.49 per slice of pizza
D)$3.99 per slice of pizza

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the system of equations.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the problem.
A vendor sells hot dogs and bags of potato chips. A customer buys 4 hot dogs and 4 bags of potato chips for $7.00. Another customer buys 3 hot dogs and 4 bags of potato chips for $6.00. Find the cost of each item.
A)$0.75 for a hot dog; $1.00 for a bag of potato chips
B)$1.25 for a hot dog; $1.00 for a bag of potato chips
C)$1.00 for a hot dog; $0.75 for a bag of potato chips
D)$1.00 for a hot dog; $1.00 for a bag of potato chips
A vendor sells hot dogs and bags of potato chips. A customer buys 4 hot dogs and 4 bags of potato chips for $7.00. Another customer buys 3 hot dogs and 4 bags of potato chips for $6.00. Find the cost of each item.
A)$0.75 for a hot dog; $1.00 for a bag of potato chips
B)$1.25 for a hot dog; $1.00 for a bag of potato chips
C)$1.00 for a hot dog; $0.75 for a bag of potato chips
D)$1.00 for a hot dog; $1.00 for a bag of potato chips

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the system of equations.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the problem.
Sandy Brondello scored 24 points in a recent basketball game without making any 3-point shots. She scored 16 times, making several free throws worth 1 point each and several field goals worth two points each. How many
Free throws did she make? How many 2-point field goals did she make?
A)10 free throws, 7 field goals
B)6 free throws, 10 field goals
C)9 free throws, 7 field goals
D)8 free throws, 8 field goals
Sandy Brondello scored 24 points in a recent basketball game without making any 3-point shots. She scored 16 times, making several free throws worth 1 point each and several field goals worth two points each. How many
Free throws did she make? How many 2-point field goals did she make?
A)10 free throws, 7 field goals
B)6 free throws, 10 field goals
C)9 free throws, 7 field goals
D)8 free throws, 8 field goals

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
67
Solve using a system of three linear equations.
A ceramics workshop makes wreaths, trees, and sleighs for sale at Christmas. A wreath takes 3 hours to prepare, 2 hours to paint, and 9 hours to fire. A tree takes 14 hours to prepare, 3 hours to paint, and 4 hours to
Fire. A sleigh takes 4 hours to prepare, 16 hours to paint, and 7 hours to fire. If the workshop has 109 hours for
Prep time, 81 hours for painting, and 122 hours for firing, How many of each can be made?
A)3 wreaths, 9 trees, 5 sleighs
B)9 wreaths, 5 trees, 3 sleighs
C)5 wreaths, 3 trees, 9 sleighs
D)10 wreaths, 6 trees, 4 sleighs
A ceramics workshop makes wreaths, trees, and sleighs for sale at Christmas. A wreath takes 3 hours to prepare, 2 hours to paint, and 9 hours to fire. A tree takes 14 hours to prepare, 3 hours to paint, and 4 hours to
Fire. A sleigh takes 4 hours to prepare, 16 hours to paint, and 7 hours to fire. If the workshop has 109 hours for
Prep time, 81 hours for painting, and 122 hours for firing, How many of each can be made?
A)3 wreaths, 9 trees, 5 sleighs
B)9 wreaths, 5 trees, 3 sleighs
C)5 wreaths, 3 trees, 9 sleighs
D)10 wreaths, 6 trees, 4 sleighs

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the problem.
Kelly is a partner in an Internet-based seed and garden supply business. The company offers a blend of exotic wildflower seeds for $105 per pound and a blend of common wildflower seeds for $15 per pound. Kelly is
Creating a medium-price product by mixing together 26 pounds of the more expensive blend with 10 pounds of
The less expensive blend. What will be the price per pound for the new blend? (Round to the nearest cent, if
Necessary.)
A)$12.00 per pound
B)$40.00 per pound
C)$24.00 per pound
D)$80.00 per pound
Kelly is a partner in an Internet-based seed and garden supply business. The company offers a blend of exotic wildflower seeds for $105 per pound and a blend of common wildflower seeds for $15 per pound. Kelly is
Creating a medium-price product by mixing together 26 pounds of the more expensive blend with 10 pounds of
The less expensive blend. What will be the price per pound for the new blend? (Round to the nearest cent, if
Necessary.)
A)$12.00 per pound
B)$40.00 per pound
C)$24.00 per pound
D)$80.00 per pound

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
69
Graph the system of inequalities.
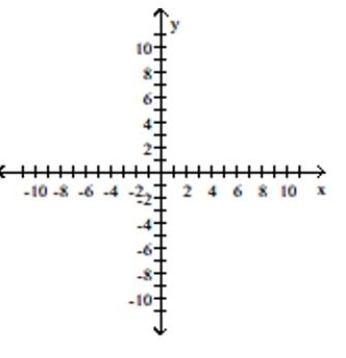 A)
A)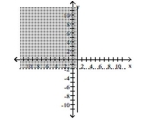
B)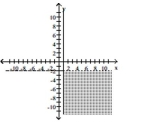
C)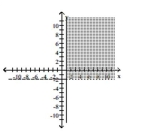
D)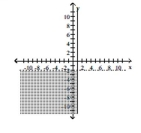
 A)
A)
B)

C)

D)


Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the problem.
A twin-engined aircraft can fly 768 miles from city A to city B in 3 hours with the wind and make the return trip in 8 hours against the wind. What is the speed of the wind?
A)112 mph
B)96 mph
C)80 mph
D)64 mph
A twin-engined aircraft can fly 768 miles from city A to city B in 3 hours with the wind and make the return trip in 8 hours against the wind. What is the speed of the wind?
A)112 mph
B)96 mph
C)80 mph
D)64 mph

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the problem.
Corey has found that his new car gets 34 miles per gallon on the highway and 29 miles per gallon in the city. He recently drove 286 miles on 9 gallons of gasoline. How many miles did he drive on the highway? How many
Miles did he drive in the city?
A)145 miles on the highway, 141 miles in the city
B)170 miles on the highway, 116 miles in the city
C)155 miles on the highway, 131 miles in the city
D)160 miles on the highway, 126 miles in the city
Corey has found that his new car gets 34 miles per gallon on the highway and 29 miles per gallon in the city. He recently drove 286 miles on 9 gallons of gasoline. How many miles did he drive on the highway? How many
Miles did he drive in the city?
A)145 miles on the highway, 141 miles in the city
B)170 miles on the highway, 116 miles in the city
C)155 miles on the highway, 131 miles in the city
D)160 miles on the highway, 126 miles in the city

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
72
Solve using a system of three linear equations.
A total of 384 people attend a community theatre performance. The admission prices were $10.00 for adults, $8.00 for students, and $9.00 for senior citizens. The ticket sales totaled $3590. At the theatre's next board
Meeting, the finance manager proposed that for the next play they raise prices to $11.00 for adults, $8.50 for
Students, and $9.50 for senior citizens. He said that if the exact same number of people attend the next
Performance, the ticket sales would be $3886. How many adults, students, and senior citizens attended the
Play?
A)196 adults, 78 students, 110 senior citizens
B)200 adults, 80 students, 104 senior citizens
C)204 adults, 72 students, 108 senior citizens
D)208 adults, 74 students, 102 senior citizens
A total of 384 people attend a community theatre performance. The admission prices were $10.00 for adults, $8.00 for students, and $9.00 for senior citizens. The ticket sales totaled $3590. At the theatre's next board
Meeting, the finance manager proposed that for the next play they raise prices to $11.00 for adults, $8.50 for
Students, and $9.50 for senior citizens. He said that if the exact same number of people attend the next
Performance, the ticket sales would be $3886. How many adults, students, and senior citizens attended the
Play?
A)196 adults, 78 students, 110 senior citizens
B)200 adults, 80 students, 104 senior citizens
C)204 adults, 72 students, 108 senior citizens
D)208 adults, 74 students, 102 senior citizens

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
73
Solve using a system of three linear equations.
A real estate investor is examining a triangular plot of land. She measures each angle of the field. The sum of the first and second angles is 114° more than the measure of the third angle. If the measure of the third angle is
Subtracted from the measure of the second angle, the result is twice the measure of the first angle. Find the
Measure of each angle. (Note: The sum of the angles of a triangle is 180°.)
A)First angle is 42°, second angle is 111°, third angle is 27°
B)First angle is 38°, second angle is 109°, third angle is 33°
C)First angle is 36°, second angle is 109°, third angle is 31°
D)First angle is 44°, second angle is 105°, third angle is 31°
A real estate investor is examining a triangular plot of land. She measures each angle of the field. The sum of the first and second angles is 114° more than the measure of the third angle. If the measure of the third angle is
Subtracted from the measure of the second angle, the result is twice the measure of the first angle. Find the
Measure of each angle. (Note: The sum of the angles of a triangle is 180°.)
A)First angle is 42°, second angle is 111°, third angle is 27°
B)First angle is 38°, second angle is 109°, third angle is 33°
C)First angle is 36°, second angle is 109°, third angle is 31°
D)First angle is 44°, second angle is 105°, third angle is 31°

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
74
Solve using a system of three linear equations.
A deli sells three sizes of roast beef sandwiches: the small roast beef sandwich contains 4 ounces of meat and sells for $3.00; the regular roast beef sandwich contains 7 ounces of meat and sells for $3.50; and the large
Roast beef sandwich contains 9 ounces of meat and sells for $4.00. A customer requests a selection of each size
For a reception. She and the manager agree on a combination of 54 sandwiches made from 20 pounds 2 ounces
Of roast beef for a total cost of $181. How many of each size sandwich will be in this combination? (Note: 1
Pound = 16 ounces)
A)20 small sandwiches, 18 medium sandwiches, 16 large sandwiches.
B)22 small sandwiches, 28 medium sandwiches, 4 large sandwiches.
C)24 small sandwiches, 22 medium sandwiches, 8 large sandwiches.
D)26 small sandwiches, 16 medium sandwiches, 12 large sandwiches.
A deli sells three sizes of roast beef sandwiches: the small roast beef sandwich contains 4 ounces of meat and sells for $3.00; the regular roast beef sandwich contains 7 ounces of meat and sells for $3.50; and the large
Roast beef sandwich contains 9 ounces of meat and sells for $4.00. A customer requests a selection of each size
For a reception. She and the manager agree on a combination of 54 sandwiches made from 20 pounds 2 ounces
Of roast beef for a total cost of $181. How many of each size sandwich will be in this combination? (Note: 1
Pound = 16 ounces)
A)20 small sandwiches, 18 medium sandwiches, 16 large sandwiches.
B)22 small sandwiches, 28 medium sandwiches, 4 large sandwiches.
C)24 small sandwiches, 22 medium sandwiches, 8 large sandwiches.
D)26 small sandwiches, 16 medium sandwiches, 12 large sandwiches.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
75
Solve using a system of three linear equations.
Three shrimp boats supply the shrimp wholesalers on Hilton Head with fresh catch. The Annabelle takes 50% of its catch to Hudson's, 20% to Captain J's, and 30% to Mainstreet. The Curly Q takes 40% of its catch to Hudson's,
40% to Captain J's, and 20% to Mainstreet. The SloJoe takes 30% of its catch to Hudson's, 40% to Captain J's, and
30% to Mainstreet. One week Hudson's received 240.2 pounds of shrimp, Captain J's received 203.8 pounds, and
Mainstreet received 158 pounds. How many pounds of shrimp did each boat catch?
A)Annabelle 191 lbs, Curly Q 185 lbs, SloJoe 226 lbs
B)Annabelle 191 lbs, Curly Q 226 lbs, SloJoe 185 lbs
C)Annabelle 185 lbs, Curly Q 226 lbs, SloJoe 191 lbs
D)Annabelle 226 lbs, Curly Q 191 lbs, SloJoe 185 lbs
Three shrimp boats supply the shrimp wholesalers on Hilton Head with fresh catch. The Annabelle takes 50% of its catch to Hudson's, 20% to Captain J's, and 30% to Mainstreet. The Curly Q takes 40% of its catch to Hudson's,
40% to Captain J's, and 20% to Mainstreet. The SloJoe takes 30% of its catch to Hudson's, 40% to Captain J's, and
30% to Mainstreet. One week Hudson's received 240.2 pounds of shrimp, Captain J's received 203.8 pounds, and
Mainstreet received 158 pounds. How many pounds of shrimp did each boat catch?
A)Annabelle 191 lbs, Curly Q 185 lbs, SloJoe 226 lbs
B)Annabelle 191 lbs, Curly Q 226 lbs, SloJoe 185 lbs
C)Annabelle 185 lbs, Curly Q 226 lbs, SloJoe 191 lbs
D)Annabelle 226 lbs, Curly Q 191 lbs, SloJoe 185 lbs

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck


