Deck 9: Discrete Mathematics
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/62
Play
Full screen (f)
Deck 9: Discrete Mathematics
1
Prove the following statement by mathematical induction: 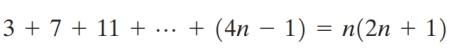
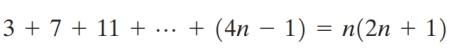
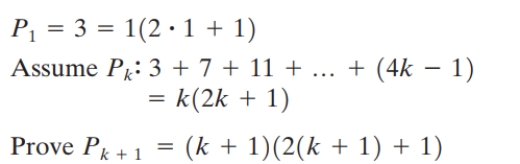
2
Determine the sixth partial sum of the geometric sequence 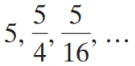
A)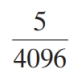
B)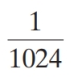
C)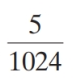
D) 6.48
E) 6.67
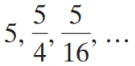
A)
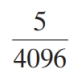
B)
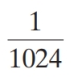
C)
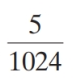
D) 6.48
E) 6.67
6.67
3
Write the statements P1, Pk , and Pk+1 for the equation 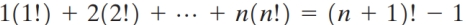 as if you were writing a proof by mathematical induction. Do not write a proof.
as if you were writing a proof by mathematical induction. Do not write a proof.
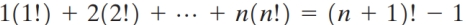 as if you were writing a proof by mathematical induction. Do not write a proof.
as if you were writing a proof by mathematical induction. Do not write a proof.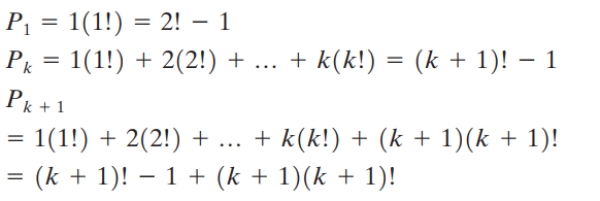
4
Find the coefficient of the 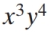 term in the expansion of
term in the expansion of 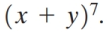
A) 3
B) 4
C)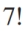
D) 35
E) 210
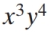 term in the expansion of
term in the expansion of 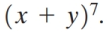
A) 3
B) 4
C)
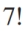
D) 35
E) 210

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
5
Find the sum of the first 12 terms of the arithmetic sequence:
28,22,16,10, ....
28,22,16,10, ....

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
6
Find the sum of the infinite series 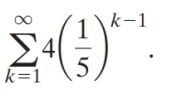
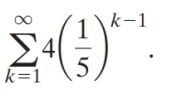

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
7
Assume that the probability that a newborn child is a female is 50% . In a family of four children, what is the probability that
(a) all the children are girls?
(b) at least two of the children are boys?
(a) all the children are girls?
(b) at least two of the children are boys?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
8
The third and fifth terms of a geometric sequence are 2 and 32, respectively. Find explicit and recursive formulas for the sequence.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
9
The sum of the squares of the first n positive odd integers is 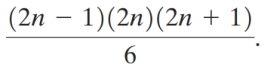
Use this expression to find the sum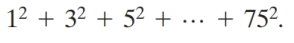
A) 5628
B) 73,150
C) 1425
D) 7,700,625
E) 5776
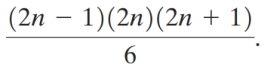
Use this expression to find the sum
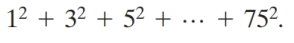
A) 5628
B) 73,150
C) 1425
D) 7,700,625
E) 5776

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
10
A fair coin is tossed five times. Find the probability of tossing exactly two tails in those five tosses.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
11


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
12
Do the following sequences converge or diverge? If they converge, state the limit.
(a)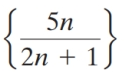
(b)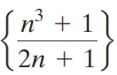
(c)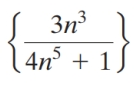
(a)
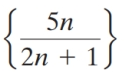
(b)
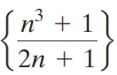
(c)
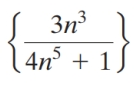

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose there is a 40% chance of rain tomorrow. If it rains, there is a 20% chance that all of the rides at an amusement park will be operating. If it doesn't rain, there is a 90% chance all of the rides will be operating. What is the probability that all of the rides will be operating tomorrow?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
14
The third and fifth terms of an arithmetic sequence are 2 and 32, respectively. Find explicit and recursive formulas for the sequence.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
15
A computer randomly selects a number from 1 through 50 . Two selections are made by the computer to create an ordered pair of numbers. How many elements are in the sample space for this experiment?
A) 2,500
B) 2,450
C) 2,000
D) 100
E) 50
A) 2,500
B) 2,450
C) 2,000
D) 100
E) 50

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
16
A computer password is 6 entries long. If the password must have 3 letters followed by 3 numbers with repetition of numbers and/or letters permitted, how many different passwords are possible?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
17
For the experiment in Problem 3, what is the probability that the computer will not select the same number in both selections?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
18
Find the fifteenth term of 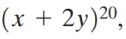 where
where 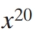 is labelled the zeroth term.
is labelled the zeroth term.
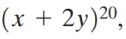 where
where 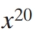 is labelled the zeroth term.
is labelled the zeroth term.
Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
19
Expand 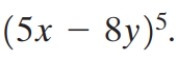
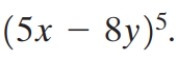

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
20
There are 85 students in a college mathematics class. Five students are chosen to work on a project together. How many different groups of five students are there in this class?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
21
Sketch a boxplot for the data in Problem 4 .


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
22
The sequence 2,6,18,54, .... is geometric.
(a) What is the common ratio of the sequence?
(b) What is a recursive rule for the n th term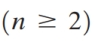 of the sequence?
of the sequence?
(a) What is the common ratio of the sequence?
(b) What is a recursive rule for the n th term
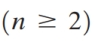 of the sequence?
of the sequence?
Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
23
Twenty-four students participated in a basketball contest. Each student took five shots. The number of baskets scored by each student is shown below. Find the mean, median, and mode for the data.



Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
24
A machine fills 16-ounce soda cans with a mean of 16.06 ounces of soda and a standard deviation of 0.03 . Approximately what percentage of the cans will actually contain less than the advertised less than the advertised 16 ounces of soda?
A) 2.5%
B) 5%
C) 10%
D) 12.5%
E) 15%
A) 2.5%
B) 5%
C) 10%
D) 12.5%
E) 15%

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
25
A hoagie consists of a roll, one type of meat, one type of cheese, and three different toppings. If there are 5 kinds of rolls, 5 kinds of meat, 4 kinds of cheese, and 9 toppings from which to choose, how many different hoagies can be built?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
26
Find the standard deviation and variance of the scores on a final exam.
65,88,83,80,78,90,92,85,74,70,95,62
65,88,83,80,78,90,92,85,74,70,95,62

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
27
The table below shows the tuition fee for one semester at a certain university.

Complete a line graph that shows this university's tuition fee trend.
B. Calculate r . Does the data show strong positive correlation?

Complete a line graph that shows this university's tuition fee trend.
B. Calculate r . Does the data show strong positive correlation?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
28
Use the formulas 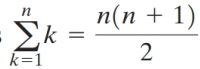 and
and
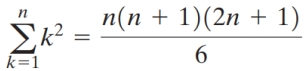 to find the sum in terms
to find the sum in terms
of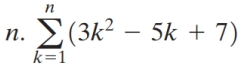
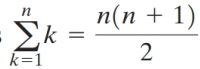 and
and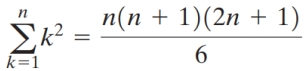 to find the sum in terms
to find the sum in termsof
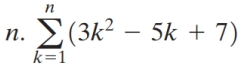

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
29
If the scores on a certain exam are normally distributed with a mean of 79 and a standard deviation of 7 , then 95% of the scores will fall in which interval?
A) [72,86]
B) [58,100]
C) [68.5,89.5]
D) [65,93]
E) [75,83]
A) [72,86]
B) [58,100]
C) [68.5,89.5]
D) [65,93]
E) [75,83]

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
30
What is the probability of obtaining exactly four heads
in eleven tosses of a fair coin?
A)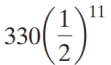
B)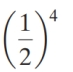
C)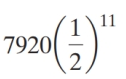
D)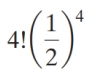
E)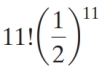
in eleven tosses of a fair coin?
A)
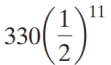
B)
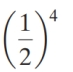
C)
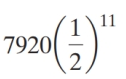
D)
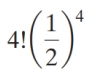
E)
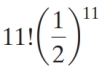

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
31
A student's grade in a particular class is determined as follows:
mean of three class exams -45%
final exam -25%
project -30%
If a student scored 85,88 , and 76 on the three exams, 90 on the final exam, and 86 on the project, what is the student's grade in the class? (Round your answer to the nearest whole number.)
mean of three class exams -45%
final exam -25%
project -30%
If a student scored 85,88 , and 76 on the three exams, 90 on the final exam, and 86 on the project, what is the student's grade in the class? (Round your answer to the nearest whole number.)

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
32
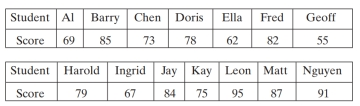
Make a histogram of the data, using interval widths of 10 points.



Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
33
Which one of the following sequences is divergent?
A)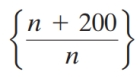
B)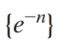
C)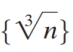
D)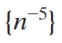
E)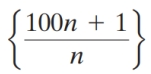
A)
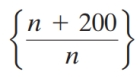
B)
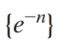
C)
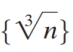
D)
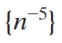
E)
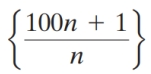

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
34
Using the binomial theorem, expand the binomial 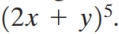
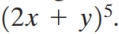

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
35


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
36
Write the series in summation notation and find the sum, assuming the suggested pattern continues.
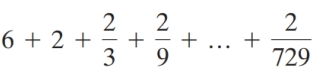
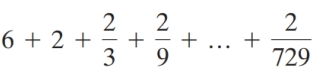

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
37
Does correlation imply causation?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
38
How many different groups of officers - president, vice-president, treasurer, and secretary - can be formed from an organization with 35 members?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
39
Find the five-number summary and the range for the data in the stemplot below.
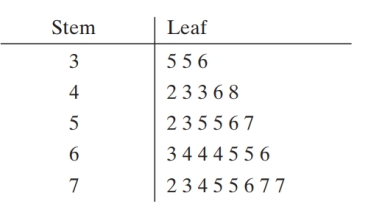


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
40
Determine whether the infinite geometric series converges. If it does converge, what is the sum?
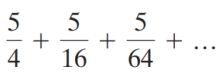
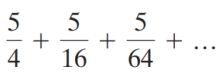

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
41
Find the mean, median, and variance. If necessary, round to the nearest hundredth.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
42
Find the probability of obtaining exactly six heads in ten tosses of a fair coin.
A)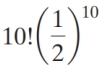
B)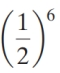
C)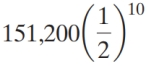
D)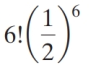
E)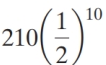
A)
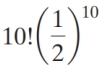
B)
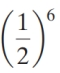
C)
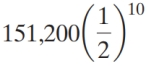
D)
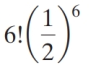
E)
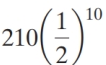

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
43
How many different groups of officers - president, vice-president, treasurer, and secretary - can be formed from an organization with 45 members?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
44
Which one of the following sequences is divergent?
A)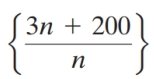
B)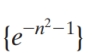
C)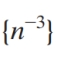
D)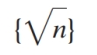
E)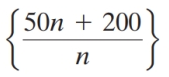
A)
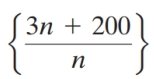
B)
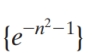
C)
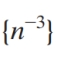
D)
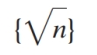
E)
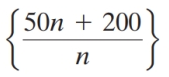

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
45
The sequence 25,21,17,13, \ldots is arithmetic.
(a) What is the common difference of the sequence?
(b) What is a recursive rule for the nth term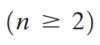 of the sequence?
of the sequence?
(a) What is the common difference of the sequence?
(b) What is a recursive rule for the nth term
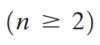 of the sequence?
of the sequence?
Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
46
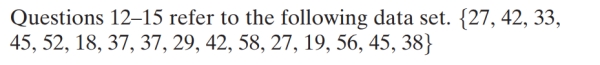
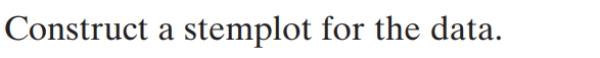

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
47
Use the formulas 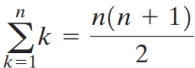 and
and
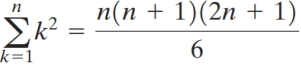
of n .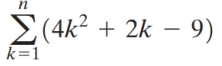
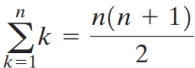 and
and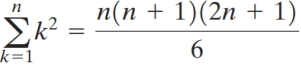
of n .
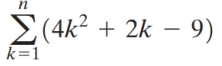

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
48
Is negative association the same as negative correlation?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
49
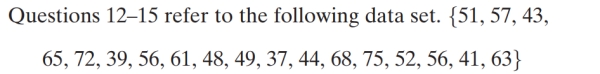
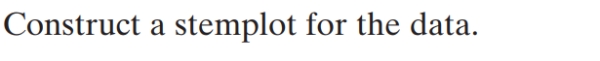

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
50
Find the mean, median, and variance. If necessary, round to the nearest hundredth.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
51
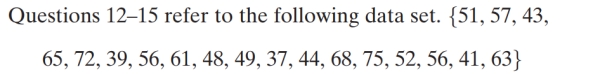


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
52
Two dice are rolled. Find the probability of rolling a sum greater than 8.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
53
Using the binomial theorem, expand the binomial 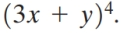
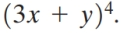

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
54
A hoagie consists of a roll, two types of meat, one type of cheese, and four different toppings. If there are 6 kinds of rolls, 7 kinds of meat, 4 kinds of cheese, and 10 toppings from which to choose, how many different hoagies can be built?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
55
Two dice are rolled. Find the probability of rolling a sum greater than 6.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
56
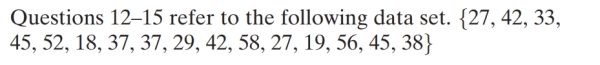


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
57
Determine whether the infinite geometric series converges. If it does converge, what is the sum?
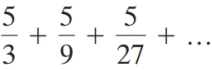
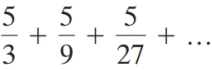

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
58
Construct a boxplot for the data.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
59
Write the series in summation notation and find the sum, assuming the suggested pattern continues.
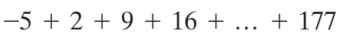
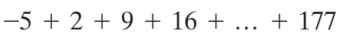

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
60
Prove the following statement by mathematical induction. 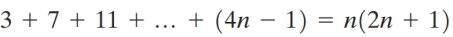
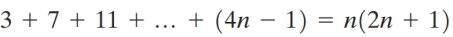

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
61
Construct a boxplot for the data.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
62
Prove the following statement by mathematical induction. 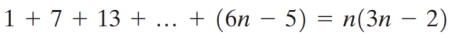
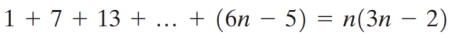

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck


