Deck 1: The Foundations: Logic and Proofs
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/200
Play
Full screen (f)
Deck 1: The Foundations: Logic and Proofs
1
What is the negation of the propositions in
Abby has more than 300 friends on facebook.
Abby has more than 300 friends on facebook.
Abby has fewer than 301 friends on facebook.
2
(a) Find a proposition with the truth table at the right.
(b) Find a proposition using only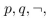 and the connective
and the connective 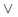 that has this truth table.
that has this truth table.
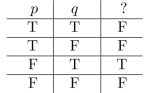
(b) Find a proposition using only
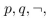 and the connective
and the connective 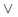 that has this truth table.
that has this truth table.
(a) 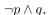
(b)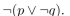
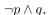
(b)
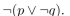
3
In questions , determine whether the proposition is TRUE or FALSE.
1 + 1 = 3 if and only if 2 + 2 = 3.
1 + 1 = 3 if and only if 2 + 2 = 3.
True
4
In questions , determine whether the proposition is TRUE or FALSE.
If it is raining, then it is raining.
If it is raining, then it is raining.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
5
Find a proposition with three variables p, q, and r that is never true.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
6
Write a proposition equivalent to 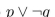 that uses only
that uses only 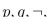 and the connective
and the connective 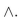
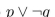 that uses only
that uses only 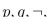 and the connective
and the connective 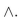

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
7
Find a proposition with three variables p, q, and r that is true when at most one of the three variables is true,
and false otherwise.
and false otherwise.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
8
What is the negation of the propositions in
A messaging package for a cell phone costs less than $20 per month.
A messaging package for a cell phone costs less than $20 per month.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
9
In questions , determine whether the proposition is TRUE or FALSE.
If 2 + 1 = 3, then 2 = 3 − 1.
If 2 + 1 = 3, then 2 = 3 − 1.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
10
Determine whether 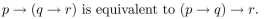
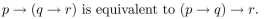

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
11
Find a proposition with three variables p, q, and r that is true when p and r are true and q is false, and false
otherwise.
otherwise.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
12
Determine whether 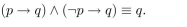
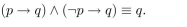

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
13
Write a proposition equivalent to 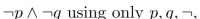 and the connective
and the connective 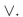
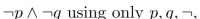 and the connective
and the connective 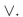

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
14
Determine whether 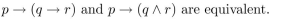
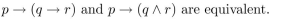

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
15
In questions , determine whether the proposition is TRUE or FALSE.
If 1 < 0, then 3 = 4.
If 1 < 0, then 3 = 4.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
16
In questions , determine whether the proposition is TRUE or FALSE.
If 1 + 1 = 2 or 1 + 1 = 3, then 2 + 2 = 3 and 2 + 2 = 4.
If 1 + 1 = 2 or 1 + 1 = 3, then 2 + 2 = 3 and 2 + 2 = 4.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
17
Write the truth table for the proposition 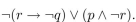
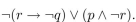

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
18
What is the negation of the propositions in
4.5 + 2.5 = 6
4.5 + 2.5 = 6

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
19
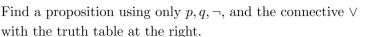
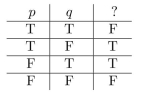

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
20
Prove that the proposition "if it is not hot, then it is hot" is equivalent to "it is hot".

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
21
Write a proposition equivalent to 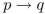 using only
using only 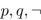 , and the connective
, and the connective 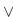 .
.
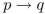 using only
using only 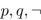 , and the connective
, and the connective 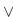 .
.
Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
22
write the statement in the form "If . . . , then . . . ."
The team wins if the quarterback can pass.
The team wins if the quarterback can pass.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
23
write the statement in the form "If . . . , then . . . ."
It is hot whenever it is sunny.
It is hot whenever it is sunny.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
24
Write the contrapositive, converse, and inverse of the following: You sleep late if it is Saturday.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
25
Determine whether the following two propositions are logically equivalent: 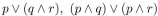
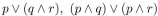

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
26
Write a proposition equivalent to 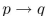 using only
using only 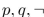 , and the connective
, and the connective 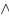 .
.
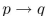 using only
using only 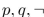 , and the connective
, and the connective 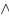 .
.
Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
27
Prove that 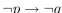 and its inverse are not logically equivalent.
and its inverse are not logically equivalent.
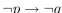 and its inverse are not logically equivalent.
and its inverse are not logically equivalent.
Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
28
write the negation of the statement. (Don't write "It is not true that . . . .")
It is Thursday and it is cold.
It is Thursday and it is cold.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
29
Prove that 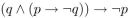 is a tautology using propositional equivalence and the laws of logic.
is a tautology using propositional equivalence and the laws of logic.
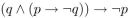 is a tautology using propositional equivalence and the laws of logic.
is a tautology using propositional equivalence and the laws of logic.
Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
30
write the statement in the form "If . . . , then . . . ."
You need to be registered in order to check out library books.
You need to be registered in order to check out library books.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
31
Write the contrapositive, converse, and inverse of the following: If you try hard, then you will win.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
32
write the statement in the form "If . . . , then . . . ."
To get a good grade it is necessary that you study.
To get a good grade it is necessary that you study.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
33
write the statement in the form "If . . . , then . . . ."
Studying is sufficient for passing.
Studying is sufficient for passing.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
34
write the negation of the statement. (Don't write "It is not true that . . . .")
I will go to the play or read a book, but not both.
I will go to the play or read a book, but not both.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
35
Determine whether this proposition is a tautology: 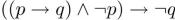
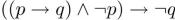

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
36
Prove that 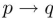 and its converse are not logically equivalent.
and its converse are not logically equivalent.
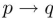 and its converse are not logically equivalent.
and its converse are not logically equivalent.
Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
37
write the statement in the form "If . . . , then . . . ."
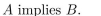
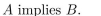

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
38
write the statement in the form "If . . . , then . . . ."
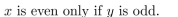
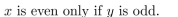

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
39
Determine whether the following two propositions are logically equivalent: 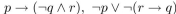
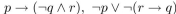

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
40
Determine whether this proposition is a tautology: 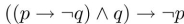
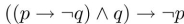

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
41
Using c for "it is cold", r for "it is rainy", and w for "it is windy", write "It is rainy only if it is windy and
cold" in symbols.
cold" in symbols.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
42
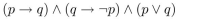

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
43
On the island of knights and knaves you encounter two people, A and
B. Person A says "B is a knave."
Person B says "At least one of us is a knight." Determine whether each person is a knight or a knave.
Exercises 51-53 relate to inhabitants of an island on which there are three kinds of people: knights who always
tell the truth, knaves who always lie, and spies who can either tell the truth or lie. You encounter three people,
A, B, and
C. You know one of the three people is a knight, one is a knave, and one is a spy. Each of the three
B. Person A says "B is a knave."
Person B says "At least one of us is a knight." Determine whether each person is a knight or a knave.
Exercises 51-53 relate to inhabitants of an island on which there are three kinds of people: knights who always
tell the truth, knaves who always lie, and spies who can either tell the truth or lie. You encounter three people,
A, B, and
C. You know one of the three people is a knight, one is a knave, and one is a spy. Each of the three

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
44
On the island of knights and knaves you encounter two people, A and
B. Person A says "B is a knave."
Person B says "We are both knights." Determine whether each person is a knight or a knave.
B. Person A says "B is a knave."
Person B says "We are both knights." Determine whether each person is a knight or a knave.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
45
Explain why the negation of "Al and Bill are absent" is not "Al and Bill are present".

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
46
people knows the type of person each of the other two is. For each of these situations, if possible, determine
whether there is a unique solution, list all possible solutions or state that there are no solutions.
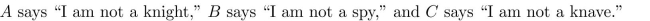
whether there is a unique solution, list all possible solutions or state that there are no solutions.
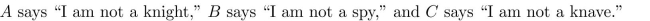

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
47
people knows the type of person each of the other two is. For each of these situations, if possible, determine
whether there is a unique solution, list all possible solutions or state that there are no solutions.
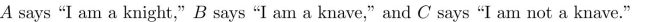
whether there is a unique solution, list all possible solutions or state that there are no solutions.
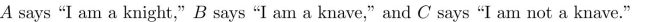

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
48
Construct a combinatorial circuit using inverters, OR gates, and AND gates, that produces the outputs in from input bits p, q and r.
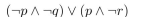
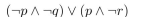

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
49
Using c for "it is cold" and r for "it is rainy", write "It is rainy if it is not cold" in symbols.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
50
people knows the type of person each of the other two is. For each of these situations, if possible, determine
whether there is a unique solution, list all possible solutions or state that there are no solutions.
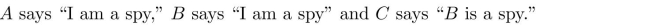
whether there is a unique solution, list all possible solutions or state that there are no solutions.
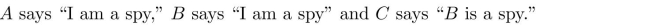

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
51
Using c for "it is cold" and w for "it is windy", write "To be windy it is necessary that it be cold" in symbols.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
52
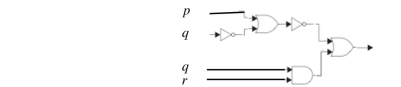

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
53
Translate the given statement into propositional logic using the propositions provided: On certain highways
in the Washington, DC metro area you are allowed to travel on high occupancy lanes during rush hour only
if there are at least three passengers in the vehicle. Express your answer in terms of r:"You are traveling
during rush hour." t:"You are riding in a car with at least three passengers." and h:"You can travel on a high
occupancy lane."
in the Washington, DC metro area you are allowed to travel on high occupancy lanes during rush hour only
if there are at least three passengers in the vehicle. Express your answer in terms of r:"You are traveling
during rush hour." t:"You are riding in a car with at least three passengers." and h:"You can travel on a high
occupancy lane."

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
54
A set of propositions is consistent if there is an assignment of truth values to each of the variables in the
propositions that makes each proposition true. Is the following set of propositions consistent?
The system is in multiuser state if and only if it is operating normally.
If the system is operating normally, the kernel is functioning.
The kernel is not functioning or the system is in interrupt mode.
If the system is not in multiuser state, then it is in interrupt mode.
The system is in interrupt mode.
propositions that makes each proposition true. Is the following set of propositions consistent?
The system is in multiuser state if and only if it is operating normally.
If the system is operating normally, the kernel is functioning.
The kernel is not functioning or the system is in interrupt mode.
If the system is not in multiuser state, then it is in interrupt mode.
The system is in interrupt mode.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
55
suppose that 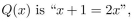 where x is a real number. Find the truth value of the statement.
where x is a real number. Find the truth value of the statement.
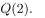
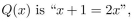 where x is a real number. Find the truth value of the statement.
where x is a real number. Find the truth value of the statement.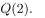

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
56
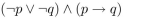

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
57
Construct a combinatorial circuit using inverters, OR gates, and AND gates, that produces the outputs in from input bits p, q and r.
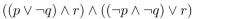 Determine whether the compound propositions in 58-59 are satisfiable.
Determine whether the compound propositions in 58-59 are satisfiable.
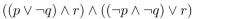 Determine whether the compound propositions in 58-59 are satisfiable.
Determine whether the compound propositions in 58-59 are satisfiable.
Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
58
write the negation of the statement. (Don't write "It is not true that . . . .")
If it is rainy, then we go to the movies.
If it is rainy, then we go to the movies.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
59
Find the output of the combinatorial circuits in 54-55.
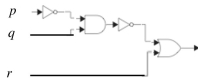


Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
60
Using c for "it is cold" and d for "it is dry", write "It is neither cold nor dry" in symbols.

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
61
P(x, y) means "x and y are real numbers such that 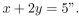 Determine whether the statement
Determine whether the statement
is true.
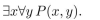 In 73-75 P(m, n) means
In 73-75 P(m, n) means 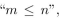 where the universe of discourse for m and n is the set of nonnegative
where the universe of discourse for m and n is the set of nonnegative
integers. What is the truth value of the statement?
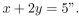 Determine whether the statement
Determine whether the statementis true.
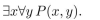 In 73-75 P(m, n) means
In 73-75 P(m, n) means 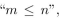 where the universe of discourse for m and n is the set of nonnegative
where the universe of discourse for m and n is the set of nonnegativeintegers. What is the truth value of the statement?

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
62
P(m, n) means
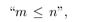
where the universe of discourse for m and n is the set of nonnegative
integers. What is the truth value of the statement?
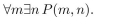
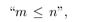
where the universe of discourse for m and n is the set of nonnegative
integers. What is the truth value of the statement?
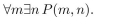

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
63
suppose that 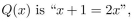 where x is a real number. Find the truth value of the statement.
where x is a real number. Find the truth value of the statement.
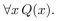
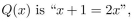 where x is a real number. Find the truth value of the statement.
where x is a real number. Find the truth value of the statement.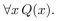

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
64
P(x, y) means
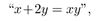 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.
P(0, 0).
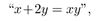 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.P(0, 0).

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
65
P(x, y) is a predicate and the universe for the variables x and y is {1, 2, 3}. Suppose
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
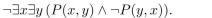
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
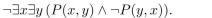

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
66
P(x, y) is a predicate and the universe for the variables x and y is {1, 2, 3}. Suppose
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
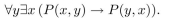
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
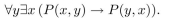

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
67
P(x, y) means
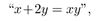 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.
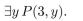
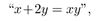 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.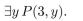

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
68
P(m, n) means
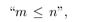
where the universe of discourse for m and n is the set of nonnegative
integers. What is the truth value of the statement?
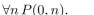
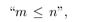
where the universe of discourse for m and n is the set of nonnegative
integers. What is the truth value of the statement?
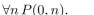

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
69
P(x, y) is a predicate and the universe for the variables x and y is {1, 2, 3}. Suppose
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
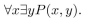
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
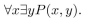

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
70
P(x, y) means
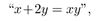 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.
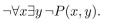
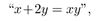 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.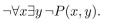

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
71
suppose that 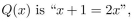 where x is a real number. Find the truth value of the statement.
where x is a real number. Find the truth value of the statement.
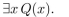 In 63-70 P(x, y) means
In 63-70 P(x, y) means 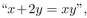 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.
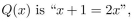 where x is a real number. Find the truth value of the statement.
where x is a real number. Find the truth value of the statement.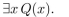 In 63-70 P(x, y) means
In 63-70 P(x, y) means 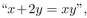 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.
Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
72
P(x, y) means
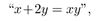 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.
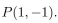
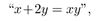 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.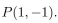

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
73
P(x, y) means
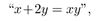 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.
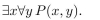
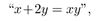 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.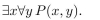

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
74
P(x, y) means
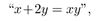 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.
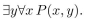
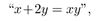 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.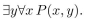

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
75
P(x, y) is a predicate and the universe for the variables x and y is {1, 2, 3}. Suppose
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
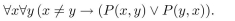
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
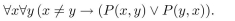

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
76
P(x, y) is a predicate and the universe for the variables x and y is {1, 2, 3}. Suppose
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
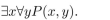
P(1, 3), P(2, 1), P(2, 2), P(2, 3), P(3, 1), P(3, 2) are true, and P(x, y) is false otherwise. Determine whether
the following statements are true.
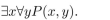

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
77
P(x, y) means "x and y are real numbers such that 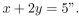 Determine whether the statement
Determine whether the statement
is true.
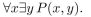
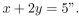 Determine whether the statement
Determine whether the statementis true.
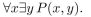

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
78
P(m, n) means
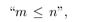
where the universe of discourse for m and n is the set of nonnegative
integers. What is the truth value of the statement?
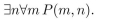
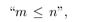
where the universe of discourse for m and n is the set of nonnegative
integers. What is the truth value of the statement?
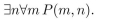

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
79
P(x, y) means
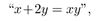 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.
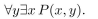
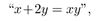 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.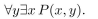

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck
80
P(x, y) means
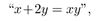 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.
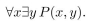
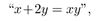 where x and y are integers. Determine the truth value of the statement.
where x and y are integers. Determine the truth value of the statement.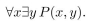

Unlock Deck
Unlock for access to all 200 flashcards in this deck.
Unlock Deck
k this deck


