Deck 7: Systems of Equations and Matrices
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/196
Play
Full screen (f)
Deck 7: Systems of Equations and Matrices
1
The following system does not have a unique solution. Solve the system.
A)x = - 8 , y & = 1 , z = - 1
B) infinitely many solutions of the form
C) infinitely many solutions of the form
D) inconsistent system, no solution
A)x = - 8 , y & = 1 , z = - 1
B) infinitely many solutions of the form
C) infinitely many solutions of the form
D) inconsistent system, no solution
B
2
The following system does not have a unique solution. Solve the system.
A) infinitely many solutions of the form
B) inconsistent system, no solution
C)
D) infinitely many solutions of the form
A) infinitely many solutions of the form
B) inconsistent system, no solution
C)
D) infinitely many solutions of the form
A
3
The following system does not have a unique solution. Solve the system.
B) infinitely many solutions of the form
C) inconsistent system, no solution
D)
B) infinitely many solutions of the form
C) inconsistent system, no solution
D)
B
4
Linda invests $25,000 for one year. Part is invested at 5%, another part at 6%, and the rest at 8%. The total income from all 3 investments is $1600. The total income from the 5% and 6% investments is equal to the income
From the 8% investment. Find the amount invested at each rate.
A) $10,000 at 5%, $10,000 at 6%, $5000 at 8%
B) $5000 at 5%, $10,000 at 6%, $10,000 at 8%
C) $10,000 at 5%, $5000 at 6%, $10,000 at 8%
D) $8000 at 5%, $10,000 at 6%, $7000 at 8%
From the 8% investment. Find the amount invested at each rate.
A) $10,000 at 5%, $10,000 at 6%, $5000 at 8%
B) $5000 at 5%, $10,000 at 6%, $10,000 at 8%
C) $10,000 at 5%, $5000 at 6%, $10,000 at 8%
D) $8000 at 5%, $10,000 at 6%, $7000 at 8%

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
5
A company manufactures three types of cable. Cable A requires 3 black wires, 3 white wires, and 2 red wires. Cable B requires 1 black, 2 white, and 1 red. Cable C requires 2 black, 1 white, and 2 red. If 100 black wires, 110
White wires, and 90 red wires are required to complete an order, how many of each type of cable are in the
Order?
A) 20 cable A, 30 cable B, 10 cable C
B) 10 cable A, 30 cable B, 20 cable C
C) 10 cable A, 103 cable B, 20 cable C
D) 10 cable A, 30 cable B, 93 cable C
White wires, and 90 red wires are required to complete an order, how many of each type of cable are in the
Order?
A) 20 cable A, 30 cable B, 10 cable C
B) 10 cable A, 30 cable B, 20 cable C
C) 10 cable A, 103 cable B, 20 cable C
D) 10 cable A, 30 cable B, 93 cable C

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
6
A) x=-3, y=0, z=4
B) x=3, y=0, z=-4
C) x=0, y=6, z=-1
D) x=0, y=-6, z=1

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
7
A) x=5, y=4, z=3
B) No solution
C) x=3, y=4, z=5
D) x=3, y=5, z=4

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
8
A $100,000 trust is to be invested in bonds paying 9%, CDs paying 7%, and mortgages paying 10%. The sum of the bond and CD investment must equal the mortgage investment. To earn an $9100 annual income from the
Investments, how much should the bank invest in bonds?
A) $20,000
B) $30,000
C) $28,000
D) $50,000
Investments, how much should the bank invest in bonds?
A) $20,000
B) $30,000
C) $28,000
D) $50,000

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
9
A) x=-1, y=2, z=-3
B) x=1, y=2, z=3
C) x=3, y=-2, z=5
D) x=0, y=4, z=2

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
10
A) x=2, y=7, z=-1
B) x=2, y=-7, z=1
C) x=2, y=7, z=1
D) x=2, y=-7, z=-1

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
11
A) x=1, y=-1, z=1
B) x=-1, y=1, z=1
C) x=0, y=0, z=1
D) x=0, y=1, z=0

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
12
The following system does not have a unique solution. Solve the system.
A) infinitely many solutions of the form
B) infinitely many solutions of the form
C) infinitely many solutions of the form
D) infinitely many solutions of the form
A) infinitely many solutions of the form
B) infinitely many solutions of the form
C) infinitely many solutions of the form
D) infinitely many solutions of the form

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
13
The sum of a student's three scores is 230. If the first is 19 points more than the second, and the sum of the first two is 23 more than twice the third, then what was the first score?
A) 50
B) 90
C) 69
D) 71
A) 50
B) 90
C) 69
D) 71

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
14
The following system does not have a unique solution. Solve the system.
A)
B)
C) inconsistent system, no solution
D)
A)
B)
C) inconsistent system, no solution
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
15
A) x=-5, y=8, z=13
B) x=5, y=-8, z=-13
C) x=-5, y=-8, z=13
D) x=5, y=8, z=-13

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
16
The following system does not have a unique solution. Solve the system.
A)
B)
C) inconsistent system, no solution
D)
A)
B)
C) inconsistent system, no solution
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
17
Some people must eat a low-sodium diet with no more than 2000 mg of sodium per day. By eating 1 cracker, 1 pretzel, and 1 cookie, a person would ingest 149 mg of sodium. If a person ate 8 pretzels and 8 cookies, he or she
Would ingest 936 mg of sodium. By eating 6 crackers and 7 pretzels, a person would take in 535 mg of sodium.
Which of the following statements is true?
A) A cracker contains more sodium than a cookie.
B) A cookie contains 71 mg of sodium.
C) A cracker contains 30 mg of sodium.
D) A pretzel contains 49 mg of sodium.
Would ingest 936 mg of sodium. By eating 6 crackers and 7 pretzels, a person would take in 535 mg of sodium.
Which of the following statements is true?
A) A cracker contains more sodium than a cookie.
B) A cookie contains 71 mg of sodium.
C) A cracker contains 30 mg of sodium.
D) A pretzel contains 49 mg of sodium.

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
18
A) x=-2, y=-1, z=9
B) x=2, y=-1, z=-9
C) x=-2, y=-1, z=-9
D) x=2, y=-1, z=9

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
19
A) x=4, y=1, z=2
B) x=1, y=2, z=4
C) x=1, y=4, z=2
D) x=4, y=2, z=1

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
20
A) x=0, y=8, z=0
B) x=0, y=-8, z=-8
C) x=8, y=8, z=0
D) x=-8, y=0, z=0

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
21
The matrix associated with the solution to a system of linear equations in x, y, and z is given. Write the solution to the
system, if it exists.
A)
B)
C)
D)
system, if it exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
22
Write the augmented matrix associated with the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
23
A psychologist studying the effects of good nutrition on the behavior of rabbits feeds one group a combination of three foods, I, II, and III. Each of these foods contains three additives, A, B, and C, that are used in the study.
The table below gives the percent of each additive that is present in each food. If the diet being used requires
19)1 g per day of A, 8.94 g of B, and 14.02 g of C, find the number of grams of food II that should be used each
Day) Let z represent the number of grams of food III.
A)
B)
C)
D)
The table below gives the percent of each additive that is present in each food. If the diet being used requires
19)1 g per day of A, 8.94 g of B, and 14.02 g of C, find the number of grams of food II that should be used each
Day) Let z represent the number of grams of food III.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
24
Write the augmented matrix associated with the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
25
A bank gives three loans totaling $330,000 to a development company for the purchase of three business properties. The largest loan is $38,000 more than the sum of the other two. Find the amount of the largest loan.
A) $192,000
B) $195,000
C) $184,000
D) $180,000
A) $192,000
B) $195,000
C) $184,000
D) $180,000

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
26
A bakery sells three types of cakes. The table below gives the number of cups of flour, cups of sugar, and eggs needed to produce each type of cake. 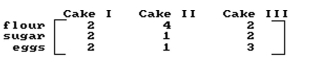
To fill its orders for cakes, the bakery used 72 cups of flour, 48 cups of sugar, and 51 eggs. How many cakes of each
Type were made?
A) 19 cake I, 8 cake II, 3 cake III
B) 41 cake I, 8 cake II, 12 cake III
C) 17 cake I, 8 cake II, 3 cake III
D) 3 cake I, 8 cake II, 17 cake III
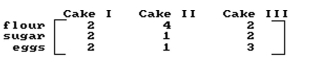
To fill its orders for cakes, the bakery used 72 cups of flour, 48 cups of sugar, and 51 eggs. How many cakes of each
Type were made?
A) 19 cake I, 8 cake II, 3 cake III
B) 41 cake I, 8 cake II, 12 cake III
C) 17 cake I, 8 cake II, 3 cake III
D) 3 cake I, 8 cake II, 17 cake III

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
27
Write the augmented matrix associated with the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
28
A trust account manager has $400,000 to be invested in three different accounts. The accounts pay 5%, 6%, and 10%, and the goal is to earn $32,000. Assuming that x dollars are invested at 5%, y dollars are invested at 6%,
And z dollars are invested at 8%, what limits must there be on z so that all investment values are non-negative? A)
B)
C)
D)
And z dollars are invested at 8%, what limits must there be on z so that all investment values are non-negative? A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
29
A trust account manager has $300,000 to be invested in three different accounts. The accounts pay 5%, 6%, and 8%, and the goal is to earn $18,000. Assuming that x dollars are invested at 5%, y dollars are invested at 6%, and
Z dollars are invested at 8%, find x in terms of z. A)
B)
C)
D)
Z dollars are invested at 8%, find x in terms of z. A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
30
A basketball fieldhouse seats 15,000. Courtside seats sell for $8, endzone for $7, and balcony for $5. A full house earns $88,000 in ticket revenue. If half the courtside and balcony seats and all the endzone seats are sold, the
Total ticket revenue is $51,000. How many of each type of seat are there?
A) 4000 courtside, 3000 endzone, 8000 balcony
B) 4000 courtside, 1500 endzone, 9500 balcony
C) 3200 courtside, 1800 endzone, 10,000 balcony
D) 3000 courtside, 2000 endzone, 10,000 balcony
Total ticket revenue is $51,000. How many of each type of seat are there?
A) 4000 courtside, 3000 endzone, 8000 balcony
B) 4000 courtside, 1500 endzone, 9500 balcony
C) 3200 courtside, 1800 endzone, 10,000 balcony
D) 3000 courtside, 2000 endzone, 10,000 balcony

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
31
Write the augmented matrix associated with the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
32
The Hoffman Trucking Company has an order for three products, A, B, and C, for delivery. The table below gives the volume in cubic feet, the weight in pounds, and the value for insurance in dollars for a unit of each of
The products. If one of the company's trucks can carry 38,000 cubic feet and 57,100 pounds, and is insured to
Carry $29,750, how many units of product A can be carried on the truck? Assume that z represents the number
Of units of product C.
A)
B)
C)
D) There is no solution.
The products. If one of the company's trucks can carry 38,000 cubic feet and 57,100 pounds, and is insured to
Carry $29,750, how many units of product A can be carried on the truck? Assume that z represents the number
Of units of product C.
A)
B)
C)
D) There is no solution.

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
33
The matrix associated with the solution to a system of linear equations in x, y, and z is given. Write the solution to the
system, if it exists.
A)
B)
C)
D)
system, if it exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
34
A young woman wins $150,000 and buys 5 new cars. She chooses from cars that are priced at $40,000, $30,000, and $25,000 and spends all of the money. How many $25,000 cars did she buy?
A) 0 or 2
B) 0, 1, 2, or 3
C) 6
D) 0
A) 0 or 2
B) 0, 1, 2, or 3
C) 6
D) 0

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
35
Write the augmented matrix associated with the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
36
A company offers three mutual fund plans for its employees. Plan I consists of 2 blocks of common stocks, 3 municipal bonds, and 4 blocks of preferred stock. Plan II consists of 2 blocks of common stocks, 2 municipal
Bonds, and 1 block of preferred stock. Plan III consists of 4 blocks of common stocks, 5 municipal bonds, and 5
Blocks of preferred stock. An employee combined these plans so that he has 22 blocks of common stock, 27
Municipal bonds, and 26 blocks of preferred stock. How many units of plan III might he have?
A) 0, 1, 2, 3, 4, or 5
B) 3, 4, 5, or 6
C) 0, 1, 2, 3, 4, 5, or 6
D) 3, 4, or 5
Bonds, and 1 block of preferred stock. Plan III consists of 4 blocks of common stocks, 5 municipal bonds, and 5
Blocks of preferred stock. An employee combined these plans so that he has 22 blocks of common stock, 27
Municipal bonds, and 26 blocks of preferred stock. How many units of plan III might he have?
A) 0, 1, 2, 3, 4, or 5
B) 3, 4, 5, or 6
C) 0, 1, 2, 3, 4, 5, or 6
D) 3, 4, or 5

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
37
A man has a total of $110,000 invested in three rental properties. One property earns 7.5% per year on its investment, the second earns 9%, and the third earns 10%. The three properties earn a total of $9600 per year.
What is the largest amount that could be invested at 7.5%?
A) $56,000
B) $110,000
C) $50,000
D) $54,000
What is the largest amount that could be invested at 7.5%?
A) $56,000
B) $110,000
C) $50,000
D) $54,000

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
38
A trust account manager has $500,000 to be invested in three different accounts. The accounts pay 5%, 6%, and 8%, and the goal is to earn $34,000. Assuming that x dollars are invested at 5%, y dollars are invested at 6%, and
Z dollars are invested at 8%, find y in terms of z. A)
B)
C)
D)
Z dollars are invested at 8%, find y in terms of z. A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
39
The matrix associated with the solution to a system of linear equations in x, y, and z is given. Write the solution to the
system, if it exists.
A)
B)
C)
D)
system, if it exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
40
The matrix associated with the solution to a system of linear equations in x, y, and z is given. Write the solution to the
system, if it exists.
A)
B)
C)
D)
system, if it exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
41
A) x=1, y=-1, z=3, w=-2
B) x=-3, y=-3, z=1, w=-2
C) x=3, y=-3, z=1, w=-1
D) x=3, y=-6, z=-1, w=-1

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
42
A) infinitely many solutions of the form
B) infinitely many solutions of the form
C) infinitely many solutions of the form
D) infinitely many solutions of the form

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
43
Find the solution or solutions, if any exist, to the system.
A) infinitely many solutions of the form
B)
C) infinitely many solutions of the form
D) inconsistent system, no solution
A) infinitely many solutions of the form
B)
C) infinitely many solutions of the form
D) inconsistent system, no solution

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
44
The matrix associated with the solution to a system of linear equations in x, y, and z is given. Write the solution to the
system, if it exists.
A)
B)
C)
D)
system, if it exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
45
The matrix associated with the solution to a system of linear equations in x, y, and z is given. Write the solution to the
system, if it exists.
A)
B)
C)
D)
system, if it exists.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
46
Find the solution or solutions, if any exist, to the system.
A) infinitely many solutions of the form
B) infinitely many solutions of the form
C) infinitely many solutions of the form
D) infinitely many solutions of the form
A) infinitely many solutions of the form
B) infinitely many solutions of the form
C) infinitely many solutions of the form
D) infinitely many solutions of the form

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
47
A) infinitely many solutions of the form
B) infinitely many solutions of the form
C)
D) infinitely many solutions of the form

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
48
A) x=1, y=-4, z=4, w=-1
B) x=6, y=-24, z=16, w=-6
C) x=1, y=-24, z=8, w=-2
D) x=1, y=-4, z=16, w=-1

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
49
A)
B) infinitely many solutions of the form
C) inconsistent system, no solution
D) infinitely many solutions of the form

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
50
Find the solution or solutions, if any exist, to the system.
A)
B)
C) inconsistent system, no solution
D)
A)
B)
C) inconsistent system, no solution
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
51
A) x=1, y=4, z=2
B) x=4, y=1, z=2
C) x=4, y=2, z=1
D) x=1, y=2, z=4

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
52
Find the solution or solutions, if any exist, to the system.
A) x = 0 , y = 1 , z = - 3
B) infinitely many solutions of the form
C)
D) inconsistent system, no solution
A) x = 0 , y = 1 , z = - 3
B) infinitely many solutions of the form
C)
D) inconsistent system, no solution

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
53
A) infinitely many solutions of the form
B) infinitely many solutions of the form
C) infinitely many solutions of the form
D) infinitely many solutions of the form

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
54
A) x=-2, y=4, z=3, w=-5
B) x=4, y=-2, z=-7, w=-4
C) x=3, y=0, z=-1, w=0
D) x=4, y=-2, z=1, w=-4

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
55
Find the solution or solutions, if any exist, to the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
56
A) x=3, y=0, z=-4
B) x=0, y=-6, z=1
C) x=0, y=6, z=-1
D) x=-3, y=0, z=4

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
57
A) x=-2, y=-1, z=-9
B) x=2, y=-1, z=9
C) x=-2, y=-1, z=9
D) x=2, y=-1, z=-9

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
58
Find the solution or solutions, if any exist, to the system.
A) infinitely many solutions of the form
B) infinitely many solutions of the form
C) infinitely many solutions of the form
D) infinitely many solutions of the form
A) infinitely many solutions of the form
B) infinitely many solutions of the form
C) infinitely many solutions of the form
D) infinitely many solutions of the form

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
59
A) x=5, y=3, z=-1, w=-1
B) x=-10, y=0, z=-2, w=1
C) x=0, y=-5, z=1, w=5
D) x=-5, y=1, z=-1, w=0

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
60
A) x=4, y=-1, z=5, w=-4
B) x=-1, y=3, z=6, w=1
C) x=4, y=-2, z=0, w=4
D) x=-4, y=-5, z=10, w=4

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
61
Find the indicated sum or difference, if it is defined.
A)
B) not defined
C)
D)
A)
B) not defined
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
62
Find the indicated matrix.
Let . Find .
A)
B)
C)
D)
Let . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
63
In an analysis of traffic, a certain city estimates the traffic flow as illustrated in the figure below, where the arrows indicate the flow of traffic. If x1 represents the number of cars traveling from intersection A to intersection B, x2 represents the number of cars traveling from intersection B to intersection C , and so on, we car formulate equations based on the principle that the number of vehicles entering the intersection equals the numt leaving it. Formulate an equation for the traffic at each of the four intersections.
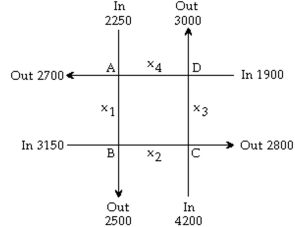
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
64
Find the indicated sum or difference, if it is defined.
A)
B) not defined
C)
D)
A)
B) not defined
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
65
Some people must eat a low-sodium diet with no more than 2000 mg of sodium per day. By eating 1 cracker, 1 pretzel, and 1 cookie, a person would ingest 149 mg of sodium. If a person ate 8 pretzels and 8 cookies, he or she
Would ingest 936 mg of sodium. By eating 6 crackers and 7 pretzels, a person would take in 535 mg of sodium.
Which of the following statements is true?
A) A pretzel contains 49 mg of sodium.
B) A cracker contains more sodium than a cookie
C) A cracker contains 30 mg of sodium.
D) A cookie contains 71 mg of sodium.
Would ingest 936 mg of sodium. By eating 6 crackers and 7 pretzels, a person would take in 535 mg of sodium.
Which of the following statements is true?
A) A pretzel contains 49 mg of sodium.
B) A cracker contains more sodium than a cookie
C) A cracker contains 30 mg of sodium.
D) A cookie contains 71 mg of sodium.

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
66
The sum of a student's three scores is 224. If the first is 13 points more than the second, and the sum of the first two is 29 more than twice the third, then what was the first score?
A) 65
B) 86
C) 52
D) 73
A) 65
B) 86
C) 52
D) 73

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
67
Find the solution or solutions, if any exist, to the system.
A man has invested in three rental properties. One property earns per year on the investment, a second earns , and the third earns . The annual earnings from the the properties total . Write a system of two equations to represent the problem with , and representing the , and investments, respectively.
A)
B)
C)
D)
A man has invested in three rental properties. One property earns per year on the investment, a second earns , and the third earns . The annual earnings from the the properties total . Write a system of two equations to represent the problem with , and representing the , and investments, respectively.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
68
Find the indicated sum or difference, if it is defined.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
69
A basketball fieldhouse seats 15,000. Courtside seats sell for $8, endzone for $7, and balcony for $5. A full house earns $88,000 in ticket revenue. If half the courtside and balcony seats and all the endzone seats are sold, the
Total ticket revenue is $51,000. How many of each type of seat are there?
A) 4000 courtside, 1500 endzone, 9500 balcony
B) 4000 courtside, 3000 endzone, 8000 balcony
C) 3000 courtside, 2000 endzone, 10,000 balcony
D) 3200 courtside, 1800 endzone, 10,000 balcony
Total ticket revenue is $51,000. How many of each type of seat are there?
A) 4000 courtside, 1500 endzone, 9500 balcony
B) 4000 courtside, 3000 endzone, 8000 balcony
C) 3000 courtside, 2000 endzone, 10,000 balcony
D) 3200 courtside, 1800 endzone, 10,000 balcony

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
70
Find the indicated sum or difference, if it is defined.
A)
B)
C)
D) not defined
A)
B)
C)
D) not defined

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
71
Find the indicated matrix.
Let . Find -2B.
A)
B)
C)
D)
Let . Find -2B.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
72
Find the indicated sum or difference, if it is defined.
A)
B)
C) not defined
D)
A)
B)
C) not defined
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
73
A young woman wins $150,000 and buys 5 new cars. She chooses from cars that are priced at $40,000, $30,000, and $25,000 and spends all of the money. How many $25,000 cars did she buy?
A) 0, 1, 2, or 3
B) 0
C) 6
D) 0 or 2
A) 0, 1, 2, or 3
B) 0
C) 6
D) 0 or 2

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
74
Find the indicated sum or difference, if it is defined.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
75
Linda invests $25,000 for one year. Part is invested at 5%, another part at 6%, and the rest at 8%. The total income from all 3 investments is $1600. The total income from the 5% and 6% investments is equal to the income
From the 8% investment. Find the amount invested at each rate.
A) $10,000 at 5%, $10,000 at 6%, $5000 at 8%
B) $10,000 at 5%, $5000 at 6%, $10,000 at 8%
C) $8000 at 5%, $10,000 at 6%, $7000 at 8%
D) $5000 at 5%, $10,000 at 6%, $10,000 at 8%
From the 8% investment. Find the amount invested at each rate.
A) $10,000 at 5%, $10,000 at 6%, $5000 at 8%
B) $10,000 at 5%, $5000 at 6%, $10,000 at 8%
C) $8000 at 5%, $10,000 at 6%, $7000 at 8%
D) $5000 at 5%, $10,000 at 6%, $10,000 at 8%

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
76
Find the indicated sum or difference, if it is defined.
Compute the sum of and .
A)
В)
C)
D)
Compute the sum of and .
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
77
Find the indicated matrix.
Let . Find .
A)
B)
C)
D)
Let . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
78
Find the indicated sum or difference, if it is defined.
Compute the difference if and .
A)
B)
C)
D)
Compute the difference if and .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
79
Find the solution or solutions, if any exist, to the system.
A) infinitely many solutions of the form
B) inconsistent system, no solution
C)
D) infinitely many solutions of the form
A) infinitely many solutions of the form
B) inconsistent system, no solution
C)
D) infinitely many solutions of the form

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck
80
A $128,000 trust is to be invested in bonds paying 9%, CDs paying 6%, and mortgages paying 10%. The sum of the bond and CD investment must equal the mortgage investment. To earn an $10,900 annual income from the
Investments, how much should the bank invest in bonds?
A) $42,000
B) $64,000
C) $20,000
D) $22,000
Investments, how much should the bank invest in bonds?
A) $42,000
B) $64,000
C) $20,000
D) $22,000

Unlock Deck
Unlock for access to all 196 flashcards in this deck.
Unlock Deck
k this deck


