Deck 5: Discrete Probability Distributions

Question 1

Sampling without replacement involves dependent events, so this would not be considered a binomial experiment. Explain the circumstances under which sampling without replacement could be considered independent and, thus, binomial.

Answer 1

When the sample size is no more than 5% of the total population size.

Question 2

Multiple-choice questions on a test each have 4 possible answers, one of which is correct. Assume that you guess the answers to 5 such questions.

A) Use the multiplication rule to find the probability that the first 2 guesses are wrong and the last 3 guesses are correct. That is, find P(WWCCC), where C denotes a correct answer and W denotes a wrong answer.
B) Make a complete list of the different possible arrangements of 2 wrong answers and 3 correct answers, then find the probability for each entry in the list.
C) Based on the preceding results, what is the probability of getting exactly 3 correct answers when 5 guesses are made?

Answer 2

a. $0.00879$

b. WWCCC
WCWCC
WCCWC
WCCCW
CWWCC
CWCWC
CWCCW
CCWWC
CCWCW
CCCWW

Each of the 10 arrangements has probability $0.00879$

c. $0.0879$

Question 3

List the two requirements for a probability histogram. Discuss the relationship between the sum of the probabilities in a probability distribution and the total area represented by the bars in a probability histogram.

Answer 3

The sum of the probabilities in a probability distribution must be 1 and each individual probability must be between 0 and 1, inclusive. The total area of the bars in a probability histogram is 1.

Question 4

Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.

-A police department reports that the probabilities that 0, 1, 2, 3, and 4 car thefts will be reported in a given day are 0.223, 0.335, 0.251, 0.126, and 0.047, respectively.

Question 5

A gambler claimed that he had loaded a die so that it would hardly ever come up 1. He said the outcomes of 1, 2, 3, 4, 5, 6 would have probabilities $$\frac { 1 } { 20 } , \frac { 1 } { 6 } , \frac { 1 } { 6 } , \frac { 1 } { 6 } , \frac { 1 } { 6 } , \frac { 1 } { 6 }$$ respectively. Can he do what he claimed? Why or why not? Is a probability distribution
described by listing the outcomes along with their corresponding probabilities? Why or why not?

Question 6

Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.

- $$\begin{array} { r | r } \mathrm { x } & \mathrm { P } ( \mathrm { x } ) \\\hline 0 & 0.157 \\1 & 0.221 \\2 & - 0.060 \\3 & 0.084 \\4 & 0.166 \\5 & 0.432\end{array}$$

Question 7

Multiple-choice questions on a test each have 6 possible answers, one of which is correct. Assume that you guess the answers to 4 such questions.

A) Use the multiplication rule to find the probability that the first two guesses are wrong and the third and fourth guesses are correct. That is, find P(WWCC), where C denotes a correct answer and W denotes a wrong answer.
B) Make a complete list of the different possible arrangements of 2 wrong answers and 2 correct answers, then find the probability for each entry in the list.
C) Based on the preceding results, what is the probability of getting exactly 2 correct answers when 4 guesses are made?

Question 8

Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.

Question 9

Assume that a probability distribution is described by the discrete random variable x that can assume the values 1, 2, . . . , n; and those values are equally likely. This probability has mean and standard deviation described as follows: $$\mu = \frac { n + 1 } { 2 } \text { and } \sigma = \sqrt { \frac { n ^ { 2 } - 1 } { 12 } }$$
$\text { Show that the formulas hold for the case of }n=7$

Question 10

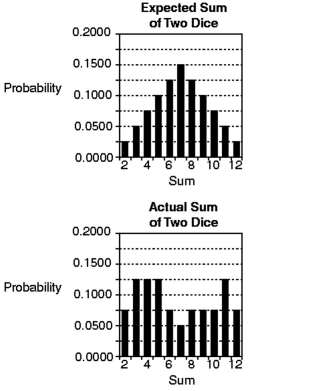
Compare the probability histogram for the expected sum with the actual results. What do you conclude about the dice results displayed in the Actual Sum of Two Dice histogram?

Question 11

Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.

-In a certain town, 50% of adults have a college degree. The accompanying table describes the probability distribution for the number of adults (among 4 randomly selected adults) who have a college degree.
$$\begin{array} { r | r } \mathrm { x } & \mathrm { P } ( \mathrm { x } ) \\\hline 0 & 0.0625 \\1 & 0.2500 \\2 & 0.3750 \\3 & 0.2500 \\4 & 0.0625\end{array}$$

Question 12

Previously, you learned to find the three important characteristics of data: the measure of central tendency, the measure of variation, and the nature of the distribution. We can find the same three characteristics for a binomial distribution. Given a binomial distribution with $\mathrm { p } = 0.4 \text { and } \mathrm { n } = 8 \text {, find the three characteristics. }$

Question 13

Identify each of the variables in the Binomial Probability Formula. $$P ( x ) = \frac { n ! } { ( n - x ) ! x ! } \cdot p ^ { x } \cdot q ^ { n - x }$$
Also, explain what the fraction $\frac { n ! } { ( n - x ) ! x ! }$ computes.

Question 14

Helene claimed that the expected value when rolling a fair die was 3.5. Steve said that wasn't possible. He said that the expected value was the most likely value in a single roll of the die, and since it wasn't possible for a die to turn up with a value of 3.5, the expected value couldn't possibly be 3.5. Who is right?

Question 15

Anna uses the letter X to represent the possible sequences of heads and tails that can be obtained when a coin is flipped three times. The possible sequences together with their probabilities are listed below:
$$\begin{array} { c | c } \mathrm { X } & \text { Probability of sequence } \mathrm { X } \\\hline \text { HHH } & 1 / 8 \\\text { HHT } & 1 / 8 \\\text { HTH } & 1 / 8 \\\text { HTT } & 1 / 8 \\\text { THH } & 1 / 8 \\\text { THT } & 1 / 8 \\\text { TTH } & 1 / 8 \\\text { TTT } & 1 / 8\end{array}$$
Is X a random variable? Why or why not? If it is not, which associated variable is a random variable? Give the probability distribution of the associated random variable.

Question 16

A game is said to be "fair" if the expected value for winnings is 0, that is, in the long run, the player can expect to win 0. Consider the following game. The game costs $1 to play and the winnings are $5 for red, $3 for blue, $2 for yellow, and nothing for white. The following probabilities apply. What are your expected winnings? Does the game favor the player or
the owner? $$\begin{array} { r | r } \text { Outcome } & \text { Probability } \\\hline \text { Red } & .02 \\\text { Blue } & .04 \\\text { Yellow } & .16 \\\text { White } & .78\end{array}$$

Question 17

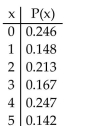
Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.

Question 18

In Hannah's school, there are 871 students of which 21% come from single-parent families.
Consider the probability that among 80 randomly selected students there are at least 20 that come from single-parent families. Can this probability be found by using the binomial probability formula? Why or why not?

Question 19

Do probability distributions measure what did happen or what will probably happen?
How do we use probability distributions to make decisions?

Question 20

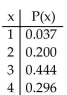
Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.

Question 21

An experiment of a gender selection method includes a control group of 8 couples who are not given any treatment intended to influence the genders of their babies. Construct a table listing the possible values of the random variable x (which represents the number of girls among the 8 births) and the corresponding probabilities. Then find the mean and standard deviation for the number of girls in such groups of 10 and the maximum and minimum usual values for the number of girls. Round all results to four decimal places.

Question 22

Suppose that in one town 10% of people are left handed. Suppose that you want to find the probability of getting exactly 2 left-handed people when 4 people are randomly selected.
Can the answer be found as follows: Use the multiplication rule to find the probability of getting two left handers followed by two right handers, which is (0.1)(0.1)(0.9)(0.9)? If not,
explain why not and show how the required probability can be found.

Question 23

Find the standard deviation, ?, for the binomial distribution which has the stated values of n and p. Round your answer to the nearest hundredth.

- $\mathrm { n } = 693 ; \mathrm { p } = 0.7$

A) $\sigma = 16.18$
B) $\sigma = 9.65$
C) $\sigma = 12.06$
D) $\sigma = 15.33$

Question 24

Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
Rolling a single "loaded" die 11 times, keeping track of the numbers that are rolled.

A) Not binomial: the trials are not independent.
B) Not binomial: there are more than two outcomes for each trial.
C) Procedure results in a binomial distribution.
D) Not binomial: there are too many trials.

Question 25

List the four requirements for a binomial distribution. Describe an experiment which is binomial and discuss how the experiment fits each of the four requirements.

Question 26

Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.

-If a person is randomly selected from a certain town, the probability distribution for the number, x, of siblings is as described in the accompanying table.
$$\begin{array} { c | c } \mathrm { x } & \mathrm { P } ( \mathrm { x } ) \\\hline 0 & 0.27 \\1 & 0.28 \\2 & 0.23 \\3 & 0.10 \\4 & 0.06 \\5 & 0.02\end{array}$$

Question 27

Suppose a mathematician computed the expected value of winnings for a person playing each of seven different games in a casino. What would you expect to be true for all expected values for these seven games?

Question 28

Focus groups of 11 people are randomly selected to discuss products of the Famous Company. It is determined that the mean number (per group) who recognize the Famous brand name is 5.7, and The standard deviation is 0.50. Would it be unusual to randomly select 11 people and find that Greater than 9 recognize the Famous brand name?

A) Yes
B) No

Question 29

Find the indicated probability. Round to three decimal places.

-An airline estimates that 91% of people booked on their flights actually show up. If the airline books 76 people on a flight for which the maximum number is 74, what is the probability that the Number of people who show up will exceed the capacity of the plane?

A) 0.028
B) 0.006
C) 0.007
D) 0.001

Question 30

Assume that a procedure yields a binomial distribution with a trial repeated n times. Use the binomial probability
formula to find the probability of x successes given the probability p of success on a single trial. Round to three decimal
places.

- $\mathrm { n } = 4 , \mathrm { x } = 3 , \mathrm { p } = \frac { 1 } { 6 }$

A) 0.012
B) 0.015
C) 0.004
D) 0.023

Question 31

Find the mean of the given probability distribution.

- $\begin{array}{c|c}\mathrm{x} & \mathrm{P}(\mathrm{x}) \\\hline 0 & 0.23 \\1 & 0.20 \\2 & 0.37 \\3 & 0.06 \\4 & 0.14\end{array}$

A) $\mu = 1.81$
B) $\mu = 1.68$
C) $\mu = 1.58$
D) $\mu = 1.91$

Question 32

If a procedure meets all the conditions of a binomial distribution except that the number of trials is not fixed, then the geometric distribution can be used. The probability of getting the first success on The xth trial is given by $P ( x ) = p ( 1 - p ) ^ { x - 1 }$ , where p is the probability of success on any one trial.Assume that the probability of choosing a yellow piece of candy in a bag of hard candy is 0.240.
Find the probability that the first yellow candy is found in the fourth inspected. Round your answer to the nearest thousandth.

A) 0.08
B) 0.061
C) 0.439
D) 0.105

Question 33

List the three methods for finding binomial probabilities in the table below, and then complete the table to discuss the advantages and disadvantages of each.
$$\begin{array} { | l | l | l | } \hline \text { Methods } & \text { Advantage } & \text { Disadvantage } \\\hline & & \\\hline & & \\\hline & & \\\hline & & \\\hline\end{array}$$

Question 34

Find the mean of the given probability distribution.

-The probabilities that a batch of 4 computers will contain 0, 1, 2, 3, and 4 defective computers are 0.6561, 0.2916, 0.0486, 0.0036, and 0.0001, respectively. Round answer to the nearest hundredth.

A) $\mu = 0.30$
B) $\mu = 2.00$
C) $\mu = 1.06$
D) $\mu = 0.40$

Question 35

Use the given values of n and p to find the minimum usual value $\mu - 2 \sigma$ and the maximum usual value $\mu + 2 \sigma$ . Round your answer to the nearest hundredth unless otherwise noted.

- $n = 460 , p = \frac { 2 } { 7 }$

A) Minimum: 112.05; maximum: 150.81
B) Minimum: 121.74; maximum: 141.12
C) Minimum: 150.81; maximum: 112.05
D) Minimum: 117.73; maximum: 145.13

Question 36

Find the indicated probability. Round to three decimal places.

-A car insurance company has determined that 8% of all drivers were involved in a car accident last year. Among the 14 drivers living on one particular street, 3 were involved in a car accident last year. If 14 drivers are randomly selected, what is the probability of getting 3 or more who were involved in a car accident last year?

A) 0.074
B) 0.926
C) 0.407
D) 0.096

Question 37

A multiple choice test has 7 questions each of which has 5 possible answers, only one of which is correct. If Judy, who forgot to study for the test, guesses on all questions, what is the probability That she will answer exactly 3 questions correctly?

A) 0.115
B) 0.885
C) 0.275
D) 0.00800

Question 38

In a certain town, 90 percent of voters are in favor of a given ballot measure and 10 percent are opposed. For groups of 260 voters, find the mean for the number who oppose the measure.

A) 26
B) 90
C) 10
D) 234

Question 39

A 28-year-old man pays $118 for a one-year life insurance policy with coverage of $140,000. If the probability that he will live through the year is 0.9993, what is the expected value for the insurance
Policy?

A) $139,902.00
B) -$20.00
C) -$117.92
D) $98.00

Question 40

The brand name of a certain chain of coffee shops has a 50% recognition rate in the town of Coffleton. An executive from the company wants to verify the recognition rate as the company is Interested in opening a coffee shop in the town. He selects a random sample of 9 Coffleton Residents. Find the probability that the number that recognize the brand name is not 4.

A) 0.754
B) 0.164
C) 0.246
D) 0.00195

Question 41

Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
Spinning a roulette wheel 6 times, keeping track of the occurrences of a winning number of "16".

A) Not binomial: there are more than two outcomes for each trial.
B) Not binomial: the trials are not independent.
C) Not binomial: there are too many trials.
D) Procedure results in a binomial distribution..

Question 42

Find the mean, µ, for the binomial distribution which has the stated values of n and p. Round answer to the nearest tenth.

- $\mathrm { n } = 625 ; \mathrm { p } = 0.7$

A) $\mu = 436.0$
B) $\mu = 437.5$
C) $\mu = 438.8$
D) $\mu = 439.2$

Question 43

Find the mean of the given probability distribution.

-In a certain town, 40% of adults have a college degree. The accompanying table describes the probability distribution for the number of adults (among 4 randomly selected adults) who have a college degree.

$\begin{array}{c|r}\mathrm{x} & \mathrm{P}(\mathrm{x}) \\\hline 0 & 0.1296 \\1 & 0.3456 \\2 & 0.3456 \\3 & 0.1536 \\4 & 0.0256\end{array}$

A) $\mu = 2.00$
B) $\mu = 1.50$
C) $\mu = 1.60$
D) $\mu = 1.73$

Question 44

Choosing 5 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green) one at a time without replacement, keeping track of the number of red marbles chosen.

A) Procedure results in a binomial distribution.
B) Not binomial: there are more than two outcomes for each trial.
C) Not binomial: there are too many trials.
D) Not binomial: the trials are not independent.

Question 45

Suppose that weight of adolescents is being studied by a health organization and that the accompanying tables describes the probability distribution for three randomly selected adolescents, where x is the number who are considered morbidly obese. Is it unusual to have no obese subjects
Among three randomly selected adolescents? $$\begin{array} { c | c } \mathrm { x } & \mathrm { P } ( \mathrm { x } ) \\\hline 0 & 0.111 \\1 & 0.215 \\2 & 0.450 \\3 & 0.224\end{array}$$

A) Yes
B) No

Question 46

Identify the given random variable as being discrete or continuous.
The number of field goals kicked in a football game

A) Continuous
B) Discrete

Question 47

Assume that a researcher randomly selects 14 newborn babies and counts the number of girls selected, x. The probabilities corresponding to the 14 possible values of x are summarized in the given table. Answer the question using
the table.
$$\begin{array}{l}\text {\quad\quad\quad\quad\quad\quad\quad\quad Probabilities of Girls }\\\begin{array} { c | c | c | c | c | c } x ( \text { girls) } & P ( x ) & x \text { (girls) } & P ( x ) & x \text { (girls) } & P ( x ) \\\hline 0 & 0.000 & 5 & 0.122 & 10 & 0.061 \\1 & 0.001 & 6 & 0.183 & 11 & 0.022 \\2 & 0.006 & 7 & 0.209 & 12 & 0.006 \\3 & 0.022 & 8 & 0.183 & 13 & 0.001 \\4 & 0.061 & 9 & 0.122 & 14 & 0.000\end{array}\end{array}$$

-Find the probability of selecting exactly 4 girls.

A) 0.122
B) 0.061
C) 0.022
D) 0.001

Question 48

Use the given values of n and p to find the minimum usual value µ - 2? and the maximum usual value µ + 2?. Round your answer to the nearest hundredth unless otherwise noted.

- $$\mathrm { n } = 2428 , \mathrm { p } = 0.577 \text { Round your answers to the nearest thousandth. }$$

A) Minimum: 1352.269; maximum: 1449.643
B) Minimum: 1366.529; maximum: 1435.383
C) Minimum: 1449.643; maximum: 1352.269
D) Minimum: 1376.613; maximum: 1425.299

Question 49

Identify the given random variable as being discrete or continuous.
The number of oil spills occurring off the Alaskan coast

A) Continuous
B) Discrete

Question 50

Assume that $\mathrm { x }$ is a random variable in a probability distribution with mean $\mu$ and standard deviation $\sigma$ . Find expressions for the mean and standard deviation if every value of $\mathrm { x }$ is modified by first being multiplied by 5 , then increased by 4 .

A) $\mu _ { \text {new } } = 5 \mu + 4 ; \sigma _ { \text {new } } = 5 \sigma + 4$
B) $\mu _ { \text {new } } = 4 \mu + 5 ; \sigma _ { \text {new } } = 4 \sigma$
C) $\mu _ { \text {new } } = \mu + 4 ; \sigma _ { \text {new } } = 5 \sigma$
D) $\mu _ { \text {new } } = 5 \mu + 4 ; \sigma _ { \text {new } } = 5 \sigma$

Question 51

Suppose that voting in municipal elections is being studied and that the accompanying tables describes the probability distribution for four randomly selected people, where x is the number that voted in the last election. Is it unusual to find four voters among four randomly selected people?
$$\begin{array} { c | c } \mathrm { x } & \mathrm { P } ( \mathrm { x } ) \\\hline 0 & 0.23 \\1 & 0.32 \\2 & 0.26 \\3 & 0.15 \\4 & 0.04\end{array}$$

A) Yes
B) No

Question 52

Identify the given random variable as being discrete or continuous.
The cost of a randomly selected orange

A) Discrete
B) Continuous

Question 53

Determine if the outcome is unusual. Consider as unusual any result that differs from the mean by more than 2 standard deviations. That is, unusual values are either less than µ - 2? or greater than µ + 2?.

-According to AccuData Media Research, 36% of televisions within the Chicago city limits are tuned to "Eyewitness News" at 5:00 pm on Sunday nights. At 5:00 pm on a given Sunday, 2500 such televisions are randomly selected and checked to determine what is being watched. Would it be
Unusual to find that 900 of the 2500 televisions are tuned to "Eyewitness News"?

A) Yes
B) No

Question 54

Find the standard deviation, ?, for the binomial distribution which has the stated values of n and p. Round your answer to the nearest hundredth.

- $\mathrm { n } = 41 ; \mathrm { p } = 0.2$

A) $\sigma = 0.15$
B) $\sigma = 5.83$
C) $\sigma = 6.68$
D) $\sigma = 2.56$

Question 55

In a game, you have a 1/20 probability of winning $76 and a 19/20 probability of losing $9. What is your expected value?

A) $12.35
B) -$8.55
C) $3.80
D) -$4.75

Question 56

Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
Choosing 8 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green) one at a time with replacement, keeping track of the colors of the marbles chosen.

A) Not binomial: the trials are not independent.
B) Not binomial: there are too many trials.
C) Procedure results in a binomial distribution.
D) Not binomial: there are more than two outcomes for each trial.

Question 57

A die is rolled 9 times and the number of times that two shows on the upper face is counted. If this experiment is repeated many times, find the mean for the number of twos.

A) 3
B) 2.25
C) 7.5
D) 1.5

Question 58

Assume that a researcher randomly selects 14 newborn babies and counts the number of girls selected, x. The probabilities corresponding to the 14 possible values of x are summarized in the given table. Answer the question using
the table.
$$\begin{array}{l}\text {\quad\quad\quad\quad\quad\quad\quad\quad Probabilities of Girls }\\\begin{array} { c | c | c | c | c | c } x ( \text { girls) } & P ( x ) & x \text { (girls) } & P ( x ) & x \text { (girls) } & P ( x ) \\\hline 0 & 0.000 & 5 & 0.122 & 10 & 0.061 \\1 & 0.001 & 6 & 0.183 & 11 & 0.022 \\2 & 0.006 & 7 & 0.209 & 12 & 0.006 \\3 & 0.022 & 8 & 0.183 & 13 & 0.001 \\4 & 0.061 & 9 & 0.122 & 14 & 0.000\end{array}\end{array}$$

-Find the probability of selecting exactly 5 girls.

A) 0.022
B) 0.122
C) 0.001
D) 0.061

Question 59

Provide an appropriate response. Round to the nearest hundredth.

-The probabilities that a batch of 4 computers will contain 0, 1, 2, 3, and 4 defective computers are 0.6561, 0.2916, 0.0486, 0.0036, and 0.0001, respectively. Find the standard deviation for the probability distribution.

A) $\sigma = 0.60$
B) $\sigma = 0.36$
C) $\sigma = 0.72$
D) $\sigma = 0.53$

Question 60

Find the mean, µ, for the binomial distribution which has the stated values of n and p. Round answer to the nearest tenth.

- $n = 2515 ; p = 0.63$

A) $\mu = 1579.2$
B) $\mu = 1584.5$
C) $\mu = 1588.2$
D) $\mu = 1576.0$

Question 61

The probability of winning a certain lottery is $\frac { 1 } { 76,394 }$ For people who play 987 times, find the mean number of wins.

A) 0.0129
B) 0.000013
C) 77.4
D) 0.0010

Question 62

Provide an appropriate response. Round to the nearest hundredth.

-The random variable x is the number of houses sold by a realtor in a single month at the Sendsom's Real Estate Office. Its probability distribution is as follows. Find the standard deviation for the probability distribution.

$\begin{array}{c|c}\text { Houses Sold }(\mathrm{x}) & \text { Probability } \mathrm{P}(\mathrm{x}) \\\hline 0 & 0.24 \\1 & 0.01 \\2 & 0.12 \\3 & 0.16 \\4 & 0.01 \\5 & 0.14 \\6 & 0.11 \\7 & 0.21\end{array}$

A) $\sigma = 2.25$
B) $\sigma = 4.45$
C) $\sigma = 6.86$
D) $\sigma = 2.62$

Question 63

Find the indicated probability. Round to three decimal places.

-A machine has 12 identical components which function independently. The probability that a component will fail is 0.2. The machine will stop working if more than three components fail. Find the probability that the machine will be working.

A) 0.927
B) 0.133
C) 0.795
D) 0.206

Question 64

Assume that there is a 0.05 probability that a sports playoff series will last four games, a 0.45 probability that it will last five games, a 0.45 probability that it will last six games, and a 0.05 probability that it will last seven games. Is it unusual for a team to win a series in 7 games?

A) Yes
B) No

Question 65

Find the indicated probability.

-The brand name of a certain chain of coffee shops has a 57% recognition rate in the town of Coffleton. An executive from the company wants to verify the recognition rate as the company is interested in opening a coffee shop in the town. He selects a random sample of 10 Coffleton residents. Find the probability that exactly 4 of the 10 Coffleton residents recognize the brand name.

A) 0.106
B) 0.0604
C) 0.000667
D) 0.140

Question 66

Suppose that computer literacy among people ages 40 and older is being studied and that the accompanying tables describes the probability distribution for four randomly selected people, where x is the number that are computer literate. Is it unusual to find four computer literates among four randomly selected people?
$$\begin{array} { c | c } \mathrm { x } & \mathrm { P } ( \mathrm { x } ) \\\hline 0 & 0.16 \\1 & 0.25 \\2 & 0.36 \\3 & 0.15 \\4 & 0.08\end{array}$$

A) Yes
B) No

Question 67

Suppose you buy 1 ticket for $1 out of a lottery of 1,000 tickets where the prize for the one winning ticket is to be $500. What is your expected value?

A) $- \$ 1.00$
B) $- \$ 0.40$
C) $\$ 0.00$
D) $- \$ 0.50$

Question 68

Use the given values of n and p to find the minimum usual value $\mu - 2 \sigma \text { and the maximum usual value } \mu + 2 \sigma$ . Round your answer to the nearest hundredth unless otherwise noted.

- $n = 659 , p = \frac { 4 } { 5 }$

A) Minimum: 516.93; maximum: 537.47
B) Minimum: 506.66; maximum: 547.74
C) Minimum: 465.59; maximum: 588.81
D) Minimum: 547.74; maximum: 506.66

Question 69

Find the mean, µ, for the binomial distribution which has the stated values of n and p. Round answer to the nearest tenth.

- $\mathrm { n } = 32 ; \mathrm { p } = 3 / 5$

A) $\mu = 19.5$
B) $\mu = 18.7$
C) $\mu = 19.2$
D) $\mu = 19.9$

Question 70

A company manufactures calculators in batches of 55 and claims that the rate of defects is 4%. Find the probability of getting exactly 2 defects in a batch of 55 if the rate of defects is 4%. If a store receives a batch of 55 calculators and finds that there are 2 defective calculators, do they have any reason to doubt the company's claimed rate of defects?

A) 0.0181; Yes. If the rate of defects is really 4%, the probability of finding 2 defects in a batch of 55 calculators is very small.
B) 0.546; No. If the rate of defects is really 4%, it is not so unlikely to find 2 defects in a batch of 55 calculators.
C) 0.273; No. If the rate of defects is really 4%, it is not so unlikely to find 2 defects in a batch of 55 calculators.
D) 0.262; No. If the rate of defects is really 4%, it is not so unlikely to find 2 defects in a batch of 55 calculators.

Question 71

The binomial distribution applies only to cases involving two types of outcomes, whereas the multinomial distribution involves more than two categories. Suppose we have three types of mutually exclusive outcomes denoted by $\mathrm { A } , \mathrm { B }$ , and $\mathrm { C }$ . Let $\mathrm { P } ( \mathrm { A } ) = \mathrm { p } _ { 1 } , \mathrm { P } ( \mathrm { B } ) = \mathrm { p } _ { 2 } , \mathrm { P } ( \mathrm { C } ) = \mathrm { p } _ { 3 }$ . In $n$ independent trials, the probability of $\mathrm { x } _ { 1 }$ outcomes of type $\mathrm { A } , \mathrm { x } _ { 2 }$ outcomes of type $\mathrm { B }$ , and $\mathrm { x } _ { 3 }$ outcomes of type $\mathrm { C }$ is given by
$$\frac { n ! } { \left( x _ { 1 } \right) ! \left( x _ { 2 } \right) ! \left( x _ { 3 } \right) ! } \cdot p _ { 1 } { } ^ { x _ { 1 } } \cdot p _ { 2 } { } ^ { x _ { 2 } } \cdot p _ { 3 } { } ^ { x _ { 3 } }$$ A genetics experiment involves four mutually exclusive genotypes identified as A, B, C, and D, and they are all equally likely. If 13 offspring are tested, find the probability of getting exactly 3 A's,2 B's,3 C's, and 5 D's by expanding the above expression so that it applies to four types of outcomes instead of only three. Round your answer to five decimal places.

A) 1.28875
B) 0.01074
C) 0.00268
D) 0.04296

Question 72

Assume that a procedure yields a binomial distribution with a trial repeated n times. Use the binomial probability formula to find the probability of x successes given the probability p of success on a single trial. Round to three decimal places.

- $n = 64 , x = 3 , p = 0.04$

A) 0.091
B) 0.375
C) 0.221
D) 0.139

Question 73

Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
Spinning a roulette wheel 5 times, keeping track of the winning numbers.

A) Not binomial: there are too many trials.
B) Procedure results in a binomial distribution.
C) Not binomial: the trials are not independent.
D) Not binomial: there are more than two outcomes for each trial.

Question 74

A police department reports that the probabilities that 0, 1, 2, and 3 burglaries will be reported in a given day are 0.50, 0.38, 0.10, and 0.02, respectively. Find the standard deviation for the probability distribution. Round answer to the nearest hundredth.

A) $\sigma = 0.55$
B) $\sigma = 1.02$
C) $\sigma = 0.74$
D) $\sigma = 0.98$

Question 75

Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
Choosing 5 people (without replacement) from a group of 23 people, of which 15 are women, keeping track of the number of men chosen.

A) Procedure results in a binomial distribution.
B) Not binomial: the trials are not independent.
C) Not binomial: there are too many trials.
D) Not binomial: there are more than two outcomes for each trial.

Question 76

Identify the given random variable as being discrete or continuous.
The number of phone calls between New York and California on Thanksgiving day

A) Continuous
B) Discrete

Question 77

Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
Rolling a single die 36 times, keeping track of the "fives" rolled.

A) Not binomial: the trials are not independent.
B) Not binomial: there are too many trials.
C) Procedure results in a binomial distribution.
D) Not binomial: there are more than two outcomes for each trial.

Question 78

Determine if the outcome is unusual. Consider as unusual any result that differs from the mean by more than 2 standard deviations. That is, unusual values are either less than µ - 2? or greater than µ + 2?.

-The Acme Candy Company claims that 60% of the jawbreakers it produces weigh more than .4 ounces. Suppose that 800 jawbreakers are selected at random from the production lines. Would it be unusual for this sample of 800 to contain 423 jawbreakers that weigh more than .4 ounces?

A) Yes
B) No

Question 79

Find the mean of the given probability distribution.

-The accompanying table shows the probability distribution for $x$ , the number that shows up when a loaded die is rolled.
$\begin{array}{c|c}x & P(x) \\\hline 1 & 0.12 \\2 & 0.15 \\3 & 0.13 \\4 & 0.11 \\5 & 0.12 \\6 & 0.37\end{array}$

A) $\mu = 3.50$
B) $\mu = 4.07$
C) $\mu = 0.17$
D) $\mu = 3.94$

Question 80

Find the indicated probability.
Suppose that 10% of people are left handed. If 6 people are selected at random, what is the probability that exactly 2 of them are left handed?

A) 0.0984
B) 0.197
C) 0.0100
D) 0.0146