Deck 2: Systems of Linear Equations and Matrices
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/110
Play
Full screen (f)
Deck 2: Systems of Linear Equations and Matrices
1
An m × n zero matrix serves as an m × n .
additive identity
2

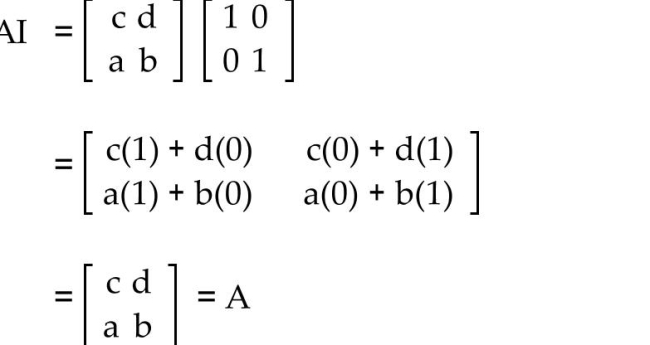
3
Use a graphing calculator to solve the system of equations. Round your solution to one decimal place.
A)
B)
C)
D)
A)
B)
C)
D)
4
Provide an appropriate response
Which choice best describes the following matrix?
Which choice best describes the following matrix?


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
5
Perform the indicated operation, where possible.
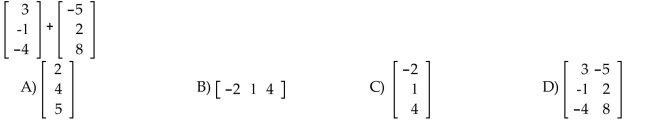
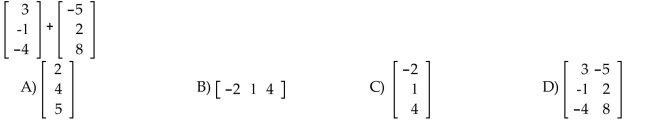

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
6
Use the Gauss-Jordan method to solve the system of equations.
A)
B)
C)
D) No solution
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the problem.
16)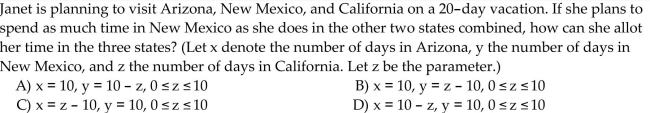
16)
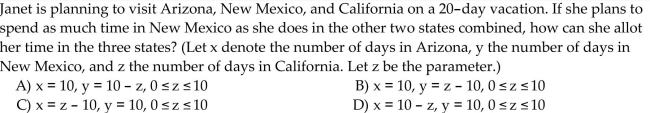

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
8
Does a matrix with a column of all zeros have an inverse? Why or why not?

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
9
Use the Gauss-Jordan method to solve the system of equations.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
10
The property does not apply to matrix multiplication.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
11

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
12
If a variable is expressed in terms of another variable, what is the other variable called?

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
13
How many solutions are there to a dependent system?

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
14
Describe the proper form for the system to be in before the Gauss-Jordan method can be used.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
15
Use a graphing calculator to solve the system of equations. Round your solution to one decimal place.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
16
Use the echelon method to solve the system.
A)
B)
C)
D) No solution
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
17
Can non-square matrices have inverses? Why or why not?

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
18
Use the Gauss-Jordan method to solve the system of equations.
A)
B)
C)
D) No solution
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
19
Use the Gauss-Jordan method to solve the system of equations.
A) (-1,4,-5,2)
B) (2,3,-4,-2)
C) (2,-3,4,-1)
D) No solution
A) (-1,4,-5,2)
B) (2,3,-4,-2)
C) (2,-3,4,-1)
D) No solution

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
20
Is this a square matrix? Why or why not? 


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
21
Find the matrix product, if possible.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the problem.
A company makes three chocolate candies: cherry, almond, and raisin. Matrix A gives the amount of ingredients in one batch. Matrix B gives the costs of ingredients from suppliers J and K. What is
The cost of 100 batches of each candy using ingredients from supplier J?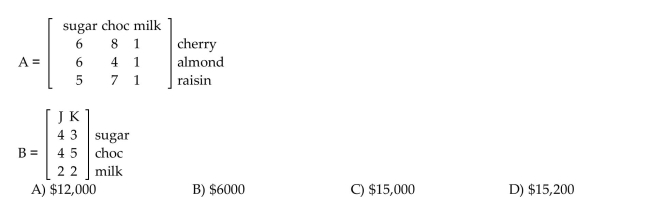
A company makes three chocolate candies: cherry, almond, and raisin. Matrix A gives the amount of ingredients in one batch. Matrix B gives the costs of ingredients from suppliers J and K. What is
The cost of 100 batches of each candy using ingredients from supplier J?
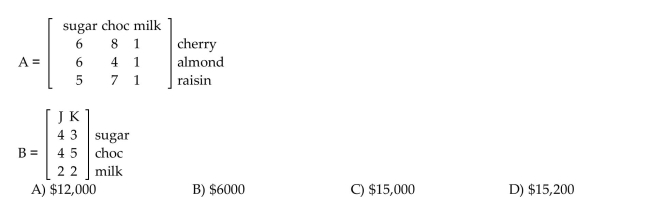

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the problem.
-A basketball fieldhouse seats 15,000. Courtside seats cost $10, endzone seats cost $6, and balcony seats cost $4. The total revenue for a sellout is $82,000. If half the courtside seats, half the balcony Seats, and all the endzone seats are sold; then the total revenue is $47,000. How many of each type Of seat are there?
A)4000 courtside, 3000 endzone, 8000 balcony
B)3000 courtside, 4000 endzone, 8000 balcony
C)3000 courtside, 2000 endzone, 10,000 balcony
D)3200 courtside, 1800 endzone, 10,000 balcony
-A basketball fieldhouse seats 15,000. Courtside seats cost $10, endzone seats cost $6, and balcony seats cost $4. The total revenue for a sellout is $82,000. If half the courtside seats, half the balcony Seats, and all the endzone seats are sold; then the total revenue is $47,000. How many of each type Of seat are there?
A)4000 courtside, 3000 endzone, 8000 balcony
B)3000 courtside, 4000 endzone, 8000 balcony
C)3000 courtside, 2000 endzone, 10,000 balcony
D)3200 courtside, 1800 endzone, 10,000 balcony

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
24
Decide whether the matrices are inverses of each other. (Check to see if their product is the identity matrix I.) and

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
25
Find the matrix product, if possible.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
26
Use the Gauss-Jordan method to solve the system of equations.
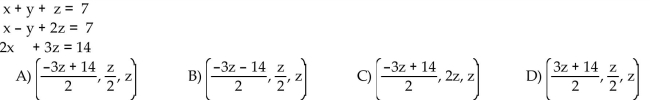
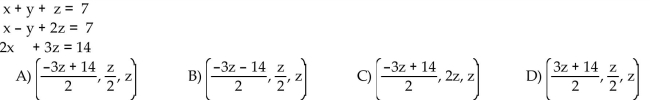

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the system of equations. Let z be the parameter.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
28
Perform the indicated operation, where possible.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the problem.
-A company makes three chocolate candies: cherry, almond, and raisin. Matrix A gives the amount of ingredients in one batch. Matrix B gives the costs of ingredients from suppliers X and Y. What is The cost of 100 batches of each candy using ingredients from supplier X?
A)
B)
C)
D)
-A company makes three chocolate candies: cherry, almond, and raisin. Matrix A gives the amount of ingredients in one batch. Matrix B gives the costs of ingredients from suppliers X and Y. What is The cost of 100 batches of each candy using ingredients from supplier X?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
30
Use the echelon method to solve the system of two equations in two unknowns.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
31
Decide whether the matrices are inverses of each other. (Check to see if their product is the identity matrix I.)



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
32
Use the indicated row operation to change the matrix.
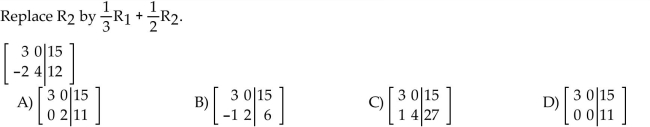
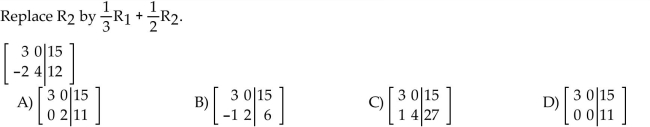

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
33
Find the value.
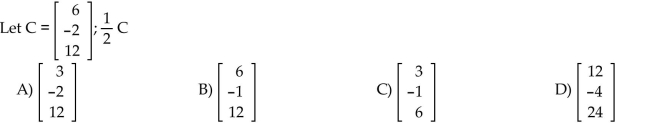
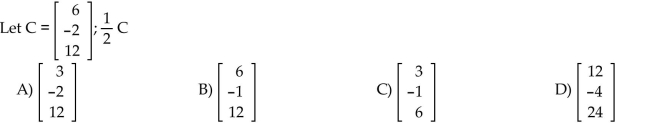

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
34
Write the system of equations associated with the augmented matrix.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
35
Use the echelon method to solve the system.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
36
Find the values of the variables in the equation.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the system of equations by using the inverse of the coefficient matrix if it exists and by the echelon method if the
inverse doesn't exist.

inverse doesn't exist.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
38
Decide whether the matrices are inverses of each other. (Check to see if their product is the identity matrix I.) and

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
39
Use a graphing calculator to solve the system of equations. Round your solution to one decimal place. and

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the problem.
The matrices give points and rebounds for five starting players in two games. Find the matrix that gives the totals.
The matrices give points and rebounds for five starting players in two games. Find the matrix that gives the totals.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
41
The sizes of two matrices A and B are given. Find the sizes of the product AB and the product BA, whenever these
products exist.

products exist.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
42
Use a graphing calculator to find the matrix product and/or sum.
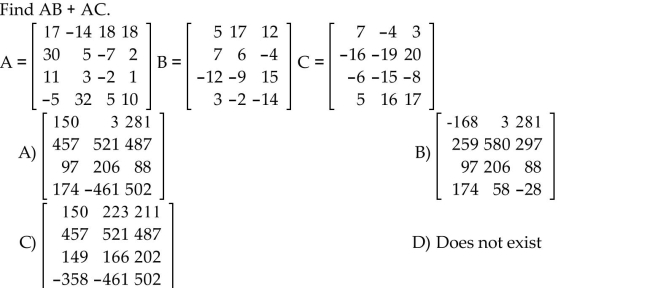


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
43
The sizes of two matrices A and B are given. Find the sizes of the product AB and the product BA, whenever these
products exist.

products exist.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the system of equations by using the inverse of the coefficient matrix if it exists and by the echelon method if the
inverse doesn't exist.

inverse doesn't exist.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.
-An investor has $400,000 to invest in stocks, bonds, and commodities. If he plans to put three times as much into stocks as in bonds, how can he distribute his money among the three types of Investments? (Let x denote the amount put into stocks, y the amount put into bonds, and z the Amount put into commodities. Let all amounts be in dollars, and let z be the parameter.)
A)
B)
C)
D)
-An investor has $400,000 to invest in stocks, bonds, and commodities. If he plans to put three times as much into stocks as in bonds, how can he distribute his money among the three types of Investments? (Let x denote the amount put into stocks, y the amount put into bonds, and z the Amount put into commodities. Let all amounts be in dollars, and let z be the parameter.)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the problem.
Carney and Dobler sell auto and hazard insurance. Their sales, in dollars, for the months of July and August are given in the following matrices.
Carney and Dobler sell auto and hazard insurance. Their sales, in dollars, for the months of July and August are given in the following matrices.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
47
The sizes of two matrices A and B are given. Find the sizes of the product AB and the product BA, whenever these products exist.
- is , and B is .
A)
B) ; BA does not exist.
C) does not exist:
D)
- is , and B is .
A)
B) ; BA does not exist.
C) does not exist:
D)

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
48
Find the inverse, if it exists, for the matrix.
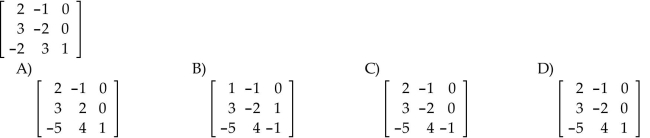


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
49
Find the matrix product, if possible.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the problem.
Anne and Nancy use a metal alloy that is 25.75% copper to make jewelry. How many ounces of a 19% alloy must be mixed with a 28% alloy to form 92 ounces of the desired alloy?
A)25 ounces
B)23 ounces
C)74 ounces
D)69 ounces
Anne and Nancy use a metal alloy that is 25.75% copper to make jewelry. How many ounces of a 19% alloy must be mixed with a 28% alloy to form 92 ounces of the desired alloy?
A)25 ounces
B)23 ounces
C)74 ounces
D)69 ounces

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
51
Find the inverse, if it exists, for the matrix.
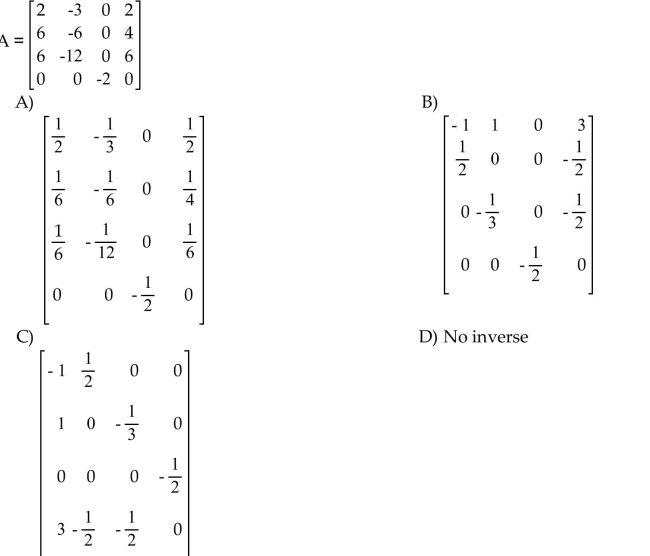


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
52
Write a matrix to display the information.
-A bakery sells three types of cakes. Cake I requires 2 cups of flour, 2 cups of sugar, and 2 eggs. Cake II requires 4 cups of flour, 1 cup of sugar, and 1 egg. Cake III requires 2 cups of flour, 2 cups of Sugar, and 3 eggs. Make a 3 × 3 matrix showing the required ingredients for each cake. Assign the
Cakes to the rows and the ingredients to the columns.
A)
B)
C)
D)
-A bakery sells three types of cakes. Cake I requires 2 cups of flour, 2 cups of sugar, and 2 eggs. Cake II requires 4 cups of flour, 1 cup of sugar, and 1 egg. Cake III requires 2 cups of flour, 2 cups of Sugar, and 3 eggs. Make a 3 × 3 matrix showing the required ingredients for each cake. Assign the
Cakes to the rows and the ingredients to the columns.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
53
Find the ratios of products A, B, and C using a closed model.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
54
Find the matrix product, if possible.
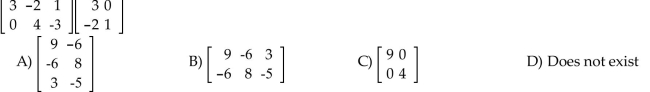
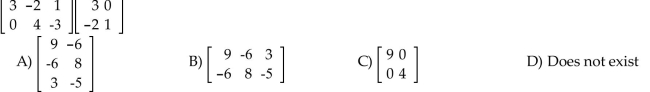

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
55
Provide an appropriate response.
What are the elements of the third row of the following matrix? 42)
What are the elements of the third row of the following matrix? 42)


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
56
Decide whether the matrices are inverses of each other. (Check to see if their product is the identity matrix I.)
- and
- and

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the system of equations by using the inverse of the coefficient matrix.
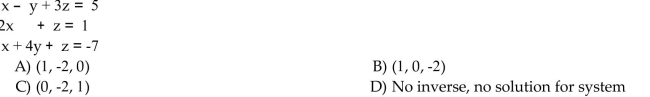
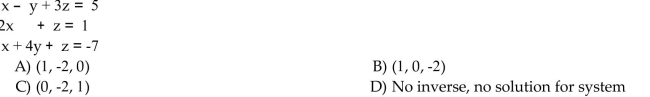

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
58
Find the ratios of products A, B, and C using a closed model.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
59
Find the matrix product, if possible.
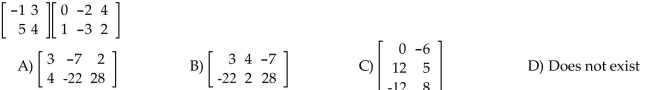
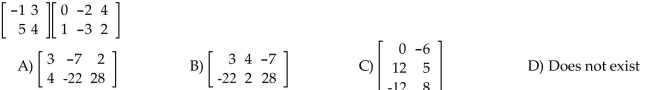

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
60
Find the inverse, if it exists, for the matrix.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
61
Use a graphing calculator to solve the system of equations. Round your solution to one decimal place.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
62
Use the Gauss-Jordan method to solve the system of equations.
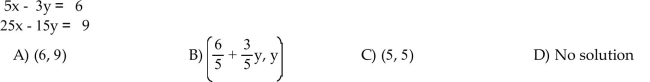
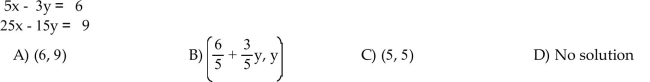

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
63
Find the ratios of products A, B, and C using a closed model.
-
A) 13: 25: 100
B)
C) 1:
D) 1: 25: 25
-

A) 13: 25: 100
B)
C) 1:
D) 1: 25: 25

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the system of equations by using the inverse of the coefficient matrix if it exists and by the echelon method if the inverse doesn't exist.
-
A)
B)
C)
D) No inverse, no solution for system
-
A)
B)
C)
D) No inverse, no solution for system

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
65
Find the production matrix for the input-output and demand matrices using the open model.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the problem.
-A company makes three chocolate candies: cherry, almond, and raisin. Matrix A gives the amount of ingredients in one batch. Matrix B gives the costs of ingredients from suppliers J and K. What is The cost of 100 batches of each candy using ingredients from supplier K?

A)
B)
C)
D)
-A company makes three chocolate candies: cherry, almond, and raisin. Matrix A gives the amount of ingredients in one batch. Matrix B gives the costs of ingredients from suppliers J and K. What is The cost of 100 batches of each candy using ingredients from supplier K?

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
67
Solve the problem.
Suppose the following matrix represents the input-output matrix, T, of a simplified economy. Find the amount of each commodity that should be produced.
Find the amount of each commodity that should be produced.
A)3360 units of manufacturing, 2796 units of agriculture, and 3012 units of transportation.
B)2976 units of manufacturing, 3386.4 units of agriculture, and 2791.2 units of transportation.
C)3012 units of manufacturing, 3360 units of agriculture, and 2791.2 units of transportation.
D)3012 units of manufacturing, 2796 units of agriculture, and 2976 units of transportation.
Suppose the following matrix represents the input-output matrix, T, of a simplified economy.
 Find the amount of each commodity that should be produced.
Find the amount of each commodity that should be produced.A)3360 units of manufacturing, 2796 units of agriculture, and 3012 units of transportation.
B)2976 units of manufacturing, 3386.4 units of agriculture, and 2791.2 units of transportation.
C)3012 units of manufacturing, 3360 units of agriculture, and 2791.2 units of transportation.
D)3012 units of manufacturing, 2796 units of agriculture, and 2976 units of transportation.

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
68
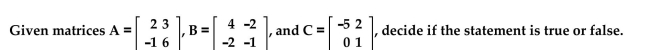
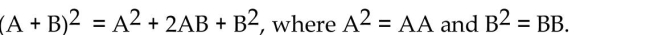

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the system of equations by using the inverse of the coefficient matrix.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
70
Find the ratios of products A, B, and C using a closed model.
-
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
71
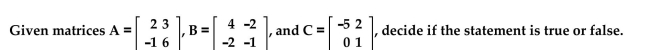
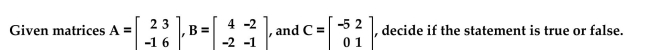 AB is a 2 × 2 matrix.
AB is a 2 × 2 matrix.
Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
72
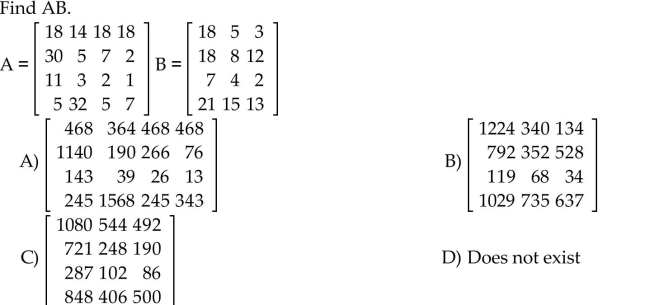
Use a graphing calculator to find the matrix product and/or sum.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
73
Use the Gauss-Jordan method to solve the system of equations.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
74
For the following systems of equations in echelon form, tell how many solutions there are in nonnegative integers.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
75
Find the inverse, if it exists, for the matrix.
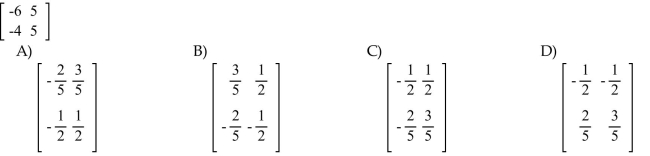
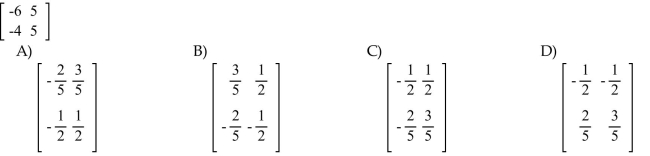

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
76
Find the ratios of products A, B, and C using a closed model.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the system of equations by using the inverse of the coefficient matrix.



Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
78
Provide an appropriate response.
True or False?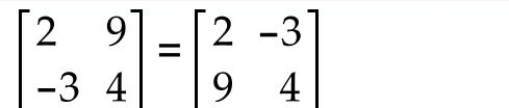
True or False?
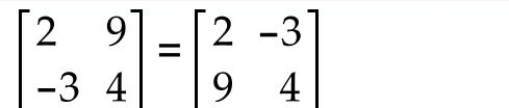

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
79
Use the indicated row operation to change the matrix.
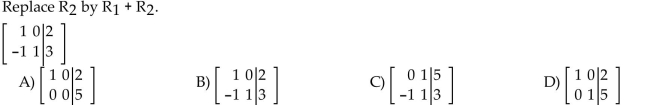
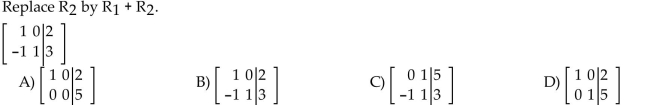

Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck
80
Use a graphing calculator to find the matrix product and/or sum.
Find BA.
Find BA.


Unlock Deck
Unlock for access to all 110 flashcards in this deck.
Unlock Deck
k this deck


