Deck 6: Rational Expressions, Functions, and Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/102
Play
Full screen (f)
Deck 6: Rational Expressions, Functions, and Equations
1
Find the function value.
A) 0
B) 1
C)
D) 3
A) 0
B) 1
C)
D) 3
D
2
The graph of a rational function, f, is shown in the figure. Use the graph to answer the question. 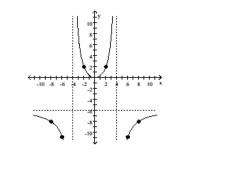
Find f(8).
A) 3
B) 8
C) -10.8
D) -8

Find f(8).
A) 3
B) 8
C) -10.8
D) -8
D
3
 Find the domain of the rational function.
Find the domain of the rational function.A) domain of
B) domain of
C) domain of
D) domain of
D
4
 Find the domain of the rational function.
Find the domain of the rational function.A) domain of
B) domain of
C) domain of
D) domain of

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
5
 Find the domain of the rational function.
Find the domain of the rational function.A) domain of
B) domain of
C) domain of
D) domain of

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
6
Find the function value.
A)
B) 2
C) 1
D)
A)
B) 2
C) 1
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the problem.
Suppose a cost-benefit model is given by , where is the cost in thousands of dollars for removing percent of a given pollutant. Find the cost for removing of the pollutant.
A) thousands
B) thousands
C) thousands
D) thousands
Suppose a cost-benefit model is given by , where is the cost in thousands of dollars for removing percent of a given pollutant. Find the cost for removing of the pollutant.
A) thousands
B) thousands
C) thousands
D) thousands

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
8
 Find the domain of the rational function.
Find the domain of the rational function.A) domain of
B) domain of
C) domain of
D) domain of

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the problem.
A drug is injected into a patient and the concentration of the drug is monitored. The drug's concentration, , in milligrams after hours is modeled by . Estimate the drug's concentration after 4 hours. (Round to the nearest hundredth.)
A)
B)
C)
D)
A drug is injected into a patient and the concentration of the drug is monitored. The drug's concentration, , in milligrams after hours is modeled by . Estimate the drug's concentration after 4 hours. (Round to the nearest hundredth.)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the problem.
To calculate the drug dosage for a child, a pharmacist may use the formula . The child's age is and the adult dosage is D. What is the dosage for an 3 -year old child if the adult dosage is 40 mg? (Round to the nearest tenth.)
A)
B)
C)
D)
To calculate the drug dosage for a child, a pharmacist may use the formula . The child's age is and the adult dosage is D. What is the dosage for an 3 -year old child if the adult dosage is 40 mg? (Round to the nearest tenth.)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
11
 Find the domain of the rational function.
Find the domain of the rational function.A) domain of
B) domain of
C) domain of
D) domain of

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
12
The graph of a rational function, f, is shown in the figure. Use the graph to answer the question. 
Find all horizontal asymptotes of the graph.
A) x = 4, x = -4
B) x = -6
C) y = -6
D) y = 4, y = -4

Find all horizontal asymptotes of the graph.
A) x = 4, x = -4
B) x = -6
C) y = -6
D) y = 4, y = -4

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
13
Find the function value.
A)
B) 4
C) 1
D) 3
A)
B) 4
C) 1
D) 3

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
14
Find the function value.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
15
The graph of a rational function, f, is shown in the figure. Use the graph to answer the question. 
Find f(-2).
A) 1
B) 0
C) -2
D) 2

Find f(-2).
A) 1
B) 0
C) -2
D) 2

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
16
 Find the domain of the rational function.
Find the domain of the rational function.A) domain of
B) domain of
C) domain of
D) domain of

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
17
Find the function value.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
18
 Find the domain of the rational function.
Find the domain of the rational function.A) domain of
B) domain of
C) domain of
D) domain of

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
19
The graph of a rational function, f, is shown in the figure. Use the graph to answer the question. 
Find all vertical asymptotes of the graph.
A) x = 4, x = -4
B) x = -6
C) y = 4, y = -4
D) y = -6

Find all vertical asymptotes of the graph.
A) x = 4, x = -4
B) x = -6
C) y = 4, y = -4
D) y = -6

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
20
Solve the problem.
A company that produces radios has costs given by the function C(x) = 25x + 25,000, where x is the number of radios manufactured and C(x) is measured in dollars. The average cost to manufacture each radio is given by . Find . (Round to the nearest dollar, if necessary.)
A)
B)
C)
D)
A company that produces radios has costs given by the function C(x) = 25x + 25,000, where x is the number of radios manufactured and C(x) is measured in dollars. The average cost to manufacture each radio is given by . Find . (Round to the nearest dollar, if necessary.)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
21
Simplify the rational expression. If the rational expression cannot be simplified, so state.
A)
B)
C)
D) Cannot be simplified
A)
B)
C)
D) Cannot be simplified

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
22
Simplify the rational expression. If the rational expression cannot be simplified, so state.
A)
B)
C)
D) Cannot be simplified
A)
B)
C)
D) Cannot be simplified

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
23
According to the cost model, is it possible to remove 100% of the trash from American highways?
A) Yes
B) No

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
24
Simplify the rational expression. If the rational expression cannot be simplified, so state.
A) Cannot be simplified
B)
C)
D)
A) Cannot be simplified
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
25
The graph of a rational function, f, is shown in the figure. Use the graph to answer the question. 
Is 4 a function value of f?
A) Yes
B) No

Is 4 a function value of f?
A) Yes
B) No

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
26
Multiply as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
27
The graph of a rational function, f, is shown in the figure. Use the graph to answer the question. 
How does the graph indicate that f(-4) does not exist?
A) There is a horizontal asymptote at x = -4 indicated by a dashed line.
B) There is a horizontal asymptote at y = -4 indicated by a dashed line.
C) There is a vertical asymptote at y = -4 indicated by a dashed line.
D) There is a vertical asymptote at x = -4 indicated by a dashed line.

How does the graph indicate that f(-4) does not exist?
A) There is a horizontal asymptote at x = -4 indicated by a dashed line.
B) There is a horizontal asymptote at y = -4 indicated by a dashed line.
C) There is a vertical asymptote at y = -4 indicated by a dashed line.
D) There is a vertical asymptote at x = -4 indicated by a dashed line.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
28
The graph of a rational function, f, is shown in the figure. Use the graph to answer the question. 
Is -3 a function value of f?
A) Yes
B) No

Is -3 a function value of f?
A) Yes
B) No

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
29
Simplify the rational expression. If the rational expression cannot be simplified, so state.
A)
B)
C)
D) Cannot be simplified
A)
B)
C)
D) Cannot be simplified

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
30
Simplify the rational expression. If the rational expression cannot be simplified, so state.
A) Cannot be simplified
B)
C)
D)
A) Cannot be simplified
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
31
Multiply as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
32
Simplify the rational expression. If the rational expression cannot be simplified, so state.
A)
B)
C)
D) Cannot be simplified
A)
B)
C)
D) Cannot be simplified

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
33
Use the equation to solve the problem. 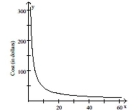
What is the horizontal asymptote of the graph? What does this mean about the cost to produce x bobble-heads?
A) y = 5; As the number of bobble-head figures produced increases, the cost is approaching $5.
B) y = 400; As the number of bobble-head figures produced increases, the cost is approaching $400.
C) There is no horizontal asymptote.
D) y = 0; As the number of bobble-head figures produced increases, the cost is approaching $0

What is the horizontal asymptote of the graph? What does this mean about the cost to produce x bobble-heads?
A) y = 5; As the number of bobble-head figures produced increases, the cost is approaching $5.
B) y = 400; As the number of bobble-head figures produced increases, the cost is approaching $400.
C) There is no horizontal asymptote.
D) y = 0; As the number of bobble-head figures produced increases, the cost is approaching $0

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
34
Simplify the rational expression. If the rational expression cannot be simplified, so state.
A)
B) Cannot be simplified
C)
D)
A)
B) Cannot be simplified
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
35
highways. The graph is shown. Use the equation to solve the problem. 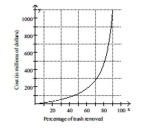
What value of x must be excluded from the rational function's domain?
A) 10
B) 100
C) 1000
D) 1

What value of x must be excluded from the rational function's domain?
A) 10
B) 100
C) 1000
D) 1

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
36
Use the equation to solve the problem. 
Find and interpret f(40).
A) 15; It costs $15 to produce 40 bobble-head figures.
B) 405; It costs $405 to produce 40 bobble-head figures.
C) 5; It costs $5 to produce 40 bobble-head figures.
D) 600; It costs $600 to produce 40 bobble-head figures.

Find and interpret f(40).
A) 15; It costs $15 to produce 40 bobble-head figures.
B) 405; It costs $405 to produce 40 bobble-head figures.
C) 5; It costs $5 to produce 40 bobble-head figures.
D) 600; It costs $600 to produce 40 bobble-head figures.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
37
Multiply as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
38
The graph of a rational function, f, is shown in the figure. Use the graph to answer the question. 
How can you tell that this is not the graph of a polynomial function?
A) The graph is not continuous.
B) The value of f(1) is not equal to 1.
C) The graph is continuous.
D) The graph is not a parabola.

How can you tell that this is not the graph of a polynomial function?
A) The graph is not continuous.
B) The value of f(1) is not equal to 1.
C) The graph is continuous.
D) The graph is not a parabola.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
39
highways. The graph is shown. Use the equation to solve the problem. 
Find and interpret f(80).
A) 48; The cost to remove 80% of the trash is $48 million.
B) 48; The cost to remove 20% of the trash is $48 million.
C) 48; The cost to remove 80% of the trash is $48 .
D) 20; The cost to remove 80% of the trash is $20 million.

Find and interpret f(80).
A) 48; The cost to remove 80% of the trash is $48 million.
B) 48; The cost to remove 20% of the trash is $48 million.
C) 48; The cost to remove 80% of the trash is $48 .
D) 20; The cost to remove 80% of the trash is $20 million.

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
40
Simplify the rational expression. If the rational expression cannot be simplified, so state.
A)
B)
C)
D) Cannot be simplified
A)
B)
C)
D) Cannot be simplified

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
41
Multiply as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
42
Divide as indicated.
A) 1
B)
C)
D)
A) 1
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
43
Divide as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
44
Multiply as indicated.
A)
C)
D)
A)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
45
Divide as indicated.
A)
B) 1
C) 18
D)
A)
B) 1
C) 18
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
46
Divide as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
47
Add. Simplify the result, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
48
Add. Simplify the result, if possible.
A) 3
B)
C)
D)
A) 3
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
49
Divide as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
50
Multiply as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
51
Multiply as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
52
Add. Simplify the result, if possible.
A)
B) 2
C)
D)
A)
B) 2
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
53
Divide as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
54
Divide as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
55
Multiply as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
56
Divide as indicated.
A)
B) 18
C)
D)
A)
B) 18
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
57
Divide as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
58
Multiply as indicated.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
59
Multiply as indicated.
A)
B)
C)
D) 1
A)
B)
C)
D) 1

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
60
Add. Simplify the result, if possible.
B) 1
C)
D)
A)
B) 1
C)
D)
A)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
61
Subtract. Simplify the result, if possible.
A)
B) 13
C)
D)
A)
B) 13
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
62
Subtract. Simplify the result, if possible.
A) 3
B)
C)
D)
A) 3
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
63
Perform the indicated operations. Simplify the result, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
64
Find the least common denominator of the rational expressions.
, and
A)
B)
C)
D)
, and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
65
Perform the indicated operations. Simplify the result, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
66
Subtract. Simplify the result, if possible.
A)
B)
C) 0
D)
A)
B)
C) 0
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
67
Find the least common denominator of the rational expressions.
and
A)
B)
C)
D)
and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
68
Find the least common denominator of the rational expressions.
, and
A)
B)
C)
D)
, and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
69
Find the least common denominator of the rational expressions.
and
A)
B)
C)
D)
and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
70
Perform the indicated operations. Simplify the result, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
71
Find the least common denominator of the rational expressions.
and
A)
B)
C)
D)
and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
72
Subtract. Simplify the result, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
73
Find the least common denominator of the rational expressions.
and
A)
B)
C)
D)
and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
74
Perform the indicated operations. Simplify the result, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
75
Find the least common denominator of the rational expressions.
and
A)
B) 6
C)
D)
and
A)
B) 6
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
76
Add. Simplify the result, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
77
Find the least common denominator of the rational expressions.
and
A)
B)
C)
D)
and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
78
Perform the indicated operations. Simplify the result, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
79
Perform the indicated operations. Simplify the result, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck
80
Add. Simplify the result, if possible.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 102 flashcards in this deck.
Unlock Deck
k this deck


